江西省鄱阳县八校2023年联考中考一模数学试题
试卷更新日期:2023-04-06 类型:中考模拟
一、单选题
-
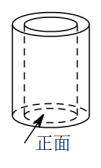
1. 下列各数中,是正数的是( )A、 B、0 C、2 D、2. 如图是一个空心圆柱体,其主视图是( )
 A、
A、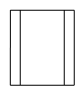 B、
B、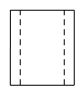 C、
C、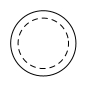 D、
D、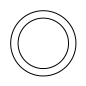 3. 下列结果中计算正确的是( )A、 B、 C、 D、4. 直线与直线相交于点 , 则的值为( )A、 B、5 C、7 D、85. 设 , 是方程的两个实数根,则的值为( )A、 B、 C、12 D、106. 已知 , 为抛物线上的点,且原点为的中点,则线段的长为( )A、 B、 C、 D、
3. 下列结果中计算正确的是( )A、 B、 C、 D、4. 直线与直线相交于点 , 则的值为( )A、 B、5 C、7 D、85. 设 , 是方程的两个实数根,则的值为( )A、 B、 C、12 D、106. 已知 , 为抛物线上的点,且原点为的中点,则线段的长为( )A、 B、 C、 D、二、填空题
-
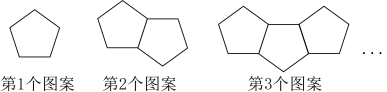
7. 据消息,2022年江西省研究生考试报名人数为14.07万,将数据14.07万用科学记数法表示为 .8. 正六边形的每个内角等于°.9. 如图所示的是由一些火柴棒摆成的图案:摆第1个图案用了5根火柴,摆第2个图案用了9根火柴,摆第3个图案用了13根火柴……按照这种方式摆下去,摆第10个图案需要用的火柴棒根数是 .
 10. 七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,经历代演变而成七巧板,如图1所示.19世纪传到国外,被称为“唐图”(意为“来自中国的拼图”),图2是由边长为4的正方形分割制作的七巧板拼摆而成的“叶问蹬”图,则图中抬起的“腿”(即阴影部分)的面积为 .
10. 七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,经历代演变而成七巧板,如图1所示.19世纪传到国外,被称为“唐图”(意为“来自中国的拼图”),图2是由边长为4的正方形分割制作的七巧板拼摆而成的“叶问蹬”图,则图中抬起的“腿”(即阴影部分)的面积为 .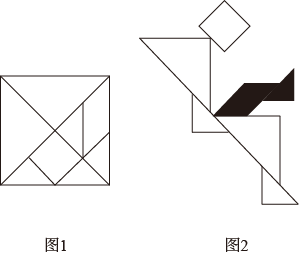 11. 如图,在正方形中,将边绕点逆时针旋转至 , 连接 , , 若 , , 则线段的长度为 .
11. 如图,在正方形中,将边绕点逆时针旋转至 , 连接 , , 若 , , 则线段的长度为 .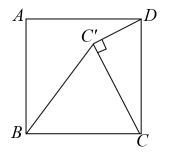 12. 如图, , 点在上,且 , 是上的点,在上找点 , 以为边, , , 为顶点作正方形,则的长为 .
12. 如图, , 点在上,且 , 是上的点,在上找点 , 以为边, , , 为顶点作正方形,则的长为 .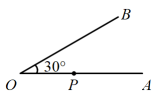
三、解答题
-
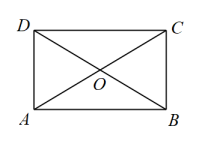
13. 计算:(1)、计算: .(2)、如图,在四边形中, , , 对角线 , 相交于点 , 且 . 求证:在四边形是矩形.
 14. 解不等式组: , 并把解集在数轴上表示出来.
14. 解不等式组: , 并把解集在数轴上表示出来.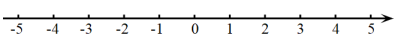 15. 如图,是正方形的边上一点,连接 . 请仅用无刻度的直尺完成画图.(保留画图痕迹,不写作法)
15. 如图,是正方形的边上一点,连接 . 请仅用无刻度的直尺完成画图.(保留画图痕迹,不写作法)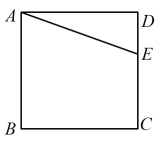 (1)、在边上找点 , 使得 .(2)、将线段绕点顺时针旋转90°,得到线段 , 画出 .16. 为了解学生最喜欢的球类运动,学校从九年级的学生中随机抽取了部分学生,进行问卷调查(每个被调查的学生在5种球类运动中只选择最喜欢的一种),5种球类运动分别是:A篮球,足球,排球,羽毛球,乒乓球.(1)、某学生选到足球的概率是 .(2)、学校想从4名学生(2名男生,2名女生)中随机抽取2名学生谈谈自己喜爱的原因.请用列表或画树状图的方法,求抽到的2名学生是一男一女的概率.17. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于 , 两点.
(1)、在边上找点 , 使得 .(2)、将线段绕点顺时针旋转90°,得到线段 , 画出 .16. 为了解学生最喜欢的球类运动,学校从九年级的学生中随机抽取了部分学生,进行问卷调查(每个被调查的学生在5种球类运动中只选择最喜欢的一种),5种球类运动分别是:A篮球,足球,排球,羽毛球,乒乓球.(1)、某学生选到足球的概率是 .(2)、学校想从4名学生(2名男生,2名女生)中随机抽取2名学生谈谈自己喜爱的原因.请用列表或画树状图的方法,求抽到的2名学生是一男一女的概率.17. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于 , 两点.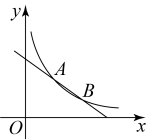 (1)、求点 , 的坐标.(2)、求一次函数与反比例函数的表达式.18. 为了解双减背景下学生每天完成作业的时间情况,某中学对名学生每天完成作业时间进行抽样调查,根据时间(单位:分钟)分成 , , , , 五个组,并将调查结果绘制成如图所示的两幅不完整的统计图.
(1)、求点 , 的坐标.(2)、求一次函数与反比例函数的表达式.18. 为了解双减背景下学生每天完成作业的时间情况,某中学对名学生每天完成作业时间进行抽样调查,根据时间(单位:分钟)分成 , , , , 五个组,并将调查结果绘制成如图所示的两幅不完整的统计图.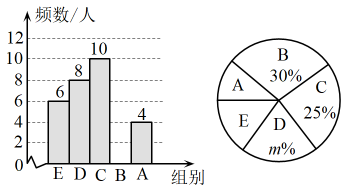
根据以上信息,回答下列问题:
(1)、n= , m= .(2)、学生每天完成作业时间的中位数落在组,众数落组.(3)、若全校共有名学生,请估计该校每天完成作业时间不低于120分钟的学生有多少人.19. 为创建国家卫生城市,我市计划将城市道路两旁的人行道进行改造.经调查可知,若该工程由甲工程队单独来做,恰好能在规定时间内完成.若该工程由乙工程队单独完成,则需要的天数是规定时间的3倍.若甲、乙两工程队合作3天后,余下的工程由甲工程队单独来做还需4天完成.(1)、问我市要求完成这项工程规定的时间是多少天?(2)、已知甲工程队做一天需付工资3万元,乙工程队做一天需付工资0.8万元.应该怎样安排才能在规定的时间完成这项工程,并使工程花费最少?最少是多少元?20. “垃圾入桶,保护环境从我做起”,如图所示的是某款垃圾桶侧面展示图, , , 桶盖可以绕点G逆时针方向旋转,当旋转角为时,桶盖落在的位置.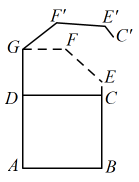 (1)、求在桶盖旋转过程中,点C运动轨迹的长度.(2)、求点到地面的距离.(参考数据:)21. 如图,以线段上一点为圆心,长为半径画圆,交于点 , 是上异于点 , 的一点. , 且 .
(1)、求在桶盖旋转过程中,点C运动轨迹的长度.(2)、求点到地面的距离.(参考数据:)21. 如图,以线段上一点为圆心,长为半径画圆,交于点 , 是上异于点 , 的一点. , 且 .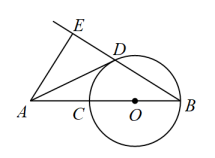 (1)、求证:是的切线.(2)、若 , 平分 , 求线段的长.22. 如图,抛物线与轴相交于点 , 与轴相交于点 .
(1)、求证:是的切线.(2)、若 , 平分 , 求线段的长.22. 如图,抛物线与轴相交于点 , 与轴相交于点 .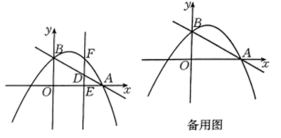 (1)、求抛物线的表达式.(2)、为线段上一点(不与点 , 重合),过点作轴于点 , 交抛物线于点 , 若 , 求点的坐标.(3)、是第四象限内抛物线上一点,已知 , 则点的坐标为 .23. 课本再现
(1)、求抛物线的表达式.(2)、为线段上一点(不与点 , 重合),过点作轴于点 , 交抛物线于点 , 若 , 求点的坐标.(3)、是第四象限内抛物线上一点,已知 , 则点的坐标为 .23. 课本再现如图1,在等边中,为边上一点,为上一点,且 , 连接与相交于点 .
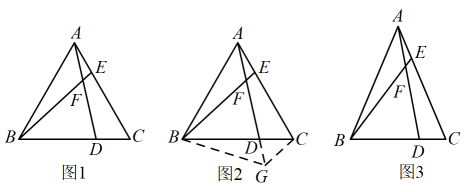 (1)、与的数量关系是 , 与构成的锐角夹角的度数是 .(2)、深入探究:将图1中的延长至点 , 使 , 连接 , , 如图2所示.求证:平分 . (第一问的结论,本问可直接使用)(3)、迁移应用:如图3,在等腰中, , , 分别是边 , 上的点,与相交于点 . 若 , 且 , 求的值.
(1)、与的数量关系是 , 与构成的锐角夹角的度数是 .(2)、深入探究:将图1中的延长至点 , 使 , 连接 , , 如图2所示.求证:平分 . (第一问的结论,本问可直接使用)(3)、迁移应用:如图3,在等腰中, , , 分别是边 , 上的点,与相交于点 . 若 , 且 , 求的值.