江西省南昌市青山湖区2023年九年级下学期3月质量调研数学试卷
试卷更新日期:2023-04-06 类型:中考模拟
一、单选题
-
1. 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图所示的几何体的左视图是( )
2. 如图所示的几何体的左视图是( )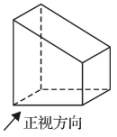 A、
A、 B、
B、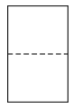 C、
C、 D、
D、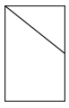 3. 已知点 , 均在反比例函数(k为常数)的图像上,若 , 则k的取值范围是( )A、 B、 C、 D、4. 某人在做抛掷硬币试验中,抛掷n次,正面朝上有m次,若正面朝上的频率是P= , 则下列说法正确的是( )A、P一定等于0.5 B、多投一次,P更接近0.5 C、P一定不等于0.5 D、投掷次数逐渐增加,P稳定在0.5附近5. 将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上,点A,B的读数分別为 , , 则的度数是( )
3. 已知点 , 均在反比例函数(k为常数)的图像上,若 , 则k的取值范围是( )A、 B、 C、 D、4. 某人在做抛掷硬币试验中,抛掷n次,正面朝上有m次,若正面朝上的频率是P= , 则下列说法正确的是( )A、P一定等于0.5 B、多投一次,P更接近0.5 C、P一定不等于0.5 D、投掷次数逐渐增加,P稳定在0.5附近5. 将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上,点A,B的读数分別为 , , 则的度数是( )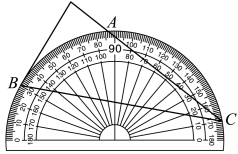 A、 B、 C、 D、6. 反比例函数 的图象如图所示,则二次函数y=2kx2﹣4x+k2的图象大致是( )
A、 B、 C、 D、6. 反比例函数 的图象如图所示,则二次函数y=2kx2﹣4x+k2的图象大致是( )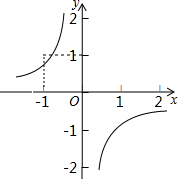 A、
A、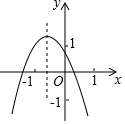 B、
B、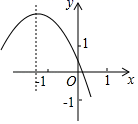 C、
C、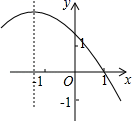 D、
D、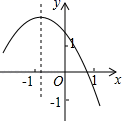
二、填空题
-
7. 在平面直角坐标系中,已知点与点关于原点对称,则 .8. 关于的一元二次方程有两个不同的实数根 , , 且 , 则 .9. 如图,中, , 将绕点顺时针旋转得到 , 若点正好在的延长线上,则的值为 .
 10. 《九章算术》记载了一个方程的问题,译文为:今有上禾6束,减损其中之“实”十八升,与下禾10束之“实“相当;下禾15束,减损其中之“实”五升,与上禾5束之“实”相当.问上、下禾每束之实各为多少升?设上、下禾每束之实各为x升和y升,则依题意可列方程组为 .11. 如图,在平面直角坐标中,菱形的顶点A在y轴的正半轴上,点B在函数的图象上,若 , 菱形的面积为 , 则k的值为 .
10. 《九章算术》记载了一个方程的问题,译文为:今有上禾6束,减损其中之“实”十八升,与下禾10束之“实“相当;下禾15束,减损其中之“实”五升,与上禾5束之“实”相当.问上、下禾每束之实各为多少升?设上、下禾每束之实各为x升和y升,则依题意可列方程组为 .11. 如图,在平面直角坐标中,菱形的顶点A在y轴的正半轴上,点B在函数的图象上,若 , 菱形的面积为 , 则k的值为 .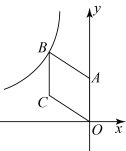 12. 在Rt△ABC纸片中,∠ACB=90°,AC=6,BC=8,P是AB边上一点,连接CP.沿CP把Rt△ABC纸片裁开,要使△ACP是等腰三角形,那么AP的长度是
12. 在Rt△ABC纸片中,∠ACB=90°,AC=6,BC=8,P是AB边上一点,连接CP.沿CP把Rt△ABC纸片裁开,要使△ACP是等腰三角形,那么AP的长度是三、解答题
-
13.(1)、;(2)、在中, , , 求的度数.14. 第24届北京冬奥会开幕式二十四节气倒计时惊艳亮相,从“雨水”开始,倒数最终行至“立春”,将中国人独有的浪漫传达给了全世界.李老师将每个节气的名称写在完全相同且不透明的小卡片上,洗匀后邀请同学随机抽取一张卡片,并向大家介绍卡片上对应节气的含义.(1)、若随机抽取一张卡片,则上面写有“立夏”的概率为;(2)、老师选出写有“立春、立夏、立秋、立冬”的四张卡片洗匀后背面朝上放在桌面上,请小星从中抽取一张卡片记下节气名称不放回,再洗匀后从中随机抽取一张卡片记下节气名称.请利用列表或画树状图的方法,求两次抽到的卡片上分别写有立春、立冬节气名称的概率.15. 美是一种感觉,当人体下半身长与身高的比值越接近时,越给人一种美感.如图,某女士身高 , 下半身长与身高的比值是 .
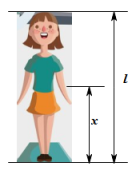 (1)、求该女士下半身长;(2)、为尽可能达到美的效果,求她应穿的高跟鞋的高度.(结果精确到)16. 如图,已知是的外接圆, , 请仅用无刻度的直尺,按下列要求画图(保留画图痕迹).
(1)、求该女士下半身长;(2)、为尽可能达到美的效果,求她应穿的高跟鞋的高度.(结果精确到)16. 如图,已知是的外接圆, , 请仅用无刻度的直尺,按下列要求画图(保留画图痕迹).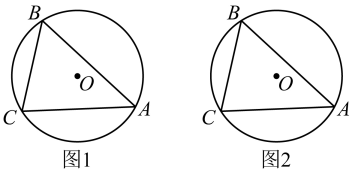 (1)、在图1的上作点D,使为等腰直角三角形;(2)、在图2的上作点M,N,使四边形为正方形.17. 沙漏又称“沙钟”,是我国古代一种计量时间的装置.它是根据均匀的沙粒从一玻璃球漏到另一个玻璃球的数量来计量时间.其中上面玻璃球中沙粒完全流入下面玻璃球后立即将沙漏倒置(倒置时间忽略不计),重新进行计时,周而复始.某课外数学小组观察发现:该沙漏上面玻璃球沙粒剩余量粒与流入时间秒成一次函数关系(不考虑其他因素),当流入时间在第秒时,上面玻璃球剩余沙粒粒,当流入时间在第秒时,上面玻璃球剩余沙粒粒.
(1)、在图1的上作点D,使为等腰直角三角形;(2)、在图2的上作点M,N,使四边形为正方形.17. 沙漏又称“沙钟”,是我国古代一种计量时间的装置.它是根据均匀的沙粒从一玻璃球漏到另一个玻璃球的数量来计量时间.其中上面玻璃球中沙粒完全流入下面玻璃球后立即将沙漏倒置(倒置时间忽略不计),重新进行计时,周而复始.某课外数学小组观察发现:该沙漏上面玻璃球沙粒剩余量粒与流入时间秒成一次函数关系(不考虑其他因素),当流入时间在第秒时,上面玻璃球剩余沙粒粒,当流入时间在第秒时,上面玻璃球剩余沙粒粒. (1)、求出上面玻璃球沙粒余量粒与流入时间(秒)之间的函数关系式;(2)、求沙漏恰好完成第一次倒置所需时间.18. 某中学积极落实国家“双减”教育政策,决定增设“礼仪”、“陶艺”、“园艺”、“厨艺”及“编程”等五门校本课程以提升课后服务质量,促进学生全面健康发展.学校面向七年级参与课后服务的部分学生开展了“你选修哪门课程?”(要求必须选修一门且只能选修一门)的随机问卷调查,并根据调查数据绘制了如下两幅不完整的统计图:请结合上述信息,解答下列问题:
(1)、求出上面玻璃球沙粒余量粒与流入时间(秒)之间的函数关系式;(2)、求沙漏恰好完成第一次倒置所需时间.18. 某中学积极落实国家“双减”教育政策,决定增设“礼仪”、“陶艺”、“园艺”、“厨艺”及“编程”等五门校本课程以提升课后服务质量,促进学生全面健康发展.学校面向七年级参与课后服务的部分学生开展了“你选修哪门课程?”(要求必须选修一门且只能选修一门)的随机问卷调查,并根据调查数据绘制了如下两幅不完整的统计图:请结合上述信息,解答下列问题: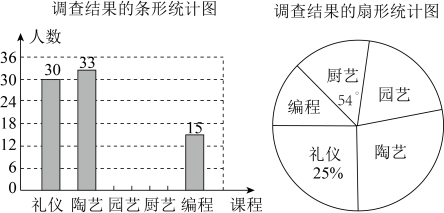 (1)、请补充条形统计图,并计算共有 ▲ 名学生参与了本次问卷调查;(2)、“陶艺”在扇形统计图中所对应的圆心角是度;(3)、若该校七年级共有550人,请你估计选修“园艺”的同学人数为多少?19. 如图,直线与反比例函数的图象交于点 , 与轴,轴依次交于点B,点C.
(1)、请补充条形统计图,并计算共有 ▲ 名学生参与了本次问卷调查;(2)、“陶艺”在扇形统计图中所对应的圆心角是度;(3)、若该校七年级共有550人,请你估计选修“园艺”的同学人数为多少?19. 如图,直线与反比例函数的图象交于点 , 与轴,轴依次交于点B,点C.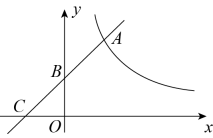 (1)、当时,求的值;(2)、判定与的比值能否与相等?若有,求线段的长度;若没有,请说明理由.20. 如图1是一座拱桥,图2是其侧面示意图,斜道的坡度 , 斜道的坡度 , 测得湖宽米,米,米,已知弧所在圆的圆心在上.(备注:坡度即坡角的正切值,如的坡度 . )
(1)、当时,求的值;(2)、判定与的比值能否与相等?若有,求线段的长度;若没有,请说明理由.20. 如图1是一座拱桥,图2是其侧面示意图,斜道的坡度 , 斜道的坡度 , 测得湖宽米,米,米,已知弧所在圆的圆心在上.(备注:坡度即坡角的正切值,如的坡度 . ) (1)、分别求拱桥部分C、D到直线的距离;(2)、求弧的长(结果保留π).21. 如图,是的外接圆,分别过A,C作 , .
(1)、分别求拱桥部分C、D到直线的距离;(2)、求弧的长(结果保留π).21. 如图,是的外接圆,分别过A,C作 , .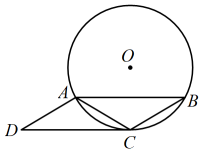 (1)、求证:;(2)、若 .
(1)、求证:;(2)、若 .①求证:是的切线;
②已知 , 当四边形的某条边所在直线过圆心O时,求的半径.
22. 为增强学生身体素质,创设体育文化氛围,某校开展田径运动会,小贤同学报了投铅球比赛的项目,如图曲线AB就是他投出的铅球运动路线,呈抛物线形,出手点A离地面的高度为 , 铅球飞行的水平距离的长度为m.过作于点 , 以OB为轴,为y轴,建立平面直角坐标系,如图所示.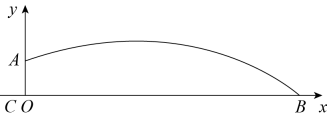 (1)、写出 , 两点的坐标;(2)、若抛物线的解析式为
(1)、写出 , 两点的坐标;(2)、若抛物线的解析式为①求的取值范围;
②若 , 求小贤同学投出的铅球运动路线(抛物线)的解析式.
23. 如图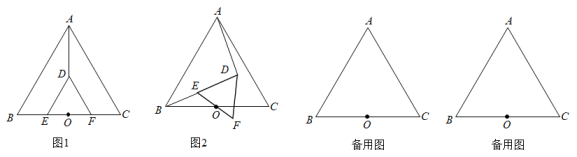 (1)、问题发现:
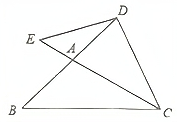
(1)、问题发现:如图1,和都是等边三角形,边和在同一直线上,是边的中点, , 连接 , 则下列结论正确的是 . (填序号即可)
①;②;③;④整个图形是轴对称图形.
(2)、数学思考:将图1中的绕着点旋转,不动,连接和 , 如图2,则和具有怎样的数量和位置关系?请给出证明过程;(3)、拓展应用:已知 , , 在图1中的绕着点旋转的过程中,当时,求线段的长度.