河北省石家庄新华区2023年九年级基础知识质量监测数学试题（3月模拟考）

试卷更新日期：2023-04-06 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图，从A地到B地的四条路线中，路程最短的是（）

A、1 B、2 C、3 D、4

查看试题解析
2. 中国是最早采用正负数表示相反意义的量，并进行负数运算的国家．在下列含有负数的运算中，运算结果是负数的为（）

A、 $(- 2) + (- 3)$ B、 $(- 2) - (- 3)$ C、 $(- 2) \times (- 3)$ D、 $(- 2) \div (- 3)$

查看试题解析
3. 下列整式与 $x^{2} y$ 为同类项的是（）

A、 $3 x y$ B、 $2 x^{2} y$ C、 $x^{2} y z$ D、 $- 5 x y^{2}$

查看试题解析
4. 一个正方形和一个直角三角形的位置如图所示，若 $∠ 1 = α$ ，则 $∠ 2 =$ （）

A、 $α - 45 °$ B、 $α - 90 °$ C、 $270 ° - α$ D、 $180 ° - α$

查看试题解析
5. 已知1纳米 $= 1 {0^{-}}^{9}$ 米，将 $\frac{1}{4}$ 纳米用科学记数法表示的结果是（）

A、 $0.25 \times 1 0^{- 8}$ 米 B、 $2.5 \times 1 0^{- 9}$ 米 C、 $2.5 \times 1 0^{- 10}$ 米 D、 $25 \times 1 0^{- 11}$ 米

查看试题解析
6. 将如图所示的长方体包装盒沿某些棱剪开，且使六个面连在一起，然后铺平，则得到的图形不可能是（）

A、 B、 C、 D、

查看试题解析
7. 已知 $a + 2 b - 3 = 0$ ，则 $2 a + 4 b + 6$ 的值是（）

A、8 B、12 C、18 D、24

查看试题解析
8. 如图，在 $4 \times 4$ 的正方形格纸中， $△ A B C$ 的顶点均在格点上， $B C$ 边与网格线交于点D， $A C$ 边过格点E，连接 $A D$ ， $B E$ 相交于点O，则点O为 $△ A B C$ 的（）

A、重心 B、外心 C、内心 D、以上结果均不对

查看试题解析
9. 从1，2，3，4这四个数中任选两个数，其和为奇数的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{3}{4}$ D、 $\frac{5}{6}$

查看试题解析
10. 若关于x的一元二次方程 $k x^{2} - 3 x - \frac{9}{4} = 0$ 有两个不相等的实数根，则整数k的最小值是（）

A、 $- 2$ B、 $- 1$ C、0 D、1

查看试题解析
11. 如图，在 $▱ A B C D$ 中，点E为 $B C$ 边的中点，按以下步骤作图：（1）以点E为圆心，任意长为半径画弧，分别交 $B C$ 于M、N两点；（2）分别以M、N两点为圆心，大于 $\frac{1}{2} M N$ 的长为半径画弧，两弧交于点P；（3）作射线 $E P$ 交 $B D$ 于点F，连接 $C F$ ．
则有：① $F B = F C$ ；② $E F = D F$ ；③ $∠ A D B = ∠ B C F$ ；④ $∠ A B D = ∠ C F D$ ．
在上面四个结论中，正确的个数为（）

A、4 B、3 C、2 D、1

查看试题解析
12. 在平面直角坐标系中，点 $A (3 ， n - 2)$ 是反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象上一点，已知点 $B (3 ， n)$ ， $C (n - 2 ， n)$ ，连接 $B C$ ，则下列说法错误的是（）

A、点C可能在反比例函数 $y = \frac{k}{x}$ 的图象上 B、直线 $B C$ 与反比例函数 $y = \frac{k}{x}$ 的图象必有一个交点 C、n的值不可能为2 D、在反比例函数 $y = \frac{k}{x}$ 图象的一个分支上，可能存在y随x的增大而减小

查看试题解析
13. 如图， $A B$ 是半圆O的直径，C、D、E三点依次在半圆O上，若 $∠ C = α$ ， $∠ E = β$ ，则 $α$ 与 $β$ 之间的关系是（）

A、 $α + β = 270 °$ B、 $α + β = 180 °$ C、 $β = α + 90 °$ D、 $β = \frac{1}{2} α + 90 °$

查看试题解析
14. 二次函数 $y = x^{2} - 2 x + n + 1$ 的图象经过点 $A (m - 1 ， y_{1})$ 和 $B (m ， y_{2})$ ．当 $y_{1} < y_{2}$ 时，m的取值范围为（）

A、 $m < 1$ B、 $m > \frac{3}{2}$ C、 $m > 2$ D、 $\frac{3}{2} < m < 2$

查看试题解析
15. 如图，已知点 $A (- 2 ， 3)$ ， $B (2 ， 1)$ ，当直线 $y = k x - k$ 与线段 $A B$ 有交点时，k的取值范围是（）

A、 $k \leq - 1$ B、 $k \geq 1$ C、 $k \leq - 1$ 或 $k \geq 1$ D、 $k \leq - 3$ 或 $k \geq \frac{1}{3}$

查看试题解析
16. 如图，在边长为3的正方形 $A B C D$ 中，点E在边 $A D$ 上，且 $D E = 1$ ． $△ B E F$ 是以E为直角顶点的等腰直角三角形， $E F ， B F$ 分别交 $C D$ 于点M，N，过点F作 $A D$ 的垂线交 $A D$ 的延长线于点G．连接 $D F$ ，则下列结论错误的是（）

A、 $E F = \sqrt{13}$ B、 $D F = 2 \sqrt{2}$ C、 $C N = \frac{3}{5}$ D、 $M N = \frac{5}{3}$

查看试题解析

二、填空题

17. 计算： $\frac{2 a}{a + 1}$ + $\frac{2}{a + 1}$ = ．

查看试题解析
18. 如图，以正五边形 $A B C D E$ 的一边 $A B$ 为边，在正五边形内作等边 $△ A B F$ ，连接 $C F ， D F ， E F$ ，则

(1)、 $D F 与 A B$ 是否垂直？．（填“是”或“否”）；

(2)、 $∠ D F E$ 的度数是．

查看试题解析
19. 如图1，把一张标准纸一次又一次对折，得到“2开”纸、“4开”纸、“8开”纸、“16开”纸、……．当标准纸的短边长为a时．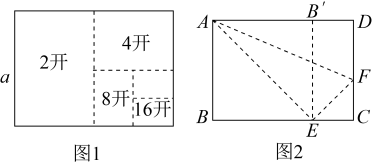

(1)、“16开”纸的短边长为（用含a的代数式表示）．

(2)、如图2，把这张标准纸对折得到的“16开”纸，按如下步骤折叠：
第一步，将矩形的短边 $A B$ 与长边 $A D$ 对齐折叠，点B落在 $A D$ 上的点 $B^{'}$ 处，铺平后得折痕 $A E$ ；
第二步，将长边 $A D$ 与折痕 $A E$ 对齐折叠，点D正好与点E重合，铺平后得折痕 $A F$ ．则：
①“16开”纸的长边长是（用含a的代数式表示）；
②标准纸的长边与短边的比值是．

查看试题解析

三、解答题

20. 已知二元一次方程：
① $x + y = 4$ ；
②2x—y＝2；
③x—2y＝1．
请你从这三个方程中选择你喜欢的两个方程，组成一个二元一次方程组，并求出它的解．

查看试题解析
21. 某校七、八年级各有500名学生，为了解这两个年级学生对2022年第24届北京冬奥会的关注程度，现从这两个年级各随机抽取m名学生进行冬奥会知识测试，并对测试成绩（满分100分，成绩取整数）进行整理和分析（成绩用x表示，单位：分）：分成四个组：甲： $80 \leq x < 85$ ；乙： $85 \leq x < 90$ ，丙： $90 \leq x < 95$ ；丁： $95 \leq x \leq 100$ ，并绘制了下列统计图（如图1和2所示）：
已知七年级在乙组中共有学生15人，他们的测试成绩分别为：85，85，85，86，87，87，87，88，88，88，89，89，89，88，88．请根据以上信息，完成下列问题：

(1)、 $m =$ ， $n =$ ；

(2)、七年级测试成绩的中位数是；

(3)、若测试成绩不低于90分，则认定该学生对冬奥会关注程度高．请估计该校七、八两个年级对冬奥会关注程度高的学生共有多少人？并说明理由．

查看试题解析
22. 设 $\bar{a 5}$ 是一个两位数，其中a是十位上的数字 $(1 \leq a \leq 9)$ ．例如，当 $a = 4$ 时， $\bar{a 5}$ 表示的两位数是45．

(1)、尝试：
①当 $a = 1$ 时， $1 5^{2} = 225 = 1 \times 2 \times 100 + 25$ ；
②当 $a = 2$ 时， $2 5^{2} = 625 = 2 \times 3 \times 100 + 25$ ；
③当 $a = 3$ 时， $3 5^{2} = 1225 =$ ；

(2)、归纳： $\bar{a 5^{2}} =$ ．

(3)、论证：请证明你归纳所得到的结论．

查看试题解析
23. 小明早晨从家里出发匀速步行去上学，小明的妈妈在小明出发后 $10 m i n$ ，发现小明的数学课本没带，于是她带上课本立即匀速骑车按小明上学的路线追赶小明，结果与小明同时到达学校，交接课本后立即按原路返回．已知小明距离家的路程 $s (k m)$ 与离开家的时间 $t (m i n)$ 之间的函数关系的图像如图所示．

(1)、求 $s (k m)$ 与 $t (m i n)$ 之间的函数关系；

(2)、请在图中画出小明的妈妈距离家的路程 $s (k m)$ 与小明离开家的时间 $t (m i n)$ 之间函数关系的图像；（备注：请对画出的图像用数据作适当的标注）

(3)、直接写出小明的妈妈在追赶小明及返回家的过程中，距学校 $0.5 k m$ 时 $t$ 的值．

查看试题解析
24. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A C = 3$ ， $B C = 4$ ． O为 $B C$ 边上一点，以O为圆心， $O B$ 为半径作半圆，分别于与边 $B C 、 A B$ 交于点D、E，连接 $D E$ ．

(1)、 $∠ B E D =$ °；

(2)、当 $B D = 3$ 时，求 $D E$ 的长；

(3)、过点E作半圆O的切线，当切线与边 $A C$ 相交时，设交点为F．求证： $A F = E F$ ．

查看试题解析
25. 如图，已知 $△ A B C$ 的面积 $S_{△ A B C} = 25$ ， $B C = 10$ ， M为 $A B$ 边上一动点（M与点A、B不重合），过点M作 $M N ∥ B C$ ，交 $A C$ 于点N，设 $M N = x$ ．

(1)、 $△ A B C$ 的边 $B C$ 的高 $h =$ ； $△ A M N$ 的面积 $S_{△ A M N} =$ （用含x的代数式表示）

(2)、把 $△ A M N$ 沿 $M N$ 折叠，设折叠后点A的对应点为 $A^{'}$ ， $△ A^{'} M N$ 与四边形 $B C N M$ 重叠部分的面积为y．
①求出y关于x的函数关系式，并写出自变量x的范围；
②当x为何值时重叠部分的面积y最大，最大值是多少？

查看试题解析
26. 在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $∠ C A B = 30 °$ ， $B C = 2$ ，将 $△ A B C$ 绕点C顺时针旋转，得到 $△ A_{1} B_{1} C_{1}$ ，连接 $A A_{1}$ ，设旋转角为 $α (0 ° < α < 360 °)$ ．

(1)、如图1，当 $A_{1} B_{1}$ 经过点B时，
①旋转角 $α =$ ▲ °；
②求证： $A_{1} B_{1} ⊥ A A_{1}$ ．

(2)、当 $A_{1} B_{1}$ 不经过点B时，连接 $B_{1} B$ 并延长 $B_{1} B$ 交直线 $A A_{1}$ 于点D，设 $A B$ 的中点为E， $B C$ 的中点为F．
①如图2，连接 $D E$ ，在 $△ A B C$ 的旋转过程中，线段 $D E$ 的长度有变化吗？如果有变化，请说明理由；如果不变，求 $D E$ 的值；
②如图3，连接 $D F$ ，直接写出 $D F$ 的最大值．

查看试题解析