河北省九地市2023年九年级摸底练习数学试题
试卷更新日期:2023-04-06 类型:中考模拟
一、单选题
-
1. 2023的相反数是( )A、 B、 C、 D、2. 从今年公布的全国第七次人口普查数据可知,湖北省人口约为5700万,其中5700万用科学记数法可表示为( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 如图,一束太阳光线平行照射在放置于地面的正六边形上,若 , 则的度数为( )
 A、 B、 C、 D、5. 下列运算或化简正确的是( )A、 B、 C、 D、6.
A、 B、 C、 D、5. 下列运算或化简正确的是( )A、 B、 C、 D、6.如图所示几何体的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 7. 式子可以化为( )A、 B、 C、 D、8. 如图,快艇从点A处向正北方向航行到B处时,向右转60°航行到C处,再向左转40°继续航行,此时的航行方向在点C的( )
7. 式子可以化为( )A、 B、 C、 D、8. 如图,快艇从点A处向正北方向航行到B处时,向右转60°航行到C处,再向左转40°继续航行,此时的航行方向在点C的( ) A、北偏东20° B、北偏西20° C、北偏东40° D、北偏西40°9. 已知点(﹣2,y1),(3,y2)都在直线y=﹣x﹣5上,则y1 , y2的值的大小关系是( )A、y1<y2 B、y1>y2 C、y1=y2 D、不能确定10. 语句“ 的 与 的和超过2”可以表示为( )A、 B、 C、 D、11. 连接正六边形不相邻的两个顶点,并将中间的六边形涂成黑色,制成如图所示的镖盘.将一枚飞镖任意投掷到镖盘上,飞镖落在黑色区域的概率为( )
A、北偏东20° B、北偏西20° C、北偏东40° D、北偏西40°9. 已知点(﹣2,y1),(3,y2)都在直线y=﹣x﹣5上,则y1 , y2的值的大小关系是( )A、y1<y2 B、y1>y2 C、y1=y2 D、不能确定10. 语句“ 的 与 的和超过2”可以表示为( )A、 B、 C、 D、11. 连接正六边形不相邻的两个顶点,并将中间的六边形涂成黑色,制成如图所示的镖盘.将一枚飞镖任意投掷到镖盘上,飞镖落在黑色区域的概率为( )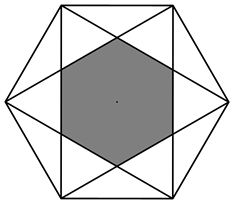 A、 B、 C、 D、12. 如图,中,点C为弦中点,连接 , , 点D是优弧上一点,则度数为( )
A、 B、 C、 D、12. 如图,中,点C为弦中点,连接 , , 点D是优弧上一点,则度数为( ) A、54° B、56° C、58° D、60°13. 如图,某梯子长10米,斜靠在竖直的墙面上,当梯子与水平地面所成角为 时,梯子顶端靠在墙面上的点 处,底端落在水平地面的点 处,现将梯子底端向墙面靠近,使梯子与地面所成角为 ,已知 ,则梯子顶端上升了( )
A、54° B、56° C、58° D、60°13. 如图,某梯子长10米,斜靠在竖直的墙面上,当梯子与水平地面所成角为 时,梯子顶端靠在墙面上的点 处,底端落在水平地面的点 处,现将梯子底端向墙面靠近,使梯子与地面所成角为 ,已知 ,则梯子顶端上升了( )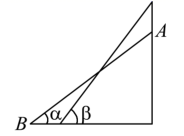 A、1米 B、1.5米 C、2米 D、2.5米14. 如图,为上任意一点,分别以、为边在同侧作正方形、正方形 , 设 , 则下列结论错误的是( )
A、1米 B、1.5米 C、2米 D、2.5米14. 如图,为上任意一点,分别以、为边在同侧作正方形、正方形 , 设 , 则下列结论错误的是( ) A、 B、 C、 D、15. 如图,在平面直角坐标系中,菱形的边与轴平行, , 两点纵坐标分别为 , , 反比例函数经过 , 两点,若 , 则值为( )
A、 B、 C、 D、15. 如图,在平面直角坐标系中,菱形的边与轴平行, , 两点纵坐标分别为 , , 反比例函数经过 , 两点,若 , 则值为( ) A、 B、 C、 D、16. 如图,在矩形ABCD中,点E从点B开始,沿矩形的边运动, , , 连接CE与对角线BD相交于点N,F是线段CE的中点,连接OF,则OF长度的最大值是( ).
A、 B、 C、 D、16. 如图,在矩形ABCD中,点E从点B开始,沿矩形的边运动, , , 连接CE与对角线BD相交于点N,F是线段CE的中点,连接OF,则OF长度的最大值是( ). A、1 B、 C、2 D、
A、1 B、 C、2 D、二、填空题
-
17. 已知关于x的一元二次方程有两个不相等的实数根,则实数m的取值范围是 .18. 如图,在中, , , , 将绕点A逆时针旋转角得到 , 并使点落在边上.
 (1)、旋转角的度数是 .(2)、线段所扫过部分的面积是为 . (结果保留)19. 如图, , 以为圆心,为半径作弧交于点 , 交于点 , 分别以点 , 为圆心,大于的长为半径画弧,两弧在的内部相交于点 , 画射线交于点 , 为上一动点,连接 , .
(1)、旋转角的度数是 .(2)、线段所扫过部分的面积是为 . (结果保留)19. 如图, , 以为圆心,为半径作弧交于点 , 交于点 , 分别以点 , 为圆心,大于的长为半径画弧,两弧在的内部相交于点 , 画射线交于点 , 为上一动点,连接 , . (1)、的度数是 .(2)、阴影部分周长的最小值为 .
(1)、的度数是 .(2)、阴影部分周长的最小值为 .三、解答题
-
20. 老师就式子 , 请同学们自己出问题并解答.(1)、小磊的问题:若代表 , 代表 , 计算该式的值.(2)、小敏的问题:若代表 , 代表 , 计算的结果是有理数,求有理数a的值.(3)、小捷的问题:若 , 且和所代表的数是互为相反数,直接写出所代表的数的取值范围.21. 小丽与小霞两位同学解方程的过程如下框:
小丽:
两边同除以 , 得 ,
解得 .
小霞:
移项,得 ,
提取公因式,得 .
所以或 ,
解得 , .
(1)、你认为他们的解法是否正确?若正确请在框内打“√”;若不正确请在框内打“×”,并写出你的解答过程.(2)、请结合上述题目总结:形如的一元二次方程的一般解法.22. 某学校举行了诗词知识竞赛,甲乙两班各派15名同学参加,现对甲、乙两班同学的分数进行整理分析如下:甲班15名同学的测试成绩(满分100分)统计如下:87,84,88,76,93,87,73,98,86,87,79,85,84,85,98.
乙班15名同学的测试成绩(满分100分)统计如下:77,88,92,85,76,90,76,91,88,81,85,88,98,86,89.
 (1)、按如表分数段整理两班测试成绩
(1)、按如表分数段整理两班测试成绩班级
70.5~75.5
75.5~80.5
80.5~85.5
85.5~90.5
90.5~95.5
95.5~100.5
甲
1
2
a
5
1
2
乙
0
3
3
6
2
1
表中 ;
(2)、补全甲班15名同学测试成绩的频数分布直方图;(3)、两班测试成绩的平均数、众数、中位数、方差如表所示:班级
平均数
众数
中位数
方差
甲
86
x
86
44.8
乙
86
88
y
36.7
表中 , .
(4)、你认为两班的测试成绩,较好的是 ▲ 班,为什么?23. 如图,已知是半圆O的直径, , 点D是线段延长线上的一个动点,直线垂直于射线于点D,在直线上选取一点C(点C在点D的上方),使 , 将射线绕点D逆时针旋转,旋转角为 . (1)、若 , 求点C与点O之间距离的最小值;(2)、当射线与相切于点C时,求劣弧的长度;24. 如图,一次函数的图象与x轴、y轴分别交于点A,B,与反比例函数的图象交于点 .
(1)、若 , 求点C与点O之间距离的最小值;(2)、当射线与相切于点C时,求劣弧的长度;24. 如图,一次函数的图象与x轴、y轴分别交于点A,B,与反比例函数的图象交于点 . (1)、直接写出不等式的解集;(2)、分别求出两个函数的解析式;(3)、连接 , 求的面积.
(1)、直接写出不等式的解集;(2)、分别求出两个函数的解析式;(3)、连接 , 求的面积.

