河北省保定市2023年中考一模考试数学卷
试卷更新日期:2023-04-06 类型:中考模拟
一、单选题
-
1. 若 , 则“□”是( )A、1 B、2 C、3 D、42. 下列图形中,称为扇形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列与相乘等于1的是( )A、 B、 C、 D、4. 若二次根式有意义,则x的取值范围在数轴上表示正确的是( )A、
3. 下列与相乘等于1的是( )A、 B、 C、 D、4. 若二次根式有意义,则x的取值范围在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,将折叠,使点落在边上处,展开后得到折痕 , 则是的( )
5. 如图,将折叠,使点落在边上处,展开后得到折痕 , 则是的( ) A、高 B、中线 C、中位线 D、角平分线6. 对于① , ② , 从左到右的变形,表述正确的是( )A、都是乘法运算 B、都是因式分解 C、①是乘法运算,②是因式分解 D、①是因式分解,②是乘法运算7. 如图,将矩形沿着裁剪得到一个四边形和一个三角形,设四边形的外角和与的外角和分别为 , 则( )
A、高 B、中线 C、中位线 D、角平分线6. 对于① , ② , 从左到右的变形,表述正确的是( )A、都是乘法运算 B、都是因式分解 C、①是乘法运算,②是因式分解 D、①是因式分解,②是乘法运算7. 如图,将矩形沿着裁剪得到一个四边形和一个三角形,设四边形的外角和与的外角和分别为 , 则( ) A、 B、 C、 D、无法比较与8. 如图,一个正方体骰子的六个面上分别标有1至6共六个数字,且相对面数字之和相同,将骰子按如图所示方式放置并按箭头方向无滑动翻转后停止在M处,则停止后骰子朝上面的数字为( )
A、 B、 C、 D、无法比较与8. 如图,一个正方体骰子的六个面上分别标有1至6共六个数字,且相对面数字之和相同,将骰子按如图所示方式放置并按箭头方向无滑动翻转后停止在M处,则停止后骰子朝上面的数字为( ) A、3 B、4 C、5 D、69. 射线的速度为光速的十分之一,若光速为 , 则射线的速度用科学记数法可表示为( )A、 B、 C、 D、10. 一种燕尾夹如图1所示,图2是在闭合状态时的示意图,图3是在打开状态时的示意图(此时),相关数据如图(单位:cm).从图2闭合状态到图3打开状态,点B,D之间的距离减少了( )
A、3 B、4 C、5 D、69. 射线的速度为光速的十分之一,若光速为 , 则射线的速度用科学记数法可表示为( )A、 B、 C、 D、10. 一种燕尾夹如图1所示,图2是在闭合状态时的示意图,图3是在打开状态时的示意图(此时),相关数据如图(单位:cm).从图2闭合状态到图3打开状态,点B,D之间的距离减少了( ) A、2cm B、3cm C、4cm D、5cm11. 在计算时,嘉嘉和琪琪使用方法不同,但计算结果相同,则( )
A、2cm B、3cm C、4cm D、5cm11. 在计算时,嘉嘉和琪琪使用方法不同,但计算结果相同,则( )嘉嘉:
琪琪:
A、嘉嘉正确 B、琪琪正确 C、都正确 D、都不正确12. 如图,平面直角坐标系中有M,N、P,Q四个点,其中的三个点在同一反比例函数的图象上,则不在这个图象上的点是( ) A、点N B、点M C、点P D、点Q13. 在如图所示的网格中,有两个完全相同的直角三角形纸片,如果把其中一个三角形纸片先横向平移格,再纵向平移格,就能使它的一条边与另一个三角形纸片的一条边重合,拼接成一个四边形,那么的结果( )
A、点N B、点M C、点P D、点Q13. 在如图所示的网格中,有两个完全相同的直角三角形纸片,如果把其中一个三角形纸片先横向平移格,再纵向平移格,就能使它的一条边与另一个三角形纸片的一条边重合,拼接成一个四边形,那么的结果( )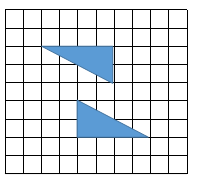 A、只有一个确定的值 B、有两个不同的值 C、有三个不同的值 D、有三个以上不同的值14. 水果店有一批大小不一的橘子,某顾客从中选购了个头大且均匀的橘子若干个,设原有橘子的重量的平均数和方差分别是 , 该顾客选购的橘子的重量的平均数和方差分别是 , 则下列结论一定成立的是( )A、 B、 C、 D、15. 如图所示的两个长方体容器中液体体积相同,根据图中信息,以下结论正确的是( )
A、只有一个确定的值 B、有两个不同的值 C、有三个不同的值 D、有三个以上不同的值14. 水果店有一批大小不一的橘子,某顾客从中选购了个头大且均匀的橘子若干个,设原有橘子的重量的平均数和方差分别是 , 该顾客选购的橘子的重量的平均数和方差分别是 , 则下列结论一定成立的是( )A、 B、 C、 D、15. 如图所示的两个长方体容器中液体体积相同,根据图中信息,以下结论正确的是( ) A、 B、 C、甲容器中液体的体积为405 D、乙容器中液面的高度为1016. 如图,在菱形中, , P为对角线上的一个动点,过点作的垂线,交或于点 , 交或于点 , 点从点出发以cm/s的速度向终点运动,设运动时间为 , 以为折线将菱形向右折叠,若重合部分面积为 , 求t的值,对于其答案,甲答: , 乙答: , 丙答: , 则正确的是( )
A、 B、 C、甲容器中液体的体积为405 D、乙容器中液面的高度为1016. 如图,在菱形中, , P为对角线上的一个动点,过点作的垂线,交或于点 , 交或于点 , 点从点出发以cm/s的速度向终点运动,设运动时间为 , 以为折线将菱形向右折叠,若重合部分面积为 , 求t的值,对于其答案,甲答: , 乙答: , 丙答: , 则正确的是( ) A、只有甲答的对 B、甲、乙答案合在一起才完整 C、甲、丙答案合在一起才完整 D、三人答案合在一起才充整
A、只有甲答的对 B、甲、乙答案合在一起才完整 C、甲、丙答案合在一起才完整 D、三人答案合在一起才充整二、填空题
-
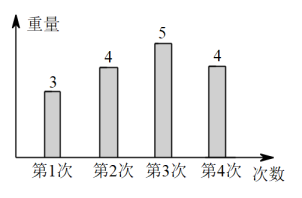
17. 如图所示的是莉莉次购买某水果的重量(单位,)的统计图,则次重量的中位数是 .
 18. 小颖将图1所示七巧板的其中几块拼成如图2所示的一个四边形 .
18. 小颖将图1所示七巧板的其中几块拼成如图2所示的一个四边形 . (1)、 .(2)、四边形的最长边长与最短边长的比值为 .19. 如图1,A,B,C是数轴上从左到右排列的三点,在数轴上对应的数分别为 , b,3,某同学将刻度尺按图2方式放置,使刻度尺上的数字0对齐数轴上的点A,发现点B对齐刻度尺处,点C对齐刻度尺处.(1)、在图1的数轴上,个单位长度.(2)、数轴上点B所对应的数b为 , 一质点P从点C处向点B方向跳动,第一次跳动到的中点处,第二次从点跳动到的中点处,第三次从点跳动到的中点处,如此跳动下去,则第四次跳动后,数轴上点所表示数为 .
(1)、 .(2)、四边形的最长边长与最短边长的比值为 .19. 如图1,A,B,C是数轴上从左到右排列的三点,在数轴上对应的数分别为 , b,3,某同学将刻度尺按图2方式放置,使刻度尺上的数字0对齐数轴上的点A,发现点B对齐刻度尺处,点C对齐刻度尺处.(1)、在图1的数轴上,个单位长度.(2)、数轴上点B所对应的数b为 , 一质点P从点C处向点B方向跳动,第一次跳动到的中点处,第二次从点跳动到的中点处,第三次从点跳动到的中点处,如此跳动下去,则第四次跳动后,数轴上点所表示数为 .
三、解答题
-
20. 整式的值为 .(1)、若的值为 , 求的值.(2)、若为非负数,求的取值范围.21. 亮亮和爸爸搭乘飞机外出游玩.若航班售票系统随机分配座位,且系统已将两人分配到同一排.如图所示的是飞机内同一排座位的排列示意图,
窗
过道
窗
(1)、求亮亮被分配到靠窗座位的概率;(2)、求亮亮和爸爸被分配到相邻座位的概率(过道两侧座位不算相邻).22. 灵活运用完全平方公式可以解决许多数学问题.例如:已知 , 求的值.
解: , ∴ ,
.
请根据以上材料,解答下列问题.
(1)、若与互为相反数,求的值.(2)、如图,矩形的长为a,宽为b,周长为14,面积为8,求的值.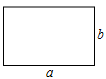 23. 如图,抛物线经过 , 两点,与轴交于点和点 .
23. 如图,抛物线经过 , 两点,与轴交于点和点 . (1)、求抛物线的解析式.(2)、将抛物线向右平移,使得点移至点处,求抛物线平移的距离.24. “垃圾入桶,保护环境从我做起”,如图所示的是某款垃圾桶侧面展示图, , , 桶盖可以绕点G逆时针方向旋转,当旋转角为时,桶盖落在的位置.
(1)、求抛物线的解析式.(2)、将抛物线向右平移,使得点移至点处,求抛物线平移的距离.24. “垃圾入桶,保护环境从我做起”,如图所示的是某款垃圾桶侧面展示图, , , 桶盖可以绕点G逆时针方向旋转,当旋转角为时,桶盖落在的位置.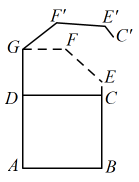 (1)、求在桶盖旋转过程中,点C运动轨迹的长度.(2)、求点到地面的距离.(参考数据:)25. 如图,在平面直角坐标系中,一次函数(m为常数)的图象交y轴于点 , 交x轴于点C,点A的坐标为 , 过点A作 , 且 , 连接 .
(1)、求在桶盖旋转过程中,点C运动轨迹的长度.(2)、求点到地面的距离.(参考数据:)25. 如图,在平面直角坐标系中,一次函数(m为常数)的图象交y轴于点 , 交x轴于点C,点A的坐标为 , 过点A作 , 且 , 连接 . (1)、求m的值和点D的坐标.(2)、求直线的解析式.(3)、东东设计了一个小程序:动点P从点D出发在线段上向点A运动,速度为每秒2个单位长度,同时动点Q从点B出发在线段上向点C运动,速度为每秒个单位长度,点Q到达点C后程序结束,设程序运行时间为t秒,当与四边形的边平行时程序会发出警报声,求发出警报声时t的值.26. 在矩形中, , , 将矩形绕点B顺时针旋转得到矩形 , A,C,D的对应点分别为 , , .
(1)、求m的值和点D的坐标.(2)、求直线的解析式.(3)、东东设计了一个小程序:动点P从点D出发在线段上向点A运动,速度为每秒2个单位长度,同时动点Q从点B出发在线段上向点C运动,速度为每秒个单位长度,点Q到达点C后程序结束,设程序运行时间为t秒,当与四边形的边平行时程序会发出警报声,求发出警报声时t的值.26. 在矩形中, , , 将矩形绕点B顺时针旋转得到矩形 , A,C,D的对应点分别为 , , . (1)、当点落在线段上时,完成以下探究.
(1)、当点落在线段上时,完成以下探究.①如图1,求的长.
②如图2,延长交于点E,求证: .
(2)、如图3,以为斜边在右侧作等腰直角三角形 , , 交于点G,交于点H,若 , 求的长.(3)、如图4,矩形的对角线与相交于点P,连接 , , 则面积的最小值为 .