广东省深圳市盐田区2023年九年级数学13校联考中考模拟试题

试卷更新日期：2023-04-06 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图是某几何体的三视图，则该几何体是（）

A、圆锥 B、圆柱 C、三棱柱 D、三棱锥

查看试题解析
2. 2021年5月，由中国航天科技集团研制的天问一号探测器的着陆巡视器成功着陆于火星乌托邦平原南部预选着陆区，中国航天器首次奔赴火星，就“毫发未损”地顺利出现在遇远的红色星球上，完成了人类航天史上的一次壮举．火星与地球的最近距离约为5500万千米，该数据用科学记数法可表示为（）千米

A、5.5×10⁸ B、5.5×10⁷ C、0.55×10⁹ D、0.55×10⁸

查看试题解析
3. 计算： $- \frac{1}{2}$ a²b·（ab）^-¹＝（）

A、 $\frac{1}{2}$ a B、 $\frac{1}{2}$ a³b² C、 $- \frac{1}{2}$ a D、 $- \frac{1}{2}$ a³b²

查看试题解析
4. 如图，直线l₁∥l₂ ，直线l₁、l₂被直线l₃所截，若∠1＝54°，则∠2的大小为（）

A、36° B、46° C、126° D、136°

查看试题解析
5. 如图， $Δ A B C$ 的中线 $B E$ 、 $C F$ 交于点 $O$ ，连接 $E F$ ，则 $\frac{O F}{F C}$ 的值为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{1}{4}$

查看试题解析
6. 新冠疫情防控形势下，学校要求学生每日测量体温．某同学连续一周的体温情况如表所示，则该同学这一周的体温数据的众数和中位数分别是（）
日期
星期一
星期二
星期三
星期四
星期五
星期六
星期天
体温（℃）
36.3
36.7
36.2
36.3
36.2
36.4
36.3

A、36.3和36.2 B、36.2和36.3 C、36.3和36.3 D、36.2和36.1

查看试题解析
7. 已知关于x的分式方程 $\frac{2 x + m}{x - 2}$ ＝3的解是x＝3，则m的值为（）

A、3 B、-3 C、-1 D、1

查看试题解析
8. 如图，在△ABC中，∠BAC＝70°，∠C＝40°，分别以点A和点C为圆心，大于 $\frac{1}{2}$ AC的长为半径画弧，两弧相交于点M，N，作直线MN交BC于点D，连接AD，则∠BAD的大小为（）

A、30° B、40° C、50° D、60°

查看试题解析
9. 如图， $A B$ 是 $⊙ O$ 的直径， $B C$ 是 $⊙ O$ 的弦，先将 $\overset{⌢}{B C}$ 沿 $B C$ 翻折交 $A B$ 于点 $D$ .再将 $\overset{⌢}{B D}$ 沿 $A B$ 翻折交 $B C$ 于点 $E$ .若 $\overset{⌢}{B E} = \overset{⌢}{D E}$ ，设 $∠ A B C = α$ ，则 $α$ 所在的范围是（）

A、 $21.9 ° < α < 22.3 °$ B、 $22.3 ° < α < 22.7 °$ C、 $22.7 ° < α < 23.1 °$ D、 $23.1 ° < α < 23.5 °$

查看试题解析
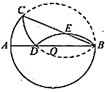10. 二次函数y＝ax²＋bx＋c的图象如图所示，下列说法错误的是（）

A、a＜0，b＞0 B、b²-4ac＞0 C、方程ax²＋bx＋c＝0的解是x₁＝5，x₂＝-1 D、不等式ax²＋bx＋c＞0的解集是0＜x＜5

查看试题解析

二、填空题

11. 分解因式： $4 x^{2} - 16$ = ．

查看试题解析
12. 已知方程 $x^{2} - 2 x - 8 ＝ 0$ 的两根为 $α 、 β$ ，则 $α^{2} + β^{2} ＝$ ．

查看试题解析
13. 我国古代数学家赵爽巧妙地用“弦图”证明了勾股定理，标志着中国古代的数学成就．如图所示的“弦图”，是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形．直角三角形的斜边长为13，一条直角边长为12，则小正方形ABCD的面积的大小为．

查看试题解析
14. 若点 $A (a ， 3)$ 、 $B (5 a ， b)$ 在同一个反比例函数的图象上，则 $b$ 的值为.

查看试题解析
15. 如图，在Rt△ABC中，∠C＝90°，∠B＝30°，AB＝8．若E、F是BC边上的两个动点，以EF为边的等边△EFP的顶点P在△ABC内部或边上，则等边△EFP的周长的最大值为．

查看试题解析

三、解答题

16. 计算： $(1 - π)^{0} - 2 c o s 30 ° + | - \sqrt{3} | - (\frac{1}{4})^{- 1}$ ．

查看试题解析
17. 先化简，再求值 $(1 + \frac{4}{x - 3}) \div \frac{x^{2} + 2 x + 1}{2 x - 6}$ ，其中 $x = \sqrt{2} - 1$ ．

查看试题解析
18. 钓鱼岛及其附属岛屿是中国的固有领土，神圣不可侵犯！自2021年2月1日起，旨在维护国家主权、更好履行海警机构职责的《中华人民共和国海警法》正式实施．中国海警在钓鱼岛海域开展巡航执法活动，是中方依法维护主权的正当举措．如图是钓鱼岛其中一个岛礁，若某测量船在海面上的点D处测得与斜坡AC坡脚点C的距离为140米，测得岛礁顶端A的仰角为30.96°，以及该斜坡AC的坡度i＝ $\frac{5}{6}$ ，求该岛礁的高（即点A到海平面的铅垂高度）．（结果保留整数）（参考数据：sin30.96°≈0.51，cos30.96°≈0.85，tan30.96°≈0.60）

查看试题解析
19. 如图，AB为⊙O的直径，C为BA延长线上一点，D为⊙O上一点，OF⊥AD于点E，交CD于点F，且∠ADC＝∠AOF．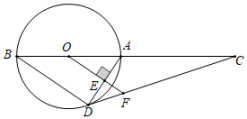

(1)、求证：CD与⊙O相切于点D；

(2)、若sin∠C＝ $\frac{1}{3}$ ， BD＝12，求EF的长．

查看试题解析
20. 某商家准备销售一种防护品，进货价格为每件50元，并且每件的售价不低于进货价．经过市场调查，每月的销售量y（件）与每件的售价x（元）之间满足如图所示的函数关系．

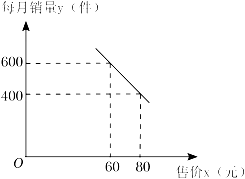(1)、求每月的销售量y（件）与每件的售价x（元）之间的函数关系式；（不必写出自变量的取值范围）

(2)、物价部门规定，该防护品每件的利润不允许高于进货价的30%．设这种防护品每月的总利润为w（元），那么售价定为多少元可获得最大利润？最大利润是多少？

查看试题解析
21. 某公园内人工湖上有一座拱桥（横截面如图所示），跨度AB为4米．在距点A水平距离为d米的地点，拱桥距离水面的高度为h米．小红根据学习函数的经验，对d和h之间的关系进行了探究．
下面是小红的探究过程，请补充完整：

(1)、经过测量，得出了d和h的几组对应值，如下表．
d/米
0
0.6
1
1.8
2.4
3
3.6
4
h/米
0.88
1.90
2.38
2.86
2.80
2.38
1.60
0.88
在d和h这两个变量中，是自变量，是这个变量的函数；

(2)、在下面的平面直角坐标系 $x O y$ 中，画出（1）中所确定的函数的图象；

(3)、结合表格数据和函数图象，解决问题：
①桥墩露出水面的高度AE为米；
②公园欲开设游船项目，现有长为3.5米，宽为1.5米，露出水面高度为2米的游船．为安全起见，公园要在水面上的C，D两处设置警戒线，并且 $C E = D F$ ，要求游船能从C，D两点之间安全通过，则C处距桥墩的距离CE至少为米．（精确到0.1米）

查看试题解析
22.

(1)、如图1， $R t △ A B C$ 中， $∠ C = 90 °$ ， $A B = 10$ ， $A C = 8$ ， $E$ 是 $A C$ 上一点， $A E = 5$ ， $E D ⊥ A B$ ，垂足为 $D$ ，求 $A D$ 的长．

(2)、类比探究：如图2， $△ A B C$ 中， $A C = 14$ ， $B C = 6$ ，点 $D$ ， $E$ 分别在线段 $A B$ ， $A C$ 上， $∠ E D B = ∠ A C B = 60 °$ ， $D E = 2$ ．求 $A D$ 的长．

(3)、拓展延伸：如图3， $△ A B C$ 中，点 $D$ ，点 $E$ 分别在线段 $A B$ ， $A C$ 上， $∠ E D B = ∠ A C B = 60 °$ ．延长 $D E$ ， $B C$ 交于点 $F$ ， $A D = 4$ ， $D E = 5$ ， $E F = 6$ ， $D E < B D$ ， $\frac{B C}{A C} =$ ， $B D =$ ．

查看试题解析

日期	星期一	星期二	星期三	星期四	星期五	星期六	星期天
体温（℃）	36.3	36.7	36.2	36.3	36.2	36.4	36.3

d/米	0	0.6	1	1.8	2.4	3	3.6	4
h/米	0.88	1.90	2.38	2.86	2.80	2.38	1.60	0.88