广东省深圳市南山区2023年九年级下学期第一次模拟考试数学试卷
试卷更新日期:2023-04-06 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 下列图形不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 疫情以后,为了保证大家的健康,学校对所有进入校园的师生进行体温检测,其中7名学生的体温(单位:)如下: , , , , , , . 这组数据的中位数是( )A、 B、 C、 D、4. 今年1月,深圳召开全市高质量发展大会,同时举行首批266个重大项目开工活动,预计本年度计划投资约535.6亿元,以高质量投资助力高质量发展.亿用科学记数法表示( )A、 B、 C、 D、5. 如图,往一个密封的正方体容器持续注入一些水,注水的过程中,可将容器任意放置,水平面形状不可能是( )
3. 疫情以后,为了保证大家的健康,学校对所有进入校园的师生进行体温检测,其中7名学生的体温(单位:)如下: , , , , , , . 这组数据的中位数是( )A、 B、 C、 D、4. 今年1月,深圳召开全市高质量发展大会,同时举行首批266个重大项目开工活动,预计本年度计划投资约535.6亿元,以高质量投资助力高质量发展.亿用科学记数法表示( )A、 B、 C、 D、5. 如图,往一个密封的正方体容器持续注入一些水,注水的过程中,可将容器任意放置,水平面形状不可能是( ) A、三角形 B、正方形 C、六边形 D、七边形6. 下列运算正确的是( )A、 B、 C、 D、7. 一副三角形板如图放置, , , , , 则的度数为( )
A、三角形 B、正方形 C、六边形 D、七边形6. 下列运算正确的是( )A、 B、 C、 D、7. 一副三角形板如图放置, , , , , 则的度数为( )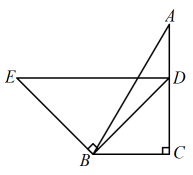 A、 B、 C、 D、8. 如图,已知 . 现按如下步骤作图:①以为圆心,以任意长为半径画弧,分别交于 , ;②分别以 , 为圆心,以大于长为半径画弧,两弧交于点 , 连接交于;③以为圆心,长为半径画弧,交于点;④以为圆心,长为半径画弧,交前弧于点;⑤作射线交OA于点I.若测得 , 则点E到的距离为( )
A、 B、 C、 D、8. 如图,已知 . 现按如下步骤作图:①以为圆心,以任意长为半径画弧,分别交于 , ;②分别以 , 为圆心,以大于长为半径画弧,两弧交于点 , 连接交于;③以为圆心,长为半径画弧,交于点;④以为圆心,长为半径画弧,交前弧于点;⑤作射线交OA于点I.若测得 , 则点E到的距离为( ) A、 B、3 C、 D、9. 华罗庚说过:“数形结合百般好,隔裂分家万事非.”请运用这句话中提到的思想方法判断方程的根的情况是( )A、有三个实数根 B、有两个实数根 C、有一个实数根 D、无实数根10. 如图,在边长为正方形中,点在以为圆心的弧上,射线交于 , 连接 , 若 , 则=( )
A、 B、3 C、 D、9. 华罗庚说过:“数形结合百般好,隔裂分家万事非.”请运用这句话中提到的思想方法判断方程的根的情况是( )A、有三个实数根 B、有两个实数根 C、有一个实数根 D、无实数根10. 如图,在边长为正方形中,点在以为圆心的弧上,射线交于 , 连接 , 若 , 则=( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 按照下图所示的操作步骤,若输入x的值为-2,则输出的值为.
 12. 一个二次二项式分解后其中的一个因式为 , 请写出一个满足条件的二次二项式 .13. 如图,AC经过⊙O的圆心O , AB与⊙O相切于点B , 若∠A=50°,则∠C=度.
12. 一个二次二项式分解后其中的一个因式为 , 请写出一个满足条件的二次二项式 .13. 如图,AC经过⊙O的圆心O , AB与⊙O相切于点B , 若∠A=50°,则∠C=度. 14. 如图,直角坐标系原点为斜边的中点, , 点坐标为 , 且 , 反比例函数经过点C,则k的值为 .
14. 如图,直角坐标系原点为斜边的中点, , 点坐标为 , 且 , 反比例函数经过点C,则k的值为 .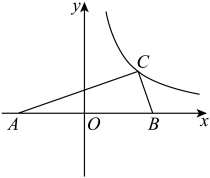 15. 如图,等边三角形边长为2,点D在边上,且 , 点E在边上且 , 连接 , 交于点F,在线段上截取 , 连接 , 则线段的最小值是 .
15. 如图,等边三角形边长为2,点D在边上,且 , 点E在边上且 , 连接 , 交于点F,在线段上截取 , 连接 , 则线段的最小值是 .
三、解答题
-
16. 解不等式组 , 并把解集在数轴上表示出来.
 17.(1)、直接写出结果计算: .(2)、利用(1)中的结论化简 .18. 为调查某校关于国家规定“中小学生每天在校体育活动时间不低于1h”的落实情况,某部门就“每天在校体育活动时间”随机调查了该校部分学生,根据调查结果绘制成如下不完整的统计图表.
17.(1)、直接写出结果计算: .(2)、利用(1)中的结论化简 .18. 为调查某校关于国家规定“中小学生每天在校体育活动时间不低于1h”的落实情况,某部门就“每天在校体育活动时间”随机调查了该校部分学生,根据调查结果绘制成如下不完整的统计图表.每天在校体育活动时间扇形统计图:

每天在校体育活动时间频数分布表:
组别
每天在校体育活动时间t/h
人数
A
t<0.5h
20
B
0.5h≤t<1h
40
C
1h≤t<1.5h
a
D
t≥1.5h
20
请根据以上图表信息,解答下列问题:
(1)、本次调查的学生共有人,a= , C组所在扇形的圆心角的大小是;(2)、若该校约有1500名学生,请估计其中达到国家规定体育活动时间的学生人数.19. “双减政策”要求学校更注重“减负增效”,学校为了保护学生的视力,倡导学生购买护眼灯.某商场为了保证供应充足,购进两种不同类型的护眼灯,若用3120元购进A型护眼灯的数量和用4200元购进B型护眼灯的数量相同,其中每台A型护眼灯比B型护眼灯便宜9元.(1)、求该商场购进每台A型和B型护眼灯的成本价.(2)、该商场经过调查发现,A型护眼灯售价为36元时,可以卖出100台.每涨价1元,则每天少售出2台.求每台A型护眼灯升价多少元时,销售利润最大?20.(1)、如图1,纸片中, , , 过点A作 , 垂足为E,沿剪下 , 将它平移至的位置,拼成四边形 , 则四边形的形状为____.(从以下选项中选取) A、正方形 B、菱形 C、矩形(2)、如图2,在(1)中的四边形纸片中,在上取一点F,使 , 剪下 , 将它平移至的位置,拼成四边形 .
A、正方形 B、菱形 C、矩形(2)、如图2,在(1)中的四边形纸片中,在上取一点F,使 , 剪下 , 将它平移至的位置,拼成四边形 .
①求证:四边形是菱形;
②连接 , 求的值.
21. 如图,抛物线与x轴交于 , 两点,与轴交于点 .

图1 备用图
(1)、求抛物线的解析式;(2)、如图1,是上方抛物线上一点,连接交线段于点 , 若 , 求点的坐标;(3)、抛物线上是否存在点使得 , 如果存在,请求出点的坐标,如果不存在,请说明理由.22. 在正方形中,点是对角线上的动点(与点 , 不重合),连接 . (1)、将射线绕点顺时针旋转 , 交直线于点 .
(1)、将射线绕点顺时针旋转 , 交直线于点 .①依题意补全图1;
②小深通过观察、实验,发现线段存在以下数量关系:的平方和等于的平方.小深把这个猜想与同学们进行交流,通过讨论,形成证明该猜想的几种想法:
想法1:将线段绕点逆时针旋转 , 得到线段 , 要证的关系,只需证的关系.
想法2:将沿翻折,得到 , 要证的关系,只需证的关系.
…
请你参考上面的想法,用等式表示线段的数量关系并证明;(一种方法即可)
(2)、如图2,若将直线绕点B顺时针旋转 , 交直线于点 . 若正方形边长为 , , 求的长.