广东省深圳市南山区2023年九年级数学十校联考数学试卷
试卷更新日期:2023-04-06 类型:中考模拟
一、单选题
-
1. 如图,该几何体的左视图是( )
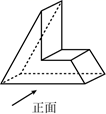 A、
A、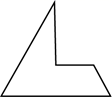 B、
B、 C、
C、 D、
D、 2. 国家卫健委网站消息:截至2022年5月27日,31个省(自治区,直辖市)和新疆生产建设兵团累计报告接种新冠病毒疫苗超过33亿剂次,用科学记数法表示33亿是( )A、 B、 C、 D、3. “天宫课堂”第二课3月23日在中国空间站开讲,包括六个项目:太空“冰雪”实验、液桥演示实验、水油分离实验、太空抛物实验、空间科学设施介绍与展示、天地互动环节.若随机选取一个项目写观后感,则恰好选到“实验”项目的概率是( )A、 B、 C、 D、4. 下列算式中,正确的是( )A、 B、 C、 D、5. 超市货架上有一批大小不一的鸡蛋,某顾客从中选购了部分大小均匀的鸡蛋,设货架上原有鸡蛋的质量(单位:g)平均数和方差分别为 , s2 , 该顾客选购的鸡蛋的质量平均数和方差1 , , 则下列结论一定成立的是( )A、1 B、1 C、s2> D、s26. 实数a在数轴上的对应点的位置如图所示.若实数 满足 ,则b的值可以是( )
2. 国家卫健委网站消息:截至2022年5月27日,31个省(自治区,直辖市)和新疆生产建设兵团累计报告接种新冠病毒疫苗超过33亿剂次,用科学记数法表示33亿是( )A、 B、 C、 D、3. “天宫课堂”第二课3月23日在中国空间站开讲,包括六个项目:太空“冰雪”实验、液桥演示实验、水油分离实验、太空抛物实验、空间科学设施介绍与展示、天地互动环节.若随机选取一个项目写观后感,则恰好选到“实验”项目的概率是( )A、 B、 C、 D、4. 下列算式中,正确的是( )A、 B、 C、 D、5. 超市货架上有一批大小不一的鸡蛋,某顾客从中选购了部分大小均匀的鸡蛋,设货架上原有鸡蛋的质量(单位:g)平均数和方差分别为 , s2 , 该顾客选购的鸡蛋的质量平均数和方差1 , , 则下列结论一定成立的是( )A、1 B、1 C、s2> D、s26. 实数a在数轴上的对应点的位置如图所示.若实数 满足 ,则b的值可以是( )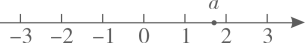 A、2 B、-1 C、-2 D、-37. 如图,△ABC的顶点A.B.C均在⊙O上,若∠ABC+∠AOC=90°,则∠AOC的大小是( )
A、2 B、-1 C、-2 D、-37. 如图,△ABC的顶点A.B.C均在⊙O上,若∠ABC+∠AOC=90°,则∠AOC的大小是( )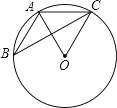 A、30° B、45° C、60° D、70°8. 如图,在平行四边形ABCD中,AB=5,BC=8,以点D为圆心,任意长为半径画弧,交AD于点P , 交CD于点Q , 分别以P、Q为圆心,大于 PQ为半径画弧交于点M , 连接DM并延长,交BC于点E , 连接AE , 恰好有AE⊥BC , 则AE的长为( )
A、30° B、45° C、60° D、70°8. 如图,在平行四边形ABCD中,AB=5,BC=8,以点D为圆心,任意长为半径画弧,交AD于点P , 交CD于点Q , 分别以P、Q为圆心,大于 PQ为半径画弧交于点M , 连接DM并延长,交BC于点E , 连接AE , 恰好有AE⊥BC , 则AE的长为( ) A、3 B、4 C、5 D、9. 已知抛物线(a,b,c均为常数,)的顶点是 , 且该抛物线经过点 , , 若 , 则的取值范围是( )A、 B、 C、 D、且10. 如图,△ABC中,∠ABC=45°,BC=4,tan∠ACB=3,AD⊥BC于D,若将△ADC绕点D逆时针方向旋转得到△FDE,当点E恰好落在AC上,连接AF.则AF的长为( )
A、3 B、4 C、5 D、9. 已知抛物线(a,b,c均为常数,)的顶点是 , 且该抛物线经过点 , , 若 , 则的取值范围是( )A、 B、 C、 D、且10. 如图,△ABC中,∠ABC=45°,BC=4,tan∠ACB=3,AD⊥BC于D,若将△ADC绕点D逆时针方向旋转得到△FDE,当点E恰好落在AC上,连接AF.则AF的长为( )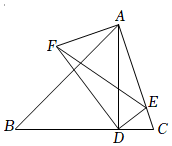 A、 B、 C、 D、2
A、 B、 C、 D、2二、填空题
-
11. 因式分解:2a2﹣8= .12. 函数y=中自变量x的取值范围是13. 一桶油漆能刷的面积,用它恰好刷完10个同样的正方体形状盒子的全部外表面.设其中一个盒子的棱长为xdm,则可列出方程: .14. 一个正多边形内接于半径为4的⊙O,AB是它的一条边,扇形OAB的面积为 , 则这个正多边形的边数是 .15. 如图,在矩形中, , , 点N是边上的中点,点M是边上的一动点连接 , 将沿折叠,若点B的对应点 , 连接 , 当为直角三角形时,的长为 .

三、解答题
-
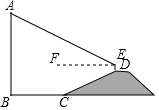
16. 计算: .17. 先化简,再求值: , 其中x=118. 如图,AB是垂直于水平面的建筑物,为测量AB的高度,小红从建筑物底端B出发,沿水平方向行走了52米到达点C,然后沿斜坡CD前进,到达坡顶D点处,DC=BC.在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角∠AEF为27°(点A,B,C,D在同一平面内),斜坡CD的坡度(或坡比)i=1:2.4,求建筑物AB的高度.(精确到个位)(参考数据:sin=27°≈0.45,cos27°≈0.89,tan27°≈0.51)
 19. 如图,在中,与分别相切于点E,F,平分 , 连接 .
19. 如图,在中,与分别相切于点E,F,平分 , 连接 . (1)、求证:是的切线;(2)、若 , 的半径是2,求图中阴影部分的面积.20. 端午节前夕,某大型超市采购了一批礼盒进行销售,这批礼盒有甲型和乙型两种共600个,其进价与标价如下表所示(单位:元):
(1)、求证:是的切线;(2)、若 , 的半径是2,求图中阴影部分的面积.20. 端午节前夕,某大型超市采购了一批礼盒进行销售,这批礼盒有甲型和乙型两种共600个,其进价与标价如下表所示(单位:元):进价
标价
甲型
90
120
乙型
50
60
(1)、该超市将甲型礼盒按标价的九折销售,乙型礼盒按标价进行销售,当销售完这批礼盒后可获利9200元,求该商场购进甲型、乙型这两种礼盒各多少个?(2)、这批礼盒销售完毕后,该超市计划再次按原进价购进甲、乙两种礼盒共200个,且均按标价进行销售,请问如何进货能保证这批礼盒销售完之后获得利润最大,且利润不能超过成本的25%.21. 在初中阶段的函数学习中,我们经历了“确定函数的表达式——利用函数图象研究其性质——运用函数解决问题”的学习过程.在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.同时,我们也学习了绝对值的意义 .结合上面经历的学习过程,现在来解决下面的问题:
在函数中,当时,;当时, .
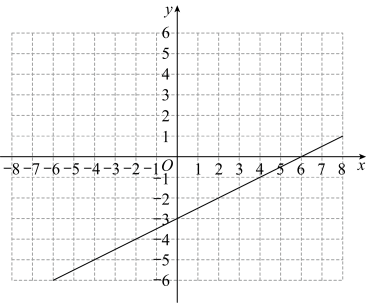 (1)、求这个函数的表达式;(2)、在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数的图象,并写出这个函数的一条性质;(3)、已知函数的图象如图所示,结合你所画的函数图象,直接写出不等式的解集.(4)、若方程有四个不相等的实数根,则实数的取值范围是 .22. 如图
(1)、求这个函数的表达式;(2)、在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数的图象,并写出这个函数的一条性质;(3)、已知函数的图象如图所示,结合你所画的函数图象,直接写出不等式的解集.(4)、若方程有四个不相等的实数根,则实数的取值范围是 .22. 如图 (1)、证明推断:如图(1),在正方形 中,点E,Q分别在边 上, 于点O,点G,F分别在边 上, .求证: ;(2)、类比探究:如图(2),在矩形 中, (k为常数).将矩形 沿 折叠,使点A落在 边上的点E处,得到四边形 交 于点H,连接 交 于点O.试探究 与 之间的数量关系,并说明理由;(3)、拓展应用:在(2)的条件下,连接 ,当时 ,若 ,求 的长.
(1)、证明推断:如图(1),在正方形 中,点E,Q分别在边 上, 于点O,点G,F分别在边 上, .求证: ;(2)、类比探究:如图(2),在矩形 中, (k为常数).将矩形 沿 折叠,使点A落在 边上的点E处,得到四边形 交 于点H,连接 交 于点O.试探究 与 之间的数量关系,并说明理由;(3)、拓展应用:在(2)的条件下,连接 ,当时 ,若 ,求 的长.