广东省深圳市光明区2023年中考一模数学试卷
试卷更新日期:2023-04-06 类型:中考模拟
一、单选题
-
1. 下列四个数中,最大的负数是( )A、 B、 C、0 D、20232. 如图的五个甲骨文中,既不是轴对称图形,也不是中心对称图形的有( )
 A、1个 B、2个 C、3个 D、4个3. 下列运算正确的是( )A、 B、 C、 D、4. 用反证法证明命题“三角形中必有一个内角小于或等于60°”时,首先应该假设这个三角形中( )A、有一个内角小于60° B、每一个内角都小于60° C、有一个内角大于60° D、每一个内角都大于60°5. 如图,AB∥CE , ∠A=40°,CE=DE , 则∠C的度数是( )
A、1个 B、2个 C、3个 D、4个3. 下列运算正确的是( )A、 B、 C、 D、4. 用反证法证明命题“三角形中必有一个内角小于或等于60°”时,首先应该假设这个三角形中( )A、有一个内角小于60° B、每一个内角都小于60° C、有一个内角大于60° D、每一个内角都大于60°5. 如图,AB∥CE , ∠A=40°,CE=DE , 则∠C的度数是( ) A、40° B、30° C、20° D、15°6. 下列说法中,正确的是( )A、当x≠-1时, 有意义 B、对角线相等的四边形是矩形 C、三角形三边垂直平分线的交点到三个顶点的距离相等 D、若a<b则一定成立7. 疫情期间居民为了减少外出时间,更愿意使用在线上买菜,某买菜今年一月份新进册用户为200万,三月份新注册用户为338万,则二、三两个月新注册用户每月平均增长率是( )A、 B、 C、 D、8. 如图,在平行四边形ABCD中,AB=5,BC=8,以点D为圆心,任意长为半径画弧,交AD于点P , 交CD于点Q , 分别以P、Q为圆心,大于 PQ为半径画弧交于点M , 连接DM并延长,交BC于点E , 连接AE , 恰好有AE⊥BC , 则AE的长为( )
A、40° B、30° C、20° D、15°6. 下列说法中,正确的是( )A、当x≠-1时, 有意义 B、对角线相等的四边形是矩形 C、三角形三边垂直平分线的交点到三个顶点的距离相等 D、若a<b则一定成立7. 疫情期间居民为了减少外出时间,更愿意使用在线上买菜,某买菜今年一月份新进册用户为200万,三月份新注册用户为338万,则二、三两个月新注册用户每月平均增长率是( )A、 B、 C、 D、8. 如图,在平行四边形ABCD中,AB=5,BC=8,以点D为圆心,任意长为半径画弧,交AD于点P , 交CD于点Q , 分别以P、Q为圆心,大于 PQ为半径画弧交于点M , 连接DM并延长,交BC于点E , 连接AE , 恰好有AE⊥BC , 则AE的长为( ) A、3 B、4 C、5 D、9. 二次函数的图像如图所示,其对称轴是直线x=1,则函数y=ax+b和y=的大致图像是( )
A、3 B、4 C、5 D、9. 二次函数的图像如图所示,其对称轴是直线x=1,则函数y=ax+b和y=的大致图像是( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,在 中,D是BC边上的中点,连接AD,把 沿AD翻折,得到 , 与AC交于点E,若 , , ,则 的面积是( )
10. 如图,在 中,D是BC边上的中点,连接AD,把 沿AD翻折,得到 , 与AC交于点E,若 , , ,则 的面积是( )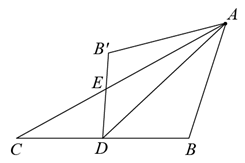 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 因式分解:2a2﹣8= .12. 在一个不透明的口袋中装有4个只有颜色不同的球,其中红球1个,白球2个,黄球1个,搅匀后随机摸出两个球,恰好都是白球的概率是13. 如图,直角 中, ,根据作图痕迹,若 , ,则 cm.
 14. 如图,点A是函数 ( )的图象上任意一点, 轴交函数 ( )的图象于点B,以AB为边作平行四边形ABCD,且 ,C、D在x轴上,则 .
14. 如图,点A是函数 ( )的图象上任意一点, 轴交函数 ( )的图象于点B,以AB为边作平行四边形ABCD,且 ,C、D在x轴上,则 . 15. 如图,在平行四边形ABCD中,E为CD中点,连接BE,F为BE中点,连接AF,若 , , .则AF长为 .
15. 如图,在平行四边形ABCD中,E为CD中点,连接BE,F为BE中点,连接AF,若 , , .则AF长为 .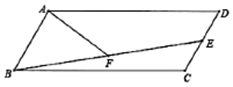
三、解答题
-
16. 计算: .17. 先化简,再求值: , 其中x=118. 深圳中小学现已开展延时服务,某校为了解学生的兴趣,现随机抽取部分学生进行问卷调查后(每人只能选一种)将调查结果绘制成如图所示的统计图:
 (1)、本次随机调查了名学生;(2)、请补全条形统计图;(3)、扇形统计图中,C类所对应的扇形的圆心角为度;(4)、若该学校共有学生2400名,则选择“D:其它”的学生大约有名.19. 如图,AB是 的直径,弦 ,E是OB的中点,连接CE并延长到点F,使 ,连接AF交 于点D,连接BD,BF.
(1)、本次随机调查了名学生;(2)、请补全条形统计图;(3)、扇形统计图中,C类所对应的扇形的圆心角为度;(4)、若该学校共有学生2400名,则选择“D:其它”的学生大约有名.19. 如图,AB是 的直径,弦 ,E是OB的中点,连接CE并延长到点F,使 ,连接AF交 于点D,连接BD,BF. (1)、求证:直线BF是 的切线;(2)、若AF长为 ,求BD的长.20. 某网络经销商购进了一批以冬奥会为主题的文化衫进行销售,文化衫的进价为每件40元,每月销售量y(件)与销售单价x(元)之间的函数关系如图所示.
(1)、求证:直线BF是 的切线;(2)、若AF长为 ,求BD的长.20. 某网络经销商购进了一批以冬奥会为主题的文化衫进行销售,文化衫的进价为每件40元,每月销售量y(件)与销售单价x(元)之间的函数关系如图所示. (1)、求出每月的销售量y(件)与销售单价x(元)之间的函数关系式;(2)、设每月获得的利润为W(元).这种文化衫销售单价定为多少元时,每月的销售利润最大?最大利润是多少元?21. 如图1,已知⊙O是△ABC的外接圆,∠ABC=∠ACB=(45°<<90°),点D是上一点,连接CD交AB于E.
(1)、求出每月的销售量y(件)与销售单价x(元)之间的函数关系式;(2)、设每月获得的利润为W(元).这种文化衫销售单价定为多少元时,每月的销售利润最大?最大利润是多少元?21. 如图1,已知⊙O是△ABC的外接圆,∠ABC=∠ACB=(45°<<90°),点D是上一点,连接CD交AB于E. (1)、连接BD,若∠CDB=40°,求的大小;(2)、如图2,若点B恰好是中点,求证:;
(1)、连接BD,若∠CDB=40°,求的大小;(2)、如图2,若点B恰好是中点,求证:; (3)、如图3,将CD分别沿BC、AC翻折到CM、CN,连接MN,若CD为直径,请问是否为定值,若是请求出这个值,若不是,请说明理由;
(3)、如图3,将CD分别沿BC、AC翻折到CM、CN,连接MN,若CD为直径,请问是否为定值,若是请求出这个值,若不是,请说明理由; 22. 综合与实践
22. 综合与实践问题情境:数学活动课上,老师出示了一个问题:如图①,在中, , 垂足为E,F为的中点,连接 , , 试猜想与的数量关系,并加以证明.


 (1)、独立思考:请解答老师提出的问题;(2)、实践探究:希望小组受此问题的启发,将沿着(F为的中点)所在直线折叠,如图②,点C的对应点为 , 连接并延长交于点G,请判断与的数量关系,并加以证明.(3)、问题解决:智慧小组突发奇想,将沿过点B的直线折叠,如图③,点A的对应点为 , 使于点H,折痕交于点M,连接 , 交于点N.该小组提出一个问题:若此的面积为20,边长 , , 求图中阴影部分(四边形)的面积.请你思考此问题,直接写出结果.
(1)、独立思考:请解答老师提出的问题;(2)、实践探究:希望小组受此问题的启发,将沿着(F为的中点)所在直线折叠,如图②,点C的对应点为 , 连接并延长交于点G,请判断与的数量关系,并加以证明.(3)、问题解决:智慧小组突发奇想,将沿过点B的直线折叠,如图③,点A的对应点为 , 使于点H,折痕交于点M,连接 , 交于点N.该小组提出一个问题:若此的面积为20,边长 , , 求图中阴影部分(四边形)的面积.请你思考此问题,直接写出结果.