广东省深圳市福田区2023年九年级3月质量检测数学试题
试卷更新日期:2023-04-06 类型:中考模拟
一、单选题
-
1. 下列四个选项中,为负整数的是( )A、0 B、 C、 D、2. 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 2022年深圳全市地区生产总值3.24万亿元.3.24万亿用科学记数法表示为( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,一个含有角的直角三角尺的两个顶点放在直尺的对边上.如果 , 那么的度数是( )
3. 2022年深圳全市地区生产总值3.24万亿元.3.24万亿用科学记数法表示为( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,一个含有角的直角三角尺的两个顶点放在直尺的对边上.如果 , 那么的度数是( ) A、 B、 C、 D、6. 一件商品售价元,利润率为 , 则这种商品每件的成本是( )元.A、 B、 C、 D、7. 如图,甲乙两楼相距30米,乙楼高度为36米,自甲楼顶A处看乙楼楼顶B处仰角为 , 则甲楼高度为( )
A、 B、 C、 D、6. 一件商品售价元,利润率为 , 则这种商品每件的成本是( )元.A、 B、 C、 D、7. 如图,甲乙两楼相距30米,乙楼高度为36米,自甲楼顶A处看乙楼楼顶B处仰角为 , 则甲楼高度为( ) A、15米 B、米 C、米 D、米8. 下列说法正确的是( )A、对角线互相垂直的四边形是菱形 B、对应边成比例的四边形是相似四边形 C、二次函数(为常数)的图象与轴有两个交点 D、若代数式在实数范围内有意义,则9. 我们定义一种新函数:形如的函数叫做“鹊桥”函数.数学兴趣小组画出一个“鹊桥”函数的图像如图所示,则下列结论正确的是( )
A、15米 B、米 C、米 D、米8. 下列说法正确的是( )A、对角线互相垂直的四边形是菱形 B、对应边成比例的四边形是相似四边形 C、二次函数(为常数)的图象与轴有两个交点 D、若代数式在实数范围内有意义,则9. 我们定义一种新函数:形如的函数叫做“鹊桥”函数.数学兴趣小组画出一个“鹊桥”函数的图像如图所示,则下列结论正确的是( ) A、 B、 C、当直线与该图像恰有三个公共点时,则 D、关于的方程的所有实数根的和为410. 如图,四边形和四边形均为正方形,点为的中点,若 , 连接 , 则的长为( )
A、 B、 C、当直线与该图像恰有三个公共点时,则 D、关于的方程的所有实数根的和为410. 如图,四边形和四边形均为正方形,点为的中点,若 , 连接 , 则的长为( )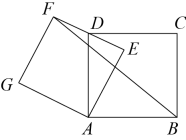 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分解因式: .12. 宝鸡“我要上全运”马拉松赛事设有A“全程马拉松”,B“半程马拉松”,C:“嘉年华马拉松”三个项目,小智和小慧参加了该赛事的志愿者服务工作,组委会将志愿者随机分配到三个项目组.小智和小慧被分到同一个项目组进行志愿服务的概率.13. 如图所示,在中, , 按以下步骤作图:①以点为圆心,以小于的长为半径作弧,分别交、于点 , ;②分别以点 , 为圆心,以大于的长为半径作弧,两弧相交于点;③作射线 , 交于点 , 若 , . 则的长为 .
 14. 如图,反比例函数的图象经过点 , 将线段沿轴向右平移至 , 反比例函数的图象经过点 . 若线段扫过的面积为 , 则的值为
14. 如图,反比例函数的图象经过点 , 将线段沿轴向右平移至 , 反比例函数的图象经过点 . 若线段扫过的面积为 , 则的值为 15. 如图,在中, , 点在边上, , 将沿折叠,的对应边交于点 , 连接 . 若 , , 则的长为
15. 如图,在中, , 点在边上, , 将沿折叠,的对应边交于点 , 连接 . 若 , , 则的长为
三、解答题
-
16. 计算:17. 先化简: ,并在 中选一个合适的数求值.18. 为了解学生的睡眠情况,某校随机抽取部分学生对他们最近两周的睡眠情况进行调查,得到他们每日平均睡眠时长x(单位:h)的一组数据,将所得数据分为四组(A:x<8;B:8≤x<9;C:9≤x<10;D:x≥10),并绘制成如下两幅不完整的统计图.
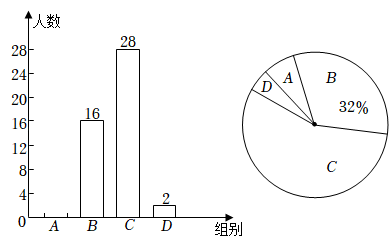
根据以上信息,解答下列问题:
(1)、本次一共抽样调查了名学生.(2)、求出扇形统计图中D组所对应的扇形圆心角的度数.(3)、将条形统计图补充完整.(4)、若该校共有1200名学生,请估计最近两周有多少名学生的每日平均睡眠时长大于或等于9h.19. 某企业计划购买A、两种型号的机器人来搬运货物,已知每台A型机器人比每台型机器人每天少搬运10吨,且A型机器人每天搬运540吨货物与型机器人每天搬运600吨货物所需台数相同.(1)、求每台A型机器人和每台型机器人每天分别搬运货物多少吨?(2)、每台A型机器人售价1.2万元,每台型机器人售价2万元,该公司计划采购A、两种型号的机器人共30台,必须满足每天搬运的货物不低于2830吨,购买金额不超过48万元.请你求出最节省的采购方案,购买总金额最低是多少万元?20. 如图,为的直径,点在直径上(点与A,两点不重合), , 点在上满足 , 连接并延长到点,使 . (1)、求证:是的切线;(2)、若 , 求的值.21. 【综合实践】
(1)、求证:是的切线;(2)、若 , 求的值.21. 【综合实践】某公园在人工湖里安装一个喷泉,在湖心处竖直安装一根水管,在水管的顶端安一个喷水头,喷出的水柱形状可以看作是抛物线的一部分.若记水柱上某一位置与水管的水平距离为米,与湖面的垂直高度为米.下面的表中记录了与的五组数据:
(米)
0
1
2
3
4
(米)
0.5
1.25
1.5
1.25
0.5
(1)、在下面网格(图1)中建立适当的平面直角坐标系,并根据表中所给数据画出表示与函数关系的图象; (2)、若水柱最高点距离湖面的高度为米,则 ▲ , 并求与函数表达式;(3)、现公园想通过喷泉设立新的游玩项目,准备通过只调节水管露出湖面的高度,使得游船能从抛物线形水柱下方通过,如图2所示,为避免游船被喷泉淋到,要求游船从抛物线形水柱下方中间通过时,顶棚上任意一点到水柱的竖直距离均不小于0.5米,已知游船顶棚宽度为3米,顶棚到湖面的高度为2米,那么公园应将水管露出湖面的高度(喷水头忽略不计)至少调节到多少米才能符合要求?请通过计算说明理由(结果保留一位小数).22.(1)、【问题初探】
(2)、若水柱最高点距离湖面的高度为米,则 ▲ , 并求与函数表达式;(3)、现公园想通过喷泉设立新的游玩项目,准备通过只调节水管露出湖面的高度,使得游船能从抛物线形水柱下方通过,如图2所示,为避免游船被喷泉淋到,要求游船从抛物线形水柱下方中间通过时,顶棚上任意一点到水柱的竖直距离均不小于0.5米,已知游船顶棚宽度为3米,顶棚到湖面的高度为2米,那么公园应将水管露出湖面的高度(喷水头忽略不计)至少调节到多少米才能符合要求?请通过计算说明理由(结果保留一位小数).22.(1)、【问题初探】如图1,等腰中, , 点为边一点,以为腰向下作等腰 , . 连接 , , 点为的中点,连接 . 猜想并证明线段与的数量关系和位置关系.
 (2)、【深入探究】
(2)、【深入探究】在(1)的条件下 , 如图2,将等腰绕点旋转,上述结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
 (3)、【拓展迁移】
(3)、【拓展迁移】如图3,等腰中, , . 在中, , . 连接 , , 点为的中点,连接 .

绕点旋转过程中,
①线段与的数量关系为:;
②若 , , 当点在等腰内部且的度数最大时,线段的长度为 .