广东省汕头市潮阳区2023年九年级下学期学年考试数学卷（镇性联考）

试卷更新日期：2023-04-06 类型：中考模拟

进入出卷网下载

一、单选题

1. 一元二次方程 $x^{2} + 2 x + 1 = 0$ 的解是（）

A、 $x_{1} = 1, x_{2} = - 1$ B、 $x_{1} = x_{2} = 1$ C、 $x_{1} = x_{2} = - 1$ D、 $x_{1} = - 1, x_{2} = 2$

查看试题解析
2. 圆锥的侧面展开图是（　　）

A、三角形 B、矩形 C、扇形 D、圆

查看试题解析
3. 在下列四个图案中，不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 已知反比例函数 $y = \frac{6}{x}$ ，则下列描述错误的是（）

A、图象位于第一，第三象限 B、图象必经过点 $(4 ， \frac{3}{2})$ C、图象不可能与坐标轴相交 D、 $y$ 随 $x$ 的增大而减小

查看试题解析
5. 在Rt△ABC中，∠C=90°，如果BC=2，sinA= $\frac{2}{3}$ ，那么AB的长是（）

A、3 B、 $\frac{4}{3}$ C、 $\sqrt{5}$ D、 $\sqrt{13}$

查看试题解析
6. 如图，将 $△ A B C$ 绕点 $A$ 逆时针旋转 $55 °$ 得到 $△ A D E$ ，若 $∠ E = 70 °$ 且 $A D ⊥ B C$ 于点 $F$ ，则 $∠ B A C$ 的度数为（）

A、 $65 °$ B、 $70 °$ C、 $75 °$ D、 $80 °$

查看试题解析
7. 如图， $⊙ O$ 的直径 $C D = 20$ ， $A B$ 是 $⊙ O$ 的弦， $A B ⊥ C D$ ，垂足为 $M$ ， $O M$ ： $O C = 3$ ：5，则 $A B$ 的长为（）

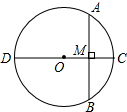A、8 B、12 C、16 D、 $2 \sqrt{91}$

查看试题解析
8. 从1、2、3、4四个数中随机选取两个不同的数，分别记为a、c ，则关于x的一元二次方程ax²＋4x＋c＝0有实数解的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
9. 如图，在△ABC中，点D在AB边上，若BC=3， BD=2，且∠BCD=∠A，则线段AD的长为（）

A、2 B、 $\frac{5}{2}$ C、3 D、 $\frac{9}{2}$

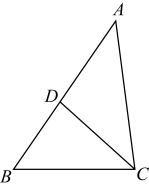查看试题解析
10. 如图，二次函数y＝ax²+bx+c（a＞0）的图象与x轴交于A，B两点，与y轴正半轴交于点C，它的对称轴为直线x＝﹣1.则下列选项中正确的是（　　）

A、abc＜0 B、4ac﹣b²＞0 C、c﹣a＞0 D、当x＝﹣n²﹣2（n为实数）时，y≥c

查看试题解析

二、填空题

11. 请写出一个函数表达式，使其图象的对称轴为 $y$ 轴：.

查看试题解析
12. 如图，A，B，C是 $⊙ O$ 上的三点，若 $Δ O B C$ 是等边三角形，则 $\cos ∠ A =$ ．

查看试题解析
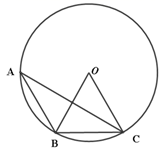13. 一个不透明布袋中有4个红球，2个白球，这些球除颜色外无其他差别，从中随机模出一个小球，该小球是红色的概率为．

查看试题解析
14. 已知x=1是一元二次方程（m-2）x²+4x-m²=0的一个根，则m的值是．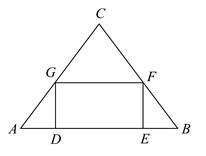

查看试题解析
15. 如图，在 $△ A B C$ 中， $A C = B C$ ，矩形 $D E F G$ 的顶点D、E在 $A B$ 上，点F、G分别在 $B C$ 、 $A C$ 上，若 $C F = 4$ ， $B F = 3$ ，且 $D E = 2 E F$ ，则 $E F$ 的长为.

查看试题解析

三、解答题

16. 计算： ${(3.14 - π)}^{0} - 9 t a n 30 ° + | 1 - \sqrt{3} | + 4 s i n 60 °$ ．

查看试题解析
17. 有一人感染了某种病毒，经过两轮传染后，共有256人感染了该种病毒，求每轮传染中平均每人传染了多少个人．

查看试题解析
18. 如图，在边长为1的正方形网格中建立平面直角坐标系，已知 $△ A B C$ 三个顶点分别为 $A (- 1 ， 2) 、 B (2 ， 1) 、 C (4 ， 5)$ ．

(1)、以原点O为位似中心，在x轴的上方画出 $△ A_{1} B_{1} C_{1}$ ，使 $△ A_{1} B_{1} C_{1}$ 与 $△ A B C$ 位似，且相似比为 $2 ： 1$ ；

(2)、 $△ A_{1} B_{1} C_{1}$ 的面积为．

查看试题解析
19. 今年某市为创评“全国文明城市”称号，周末团市委组织志愿者进行宣传活动.班主任梁老师决定从4名女班干部（小悦、小惠、小艳和小倩）中通过抽签的方式确定2名女生去参加.
抽签规则：将4名女班干部姓名分别写在4张完全相同的卡片正面，把四张卡片背面朝上，洗匀后放在桌面上，梁老师先从中随机抽取一张卡片，记下姓名，再从剩余的3张卡片中随机抽取第二张，记下姓名.

(1)、该班男生“小刚被抽中”是事件，“小悦被抽中”是事件(填“不可能”或“必然”或“随机”)；第一次抽取卡片“小悦被抽中”的概率为；

(2)、试用画树状图或列表的方法表示这次抽签所有可能的结果，并求出“小惠被抽中”的概率.

查看试题解析
20.
如图，在平面直角坐标系中，点A（ $\sqrt{3}$ ， 1）、B（2，0）、O（0，0），反比例函数y= $\frac{k}{x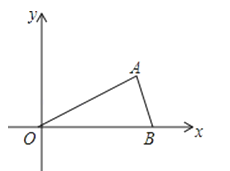}$ 图象经过点A．

(1)、求k的值

(2)、将△AOB绕点O逆时针旋转60°，得到△COD，其中点A与点C对应，试判断点D是否在该反比例函数的图象上？

查看试题解析
21. 已知：如图，在菱形ABCD中，点E、F分别在边AB、AD上，BE=DF，CE的延长线交DA的延长线于点G，CF的延长线交BA的延长线于点H．

(1)、求证：△BEC∽△BCH；

(2)、如果BE²=AB·AE，求证：AG=DF．

查看试题解析
22. 在平面直角坐标系中，已知点 $A (1 ， 2) ， B (2 ， 3) ， C (2 ， 1)$ ，直线 $y = x + m$ 经过点A，抛物线 $y = a x^{2} + b x + 1$ 恰好经过A，B，C三点中的两点．

(1)、求直线 $y = x + m$ 的解析式；

(2)、求a，b的值；

(3)、平移抛物线 $y = a x^{2} + b x + 1$ ，使其顶点仍在直线 $y = x + m$ 上，求平移后所得抛物线与y轴交点纵坐标的最大值．

查看试题解析
23. 如图， $P A$ 、 $P B$ 是 $⊙ O$ 的切线， $A$ 、 $B$ 是切点， $A C$ 是 $⊙ O$ 的直径，连接 $O P$ ，交 $⊙ O$ 于点 $D$ ，交 $A B$ 于点 $E$ ．

(1)、求证： $B C ∥ O P$ ；

(2)、若 $E$ 恰好是 $O D$ 的中点，且四边形 $O A P B$ 的面积是 $16 \sqrt{3}$ ，求阴影部分的面积；

(3)、若 $s i n ∠ B A C = \frac{1}{3}$ ，且 $A D = 2 \sqrt{3}$ ，求切线 $P A$ 的长．

查看试题解析