广东省茂名市茂南区2023年九年级中考一模质量检测数学试题

试卷更新日期：2023-04-06 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数中，负数是（）

A、 $- 1$ B、0 C、2 D、 $\sqrt{2}$

查看试题解析
2. 预计到2025年我国高铁运营里程将达到385000千米，将数据385000用科学记数法表示为（）

A、3.85×10⁶ B、3.85×10⁵ C、38.5×10⁵ D、0.385×10⁶

查看试题解析
3. 下列图形中，是中心对称图形但不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 将抛物线 $y = - 3 (x + 1)^{2} + 3$ 向右平移 $2$ 个单位，再向下平移 $1$ 个单位，得到抛物线的解析式为（）

A、 $y = - 3 (x + 3)^{2} + 4$ B、 $y = - 3 (x - 1)^{2} + 2$ C、 $y = - 3 (x + 3)^{2} + 2$ D、 $y = - 3 (x - 1)^{2} + 4$

查看试题解析
5. 在Rt△ABC中，∠C=90°，BC=5，AC=12，则sinB的值是（）

A、 $\frac{5}{12}$ B、 $\frac{12}{5}$ C、 $\frac{5}{13}$ D、 $\frac{12}{13}$

查看试题解析
6. 已知 $\sqrt{a - 2} + | b - 2 a | = 0$ ，则a+2b的值是（）

A、4 B、6 C、8 D、10

查看试题解析
7. 关于 $x$ 的一元二次方程 $x^{2} - 3 x + m = 0$ 有实数根，则实数m的取值范围是（）

A、 $m < \frac{9}{4}$ B、 $m \leq \frac{9}{4}$ C、 $m > \frac{9}{4}$ D、 $m \geq \frac{9}{4}$

查看试题解析
8. 如图，在Rt△ABC中，∠B＝90°，分别以A，C为圆心，大于 $\frac{1}{2}$ AC长为半径画弧，两弧相交于点M，N，作直线MN，与AC，BC分别交于点D，点E，连结AE，当AB＝5，BC＝9时，则△ABE的周长是（）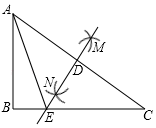

A、19 B、14 C、4 D、13

查看试题解析
9. 如图，PA、PB是⊙O的切线，切点分别为A、B ，若OA＝2，∠P＝60°，则 $\overset{⌢}{A B}$ 的长为（）

A、 $\frac{2}{3}$ π B、π C、 $\frac{4}{3} π$ D、 $\frac{5}{3} π$

查看试题解析
10. 如图，正方形 $A B C D$ 中，点 $E$ 是 $A D$ 边的中点， $B D$ ， $C E$ 交于点 $H$ ， $B E$ 、 $A H$ 交于点 $G$ ，则下列结论：① $∠ A B E = ∠ D C E$ ；② $∠ A H B = ∠ E H D$ ；③ $S_{△ B H E} = S_{△ C H D}$ ；④ $A G ⊥ B E$ ．其中正确的是（）

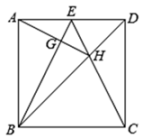A、①③ B、①②③④ C、①②③ D、①③④

查看试题解析

二、填空题

11. 计算： $3^{- 1} + \sqrt{\frac{1}{9}} + {(3 - \sqrt{3})}^{0} =$ ．

查看试题解析
12. 正多边形的一个内角是120°，则它的边数是．

查看试题解析
13. 某公司组织内部抽奖活动，共准备了 $100$ 张奖券，设一等奖 $10$ 个，二等奖 $20$ 个，三等奖 $30$ 个．若每张奖券获奖的可能性相同，则随机抽一张奖券中一等奖的概率为．

查看试题解析
14. 如果m﹣n＝3，那么2m﹣2n﹣3的值是.

查看试题解析
15. 如图，在第1个△A₁BC中，∠B＝20°，A₁B＝CB；在边A₁B上任取一点D，延长CA₁到A₂ ，使A₁A₂＝A₁D，得到第2个△A₁A₂D；在边A₂D上任取一点E，延长A₁A₂到A₃ ，使A₂A₃＝A₂E，得到第3个△A₂A₃E，…，按此方法继续下去，第2021个等腰三角形的底角度数是．

查看试题解析

三、解答题

16. 解不等式组： ${\begin{array}{l} 3 x > - 8 - x ① \\ 2 (x - 1) \leq 6 ② \end{array}$

查看试题解析
17. 如图，在 $△ A B C$ 和 $△ D C B$ 中， $B A ⊥ C A$ 于A， $C D ⊥ B D$ 于D， $A C = B D$ ， $A C$ 与 $B D$ 相交于点O．求证： $△ A B C ≌ △ D C B$ ．

查看试题解析
18. 先化简，再求值：（1- $\frac{3}{x + 2}$ ）÷ $\frac{x^{2} - 2 x + 1}{3 x + 6}$ ，其中x＝ $\sqrt{3}$ +1．

查看试题解析
19. 学校准备购置一批教师办公桌椅，已知2套A型桌椅和1套B型桌椅共需2 000元，1套A型桌椅和3套B型桌椅共需3000元．

(1)、一套A型桌椅和一套B型桌椅的售价各是多少元？

(2)、学校准备购进这两种型号的办公桌椅200套，平均每套桌椅需要运费10元，并且A型桌椅的套数不多于B型桌椅的套数的3倍．请设计出最省钱的购买方案，并说明理由．

查看试题解析
20. 某学校为了解学生上学的交通方式，现从全校学生中随机抽取了部分学生进行“我上学的交通方式”问卷调查，规定每人必须并且只能在“乘车”、“步行”、“骑车”和“其他”四项中选择一项，并将统计结果绘制了如下两幅不完整的统计图．

请解答下列问题：

(1)、在这次调查中，该学校一共抽样调查了名学生；

(2)、补全条形统计图；

(3)、若该学校共有1500名学生，试估计该学校学生中选择“步行”方式的人数．

查看试题解析
21. 如图，在Rt△ABC中，∠BAC＝90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F ．

(1)、求证：四边形ADCF是菱形；

(2)、若AC＝12，AB＝16，求菱形ADCF的面积．

查看试题解析
22. 如图，AB为⊙O的直径，C、D为⊙O上不同于A、B的两点，∠ABD＝2∠BAC，连接CD，过点C作CE⊥DB，垂足为E，直径AB与CE的延长线相交于F点.

(1)、求证：CF是⊙O的切线；

(2)、当BD＝ $\frac{18}{5}$ ，sinF＝ $\frac{3}{5}$ 时，求OF的长.

查看试题解析
23. 如图，直线 $y = k x + 2$ 与x轴交于点 $A (3 ， 0)$ ，与 $y$ 轴交于点 $B$ ，抛物线 $y = - \frac{4}{3} x^{2} + b x + 2$ 经过点 $A ， B$ ．

(1)、求 $k$ 的值和抛物线的解析式．

(2)、 $M (m ， 0)$ 为 $x$ 轴上一动点，过点 $M$ 且垂直于 $x$ 轴的直线与直线 $A B$ 及抛物线分别交于点 $P ， N$ ．若以 $O ， B ， N ， P$ 为顶点的四边形是平行四边形，求 $m$ 的值．

查看试题解析