广东省惠州市惠城区2023年九年级下学期联考数学试卷(3月)
试卷更新日期:2023-04-06 类型:中考模拟
一、单选题
-
1. −2023的绝对值是( )A、−2023 B、2023 C、±2023 D、2. 第届亚运会将于年月日至月日在中国浙江省杭州市举行,杭州奥体博览城核心区建筑总面积平方米,将数用科学记数法表示为( )A、 B、 C、 D、3. 如图,由4个相同正方体组合而成的几何体,它的左视图是( )
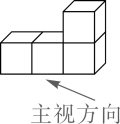 A、
A、 B、
B、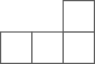 C、
C、 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )A、
4. 下列运算正确的是( )A、 B、 C、 D、5. 下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )A、 赵爽弦图
B、
赵爽弦图
B、 笛卡尔心形线
C、
笛卡尔心形线
C、 科克曲线
D、
科克曲线
D、 斐波那契螺旋线
6. 数据3,4,6,6,5的中位数是( )A、4.5 B、5 C、5.5 D、67. 已知与△相似,且相似比为 , 则与△的面积比为A、1:1 B、1:3 C、1:6 D、1:98. 抛物线的顶点坐标是( )A、 B、 C、 D、9. 已知m,n是一元二次方程x2+2x-2022=0的两个实数根,则代数式m2+4m+2n的值等于( )A、2024 B、2022 C、2020 D、201810. 如图,在正方形ABCD中,E是BC的中点,F是CD上一点, , 有下列结论:①;②;③;④ . 正确结论的个数是( )
斐波那契螺旋线
6. 数据3,4,6,6,5的中位数是( )A、4.5 B、5 C、5.5 D、67. 已知与△相似,且相似比为 , 则与△的面积比为A、1:1 B、1:3 C、1:6 D、1:98. 抛物线的顶点坐标是( )A、 B、 C、 D、9. 已知m,n是一元二次方程x2+2x-2022=0的两个实数根,则代数式m2+4m+2n的值等于( )A、2024 B、2022 C、2020 D、201810. 如图,在正方形ABCD中,E是BC的中点,F是CD上一点, , 有下列结论:①;②;③;④ . 正确结论的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 计算: =.12. 七边形的内角和是13. 如图,将三角板的直角顶点放在直尺的一边上.若 , 则的度数为 .
 14. 如图在边长相同的小正方形组成的网格中,点A、B、O在小正方形的顶点上,则 .
14. 如图在边长相同的小正方形组成的网格中,点A、B、O在小正方形的顶点上,则 .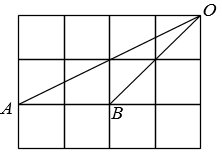 15. 如图所示的曲边三角形可按下述方法作出:作等边三角形ABC;分别以点A,B,C为圆心,以AB的长为半径作弧BC,AC,AB.三段弧所围成的图形就是一个曲边三角形,如果一个曲边三角形的周长为2π,那么这个曲边三角形的面积是.
15. 如图所示的曲边三角形可按下述方法作出:作等边三角形ABC;分别以点A,B,C为圆心,以AB的长为半径作弧BC,AC,AB.三段弧所围成的图形就是一个曲边三角形,如果一个曲边三角形的周长为2π,那么这个曲边三角形的面积是.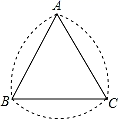
三、解答题
-
16. 已知 .(1)、化简A;(2)、若x是4的相反数,求A的值.17. 如图,矩形中, , , .
 (1)、求证:四边形是平行四边形;(2)、若四边形是菱形,求出菱形的边长.18. 某校为了开展“阳光体育运动”,计划购买篮球、足球共60个,已知每个篮球的价格为70元,每个足球的价格为80元.(1)、若购买这两类球的总金额为4600元,求篮球、足球各买了多少个?(2)、若购买篮球的总金额不超过购买足球的总金额,求最多可购买多少个篮球?19. 如图,在中, .
(1)、求证:四边形是平行四边形;(2)、若四边形是菱形,求出菱形的边长.18. 某校为了开展“阳光体育运动”,计划购买篮球、足球共60个,已知每个篮球的价格为70元,每个足球的价格为80元.(1)、若购买这两类球的总金额为4600元,求篮球、足球各买了多少个?(2)、若购买篮球的总金额不超过购买足球的总金额,求最多可购买多少个篮球?19. 如图,在中, . (1)、请用尺规作图法,在内求作 , 使 , 交于D.(不要求写作法,保留作图痕迹)(2)、在(1)的条件下,若 , , 求的长.20. “2022卡塔尔世界杯”已正式拉开战幕,足球运动备受人们的关注,某中学对部分学生就足球运动的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅统计图.根据图中信息回答下列问题:
(1)、请用尺规作图法,在内求作 , 使 , 交于D.(不要求写作法,保留作图痕迹)(2)、在(1)的条件下,若 , , 求的长.20. “2022卡塔尔世界杯”已正式拉开战幕,足球运动备受人们的关注,某中学对部分学生就足球运动的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅统计图.根据图中信息回答下列问题: (1)、接受问卷调查的学生共有人,条形统计图中m的值为;(2)、若该中学共有学生1500人,根据上述调查结果,可以估计出该学校学生中对足球知识达到“非常了解”和“基本了解”程度的总人数为人;(3)、若从足球运动达到“非常了解”程度的2名男生和2名女生中随机抽取2人解说一场足球赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.21. 设函数 , 函数( , , b是常数, , ).若函数和函数的图象交于点 , 点 ,(1)、求函数 , 的表达式;(2)、当时,比较与的大小(直接写出结果).22. 如图,四边形内接于 , 是的直径, , 垂足为E,平分 .
(1)、接受问卷调查的学生共有人,条形统计图中m的值为;(2)、若该中学共有学生1500人,根据上述调查结果,可以估计出该学校学生中对足球知识达到“非常了解”和“基本了解”程度的总人数为人;(3)、若从足球运动达到“非常了解”程度的2名男生和2名女生中随机抽取2人解说一场足球赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.21. 设函数 , 函数( , , b是常数, , ).若函数和函数的图象交于点 , 点 ,(1)、求函数 , 的表达式;(2)、当时,比较与的大小(直接写出结果).22. 如图,四边形内接于 , 是的直径, , 垂足为E,平分 .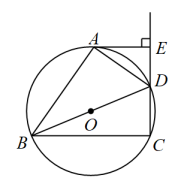 (1)、求证:是的切线;(2)、若 , , 求和弧的长.23. 如图,在平面直角坐标系中,二次函数y=-x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(-3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
(1)、求证:是的切线;(2)、若 , , 求和弧的长.23. 如图,在平面直角坐标系中,二次函数y=-x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(-3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ. (1)、求二次函数的解析式;(2)、在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;(3)、点M在抛物线上,且△AOM的面积与△AOC的面积相等,求出点M的坐标.
(1)、求二次函数的解析式;(2)、在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;(3)、点M在抛物线上,且△AOM的面积与△AOC的面积相等,求出点M的坐标.