广东省佛山市三水区2023年九年级五校联考数学中考模拟试卷
试卷更新日期:2023-04-06 类型:中考模拟
一、单选题
-
1. 下列实数: , , , , 其中最大的实数是( )A、 B、 C、 D、2. 如图是运动会领奖台,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 网络用语“6”是比较厉害的意思,且“6”本身是一个自然数,将数字用科学记数法表示( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 如果4是方程的一个根,则方程的另一个根是( )A、2 B、3 C、4 D、56. 九(1)班学生为本班一位患重病同学捐款,捐款情况如下表:
3. 网络用语“6”是比较厉害的意思,且“6”本身是一个自然数,将数字用科学记数法表示( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 如果4是方程的一个根,则方程的另一个根是( )A、2 B、3 C、4 D、56. 九(1)班学生为本班一位患重病同学捐款,捐款情况如下表:捐款金额(元)
5
10
20
50
人数(人)
9
14
11
16
则学生捐款金额的中位数是( )
A、11元 B、14元 C、10元 D、20元7. 如图,在中,延长至点 , 使 , 连接交于点 , 则的值是( ) A、 B、 C、 D、8. 不等式组的所有整数解的和为9,则整数的值有( )A、1个 B、2个 C、3个 D、4个9. 如图,菱形的边长为 , , 点 , 在菱形的边上,从点同时出发,分别沿和的方向以每秒的速度运动,到达点时停止,线段扫过区域的面积记为 , 运动时间记为 , 能大致反映y与x之间函数关系的图象是( )
A、 B、 C、 D、8. 不等式组的所有整数解的和为9,则整数的值有( )A、1个 B、2个 C、3个 D、4个9. 如图,菱形的边长为 , , 点 , 在菱形的边上,从点同时出发,分别沿和的方向以每秒的速度运动,到达点时停止,线段扫过区域的面积记为 , 运动时间记为 , 能大致反映y与x之间函数关系的图象是( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,在矩形中, , , 点为的中点,将沿折叠,使点落在矩形内点处,连接 , 则的长为( )
10. 如图,在矩形中, , , 点为的中点,将沿折叠,使点落在矩形内点处,连接 , 则的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 因式分解: .12. 如图,是一个正方体的展开图,那么写有“青”字面的对面上的字是 .
 13. 如图,中, , 以点B为圆心,的长为半径画弧交于点C,E,再分别以点C与点E为圆心,大于长的一半为半径画弧,两弧交于点F,连接交AC于点D,若 , 则是°.
13. 如图,中, , 以点B为圆心,的长为半径画弧交于点C,E,再分别以点C与点E为圆心,大于长的一半为半径画弧,两弧交于点F,连接交AC于点D,若 , 则是°.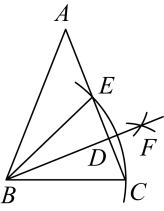 14. 如图,曲线和是两个半圆, , 大半圆半径为4,则阴影部分的面积是 .
14. 如图,曲线和是两个半圆, , 大半圆半径为4,则阴影部分的面积是 . 15. 已知二次函数的图象如图所示,有5个结论:①;②;③; ④; ⑤ , 其中正确的有是 .
15. 已知二次函数的图象如图所示,有5个结论:①;②;③; ④; ⑤ , 其中正确的有是 .
三、解答题
-
16.(1)、计算:;(2)、解分式方程: .17. 如图,在中,点D是上一点,且 , , 连接交于点F.
 (1)、若 , 求的度数;(2)、若平分 , 求证: .18. 为按照国家体育器材设施配备目录及标准要求配足体育设施器材,某校计划购买一批篮球、排球和足球,排球和足球个数相同,单价也相同.已知购买2个篮球和3个排球共需440元,购买4个篮球和5个足球共需800元.(1)、求每个篮球、排球和足球的售价;(2)、如果学校计划购买这三种球共100个,排球、足球总数不超过篮球个数的4倍,请你给出一种费用最少的购买方案,并求出该方案所需费用.19. 为落实中小学课后服务工作的要求,某校开设了四门校本课程供学生选择:A(合唱社团)、B(陶艺社团)、C(数独社团)、D(硬笔书法),七年级共有120名学生选择了C课程.为了解选择C课程学生的学习情况,张老师从这120名学生中随机抽取了30名学生进行测试,将他们的成绩(百分制,单位:分)分成六组,绘制成频数分布直方图.
(1)、若 , 求的度数;(2)、若平分 , 求证: .18. 为按照国家体育器材设施配备目录及标准要求配足体育设施器材,某校计划购买一批篮球、排球和足球,排球和足球个数相同,单价也相同.已知购买2个篮球和3个排球共需440元,购买4个篮球和5个足球共需800元.(1)、求每个篮球、排球和足球的售价;(2)、如果学校计划购买这三种球共100个,排球、足球总数不超过篮球个数的4倍,请你给出一种费用最少的购买方案,并求出该方案所需费用.19. 为落实中小学课后服务工作的要求,某校开设了四门校本课程供学生选择:A(合唱社团)、B(陶艺社团)、C(数独社团)、D(硬笔书法),七年级共有120名学生选择了C课程.为了解选择C课程学生的学习情况,张老师从这120名学生中随机抽取了30名学生进行测试,将他们的成绩(百分制,单位:分)分成六组,绘制成频数分布直方图.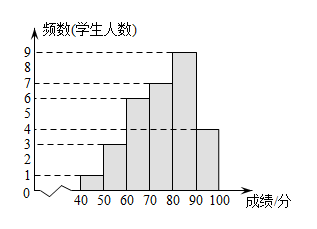 (1)、分这组的数据为:81、89、84、84、84、86、85、88、83,则这组数据的中位数是分、众数是分;(2)、根据题中信息,可以估算七年级选择C课程的学生成绩在分的人数是人;(3)、七年级每名学生必须选两门不同的课程,小明和小华在选课程的过程中,第一门都选了课程C.他俩决定随机选择第二门课程,请用列表法或树状图的方法求他俩同时选到课程A或课程B的概率.20. 如图,西安某中学依山而建,校门处有一坡度的斜坡 , 长度为米,在坡顶处看教学楼的楼顶的仰角 , 离点米远的处有一个花台,在处仰望的仰角是 , 的延长线交校门处的水平面于点 , 求楼顶的高度 . (结果保留根号)
(1)、分这组的数据为:81、89、84、84、84、86、85、88、83,则这组数据的中位数是分、众数是分;(2)、根据题中信息,可以估算七年级选择C课程的学生成绩在分的人数是人;(3)、七年级每名学生必须选两门不同的课程,小明和小华在选课程的过程中,第一门都选了课程C.他俩决定随机选择第二门课程,请用列表法或树状图的方法求他俩同时选到课程A或课程B的概率.20. 如图,西安某中学依山而建,校门处有一坡度的斜坡 , 长度为米,在坡顶处看教学楼的楼顶的仰角 , 离点米远的处有一个花台,在处仰望的仰角是 , 的延长线交校门处的水平面于点 , 求楼顶的高度 . (结果保留根号) 21. 如图,一次函数与反比例函数()的图像交于点 , , 轴于点 , 轴于点 .
21. 如图,一次函数与反比例函数()的图像交于点 , , 轴于点 , 轴于点 .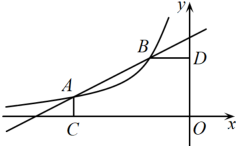 (1)、填空: , , ;(2)、观察图像,直接写出在第二象限内,反比例函数的值大于一次函数的值时的取值范围;(3)、点在线段上,连接 , , 若 , 求点的坐标.
(1)、填空: , , ;(2)、观察图像,直接写出在第二象限内,反比例函数的值大于一次函数的值时的取值范围;(3)、点在线段上,连接 , , 若 , 求点的坐标.

