安徽省蚌埠市2023年五校联考九年级下学期第一次调研数学试卷

试卷更新日期：2023-04-06 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算 $2 s i n 30 ° =$ （）

A、 $1$ B、 $\sqrt{3}$ C、 $2$ D、 $2 \sqrt{3}$

查看试题解析
2. 二次函数 $y = a {(x + 3)}^{2} - 1$ 图象的顶点坐标是（）

A、 $(3 ， 1)$ B、 $(3 ， - 1)$ C、 $(- 3 ， 1)$ D、 $(- 3 ， - 1)$

查看试题解析
3. 如图，是从上面看一个几何体得到的图形，则该几何体可能是（）

A、 B、 C、 D、

查看试题解析
4. 如图，线段AB两个端点的坐标分别为A（6，6），B（8，2），以原点O为位似中心，在第一象限内将线段AB缩小为原来的 $\frac{1}{2}$ 后得到线段CD，则端点C的坐标为（）

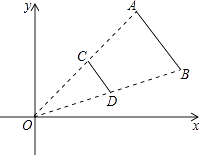A、（3，3） B、（4，3） C、（3，1） D、（4，1）

查看试题解析
5. 如图，在正六边形转盘中，有两个正三角形涂有阴影， $O A$ 为可绕点O自由转动的指针，转动指针（若指针恰好停在分界线上，则重新转动），指针落在有阴影的区域内的概率为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

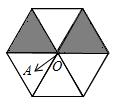查看试题解析
6. 关于x的二次函数 $y = - k x^{2} - k^{2}$ 与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 在同一平面直角坐标系内的大致图象可能是（）

A、 B、 C、 D、

查看试题解析
7. 主持人在舞台上主持节目时，站在黄金分割点上，观众看上去感觉最好．若舞台长20米，主持人从舞台一侧进入，设他至少走x米时恰好站在舞台的黄金分割点上（BP长为x），则x满足的方程是（）

A、 ${(20 - x)}^{2} = 20 x$ B、 $x^{2} = 20 (20 - x)$ C、 $x (20 - x) = 2 0^{2}$ D、以上都不对

查看试题解析
8. “如果二次函数 $y = a x^{2} + b x + c$ 的图象与x轴有两个公共点，那么一元二次方程 $a x^{2} + b x + c = 0$ 有两个不相等的实数根．”请根据你对这句话的理解，解决下面问题：若m、 $n (m < n)$ 是关于x的方程 $1 - (x - a) (x - b) = 0$ 的两根，且 $0 < a < b$ ，则a、b、m、n的大小关系是（）

A、 $m < a < b < n$ B、 $a < m < n < b$ C、 $a < m < b < n$ D、 $m < a < n < b$

查看试题解析
9. 如图，在⊙O中，直径AB＝10，弦DE⊥AB于点C，若OC：OB＝3：5，连接DO，则DE的长为（）

A、3 B、4 C、6 D、8

查看试题解析
10. 如图，在平面直角坐标系中，抛物线y＝-x²＋2 $\sqrt{3}$ x的顶点为A点，且与x轴的正半轴交于点B，P点为该抛物线对称轴上一点，则OP＋ $\frac{1}{2}$ AP的最小值为（）．

A、 $\frac{3 + 2 \sqrt{21}}{4}$ B、 $\frac{3 + 2 \sqrt{3}}{2}$ C、3 D、2 $\sqrt{3}$

查看试题解析

二、填空题

11. 如图，在 $△ A B C$ 中，D是AB中点， $D E ∥ B C$ ，若 $△ A D E$ 的面积为6，则 $△ A B C$ 的面积为．

查看试题解析
12. 如图，在 $4 \times 4$ 的方格纸中（共有16个小方格），每个小方格都是边长为1的正方形． $O$ 、A、 $B$ 分别是小正方形的顶点，则扇形 $O A B$ 的弧长等于．（结果保留根号及 $π$ ）．

查看试题解析
13. 如图，点A是函数 $y = \frac{k}{x} (x < 0)$ 的图像上的一点，过点A作 $A B ⊥ y$ 轴，垂足为点B，点C为x轴上的一点，连接AC，BC，若△ABC的面积为4，则K的值为

查看试题解析
14. 已知抛物线 $y = a x^{2} + b x - a$ ，其中 $a$ 为实数．

(1)、若抛物线经过点 $(1 ， 4)$ ，则 $b =$ ；

(2)、该抛物线经过点 $A (2 ， - a)$ ，已知点 $B (1 ， - a)$ ， $C (2 ， 2)$ ，若抛物线与线段 $B C$ 有交点，则 $a$ 的取值范围为．

查看试题解析

三、解答题

15. 计算：sin45°·cos45°-tan60°÷cos30°

查看试题解析
16. 在如图所示的正方形网格中， $△ A B C$ 的顶点均在网格上，请在所给的平面直角坐标系中按要求作图并完成填空：

(1)、作出 $△ A B C$ 向下平移5个单位的 $△ A_{1} B_{1} C_{1}$ ，写出点 $B_{1}$ 的坐标：；

(2)、作出 $△ A_{1} B_{1} C_{1}$ 绕点O逆时针旋转 $90 °$ 的 $△ A_{2} B_{2} C_{2}$ ，写出点 $A_{2}$ 的坐标．

查看试题解析
17. 为了解学生“最喜欢的课外读物类型”，学校对部分学生进行调查，并把调查信息进行整理，绘制成以下两幅不完整的统计图：（每个学生只选一种类型）其中A表示文学类，B表示科普类，C表示动漫类，D表示其他．请你根据统计图提供的信息，解答以下问题：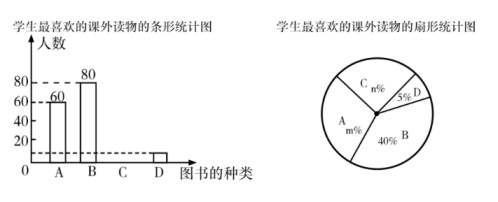

(1)、该校抽样调查的学生人数为人， $m =$ ， $n =$ ．

(2)、请补全条形统计图．

(3)、小红同学喜欢文学类图书，小明喜欢科普类图书，小华喜欢动漫类图书，学校决定从这三位同学中随机抽取两名同学到校图书馆做“图书管理员”，抽中小红的概率是多少？

查看试题解析
18. 为了测量白塔的高度AB，在D处用高为1.5米的测角仪 CD，测得塔顶A的仰角为42°，再向白塔方向前进12米，又测得白塔的顶端A的仰角为61°，求白塔的高度AB．（参考数据sin42°≈0.67，tan42°≈0.90，sin61°≈0.87，tan61°≈1.80，结果保留整数）

查看试题解析
19. 如图，四边形ABCD内接于⊙O，对角线AC与BD相交于点E，直线AM与⊙O相切于点A，交CB延长线于M，弦 $B D ∥ A M$ ．

(1)、求证：∠MAB＝∠ACD；

(2)、若AB＝5，BD＝8，求⊙O的半径．

查看试题解析
20. 如图，反比例函数 $y = \frac{k_{1}}{x}$ 的图象与正比例函数 $y = k_{2} x$ 的图象交于 $A (a ， 1)$ 、B两点．点 $M (a - 3 ， a)$ 在反比例函数图象上，连接 $O M$ ， $B M$ 交y轴于点N．

(1)、求反比例函数的解析式．

(2)、求 $△ B O M$ 的面积．

查看试题解析
21. 已知：如图，在Rt△ABC中，∠ACB＝90°，CH⊥AB，垂足为点H．点D在边BC上，联结AD，交CH于点E，且CE＝CD．

(1)、求证：△ACE∽△ABD；

(2)、求证：△ACD的面积是△ACE的面积与△ABD的面积的比例中项．

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，抛物线y=x2-4x+3与x轴交于点A 、B（点A在点B的左侧），与y轴交于点C．

(1)、求直线BC的表达式；

(2)、垂直于y轴的直线l与抛物线交于点 $P (x_{1} ， y_{1}) ， Q (x_{2} ， y_{2})$ ，与直线BC交于点 $N (x_{3} ， y_{3})$ ，若x1<x2<x3，结合函数的图象，求x1+x2+x3的取值范围.

查看试题解析
23. 如图1，在平行四边形 $A B C D$ 中， $E$ 为 $A B$ 的中点，点 $F$ 在 $A D$ 边上， $D E$ 与 $C F$ 交于点 $G$ ．

(1)、若 $G$ 为 $D E$ 的中点．
①求 $\frac{F G}{C G}$ 的值；
②连接 $E F$ ，若 $∠ E F C = 90 °$ ，求证： $D C = D F$ ．

(2)、如图2，若 $∠ E G C = ∠ A$ ，求证： $A D \cdot F C = 2 A E \cdot D E$ ．

查看试题解析