安徽省蚌埠市2023年九年级中考数学模拟试卷
试卷更新日期:2023-04-06 类型:中考模拟
一、单选题
-
1. 下列各数为负数的是( )A、 B、 C、 D、2. 近年来,我国能源保供稳价政策有力推进,能源先进产能平稳有序释放,规模以上工业原煤、原油、天然气和电力生产同比保持增长.其中2022年1—11月份,我国生产原煤40.9亿吨.40.9亿用科学记数法表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 图中所示的几何体为圆台,其主(正)视图正确的是( )
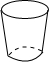 A、
A、 B、
B、 C、
C、 D、
D、 5. 如图所示, , , 点B,O,D在同一直线上,则的度数为( )
5. 如图所示, , , 点B,O,D在同一直线上,则的度数为( ) A、 B、 C、 D、6. 如图,AB是⊙O直径,弦CD⊥AB于点E.若CD=6,OE=4,则⊙O的直径为( )
A、 B、 C、 D、6. 如图,AB是⊙O直径,弦CD⊥AB于点E.若CD=6,OE=4,则⊙O的直径为( )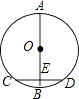 A、5 B、6 C、8 D、107. 在一条笔直的公路上A、B两地相120km,甲车从A地开往B地,乙车从B地开往A地,甲比乙先出发.设甲、乙两车距A地的路程为y千米,甲车行驶的时间为x小时,y与x之间的关系如图所示,下列说法错误的是( )
A、5 B、6 C、8 D、107. 在一条笔直的公路上A、B两地相120km,甲车从A地开往B地,乙车从B地开往A地,甲比乙先出发.设甲、乙两车距A地的路程为y千米,甲车行驶的时间为x小时,y与x之间的关系如图所示,下列说法错误的是( ) A、甲车的速度比乙的速度慢 B、甲车出发1小时后乙才出发 C、甲车行驶了2.8h或3.2h时,甲、乙两车相距10km D、乙车达到A地时,甲车离A地90km8. 在一个不透明的口袋中,放置6个黄球、1个红球和n个蓝球,这些小球除颜色外其余均相同,课外兴趣小组每次摸出一个球记录下颜色后再放回,并且统计了黄球出现的频率,如图,则n的值是( )
A、甲车的速度比乙的速度慢 B、甲车出发1小时后乙才出发 C、甲车行驶了2.8h或3.2h时,甲、乙两车相距10km D、乙车达到A地时,甲车离A地90km8. 在一个不透明的口袋中,放置6个黄球、1个红球和n个蓝球,这些小球除颜色外其余均相同,课外兴趣小组每次摸出一个球记录下颜色后再放回,并且统计了黄球出现的频率,如图,则n的值是( ) A、2 B、3 C、5 D、89. 二次函数的图象如图所示,则一次函数与反比例函数在同一坐标系内的大致图象是( )
A、2 B、3 C、5 D、89. 二次函数的图象如图所示,则一次函数与反比例函数在同一坐标系内的大致图象是( )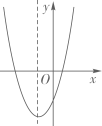 A、
A、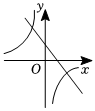 B、
B、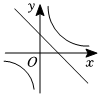 C、
C、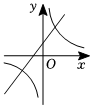 D、
D、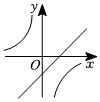 10. 如图,在正方形中, , E是的中点,F是延长线上的点,将沿折叠得到 . 连接并延长分别交、于O、H两点,若 , 则的长度为( )
10. 如图,在正方形中, , E是的中点,F是延长线上的点,将沿折叠得到 . 连接并延长分别交、于O、H两点,若 , 则的长度为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
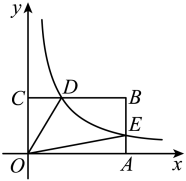
11. 不等式的最大整数解是 .12. 若关于x的一元二次方程有两个不相等的实数根,则k的取值范围是 .13. 如图,在平面直角坐标系中,矩形的顶点A,C分别在x轴,y轴的正半轴上,反比例函数的图象交于点D,交于点E.若 , , 则的值为 .
 14. 如图,在矩形中, , , 点E是对角线上一动点,连接 , 过E作 , 交边于点F,以 , 为邻边作矩形 .
14. 如图,在矩形中, , , 点E是对角线上一动点,连接 , 过E作 , 交边于点F,以 , 为邻边作矩形 .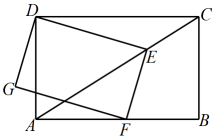 (1)、当时,则的长为;(2)、点H在上,且 , 连接 , 则长的最小值是 .
(1)、当时,则的长为;(2)、点H在上,且 , 连接 , 则长的最小值是 .三、解答题
-
15. 计算: .16. 如图,在平面直角坐标系中,三角形ABC三个顶点的坐标分别为A(-2,1),B(-3,-2),C(1,-2),若先将三角形ABC向上平移3个单位长度,再向右平移2个单位长度,得到三角形 , 请解答下列问题:
 (1)、写出点 , , 的坐标;(2)、在图中画出平移后的三角形;(3)、三角形的面积为 .17. 新冠肺炎疫情期间,某小区计划购买甲、乙两种品牌的消毒剂,甲品牌消毒剂每箱的价格比乙品牌消毒剂每箱价格的2倍少20元,已知用300元购买甲品牌消毒剂的数量与用200元购买乙品牌消毒剂的数量相同.(1)、求甲、乙两种品牌消毒剂每箱的价格各是多少元?(2)、若该小区从超市一次性购买甲、乙两种品牌的消毒剂共40箱,且总费用为2000元,求购买了多少箱乙品牌消毒剂?18. 观察以下等式:
(1)、写出点 , , 的坐标;(2)、在图中画出平移后的三角形;(3)、三角形的面积为 .17. 新冠肺炎疫情期间,某小区计划购买甲、乙两种品牌的消毒剂,甲品牌消毒剂每箱的价格比乙品牌消毒剂每箱价格的2倍少20元,已知用300元购买甲品牌消毒剂的数量与用200元购买乙品牌消毒剂的数量相同.(1)、求甲、乙两种品牌消毒剂每箱的价格各是多少元?(2)、若该小区从超市一次性购买甲、乙两种品牌的消毒剂共40箱,且总费用为2000元,求购买了多少箱乙品牌消毒剂?18. 观察以下等式:第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;…
按照以上规律,解决下列问题:
(1)、写出第6个等式:;(2)、写出你猜想的第n(n取正整数)个等式: ▲ (用含n的等式表示),并验证等式的正确性.19. 如图,AB为⊙O的直径,AC是⊙O的一条弦,点D为弧BC中点,过点D作DE⊥AC,垂足为AC的延长线上的点E.连接DA、DB. (1)、求证:DE是⊙O的切线;(2)、延长ED交AB的延长线于F,若AD=DF,DE= , 求⊙O 的半径.20. 如图,某建筑物楼顶挂有广告牌 , 小华准备利用所学的在角函数知识估测该建筑的高度.由于场地有限,不便测量,所以小华从点A处滑坡度为的斜坡步行30米到达点P处,测得广告牌底部C的仰角为45°,广告牌顶部B的仰角为53°,小华的身高忽略不计,已知广告牌米.(参考数据: , , )
(1)、求证:DE是⊙O的切线;(2)、延长ED交AB的延长线于F,若AD=DF,DE= , 求⊙O 的半径.20. 如图,某建筑物楼顶挂有广告牌 , 小华准备利用所学的在角函数知识估测该建筑的高度.由于场地有限,不便测量,所以小华从点A处滑坡度为的斜坡步行30米到达点P处,测得广告牌底部C的仰角为45°,广告牌顶部B的仰角为53°,小华的身高忽略不计,已知广告牌米.(参考数据: , , ) (1)、求P处距离水平地面的高度;(2)、求建筑物的高度.21. 双减背景下为了解学生每天回家完成作业时间情况,某中学对八年级学生每天回家完成作业时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题:
(1)、求P处距离水平地面的高度;(2)、求建筑物的高度.21. 双减背景下为了解学生每天回家完成作业时间情况,某中学对八年级学生每天回家完成作业时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题: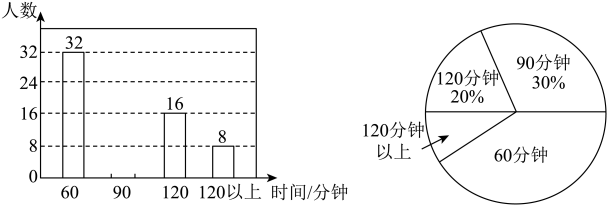 (1)、被抽样调查的学生有 ▲ 人,并补全条形统计图;(2)、每天回家完成作业时间的中位数是(分钟),众数是(分钟);(3)、该校八年级有1000名学生,请估计该校每天回家完成作业时间超过120分钟的学生有多少人?22.(1)、基础巩固:如图①,在中, , 于点 , 求证: .
(1)、被抽样调查的学生有 ▲ 人,并补全条形统计图;(2)、每天回家完成作业时间的中位数是(分钟),众数是(分钟);(3)、该校八年级有1000名学生,请估计该校每天回家完成作业时间超过120分钟的学生有多少人?22.(1)、基础巩固:如图①,在中, , 于点 , 求证: . (2)、尝试应用:如图②,在矩形中, , 点在上, , 于点 , 求的长.
(2)、尝试应用:如图②,在矩形中, , 点在上, , 于点 , 求的长. (3)、拓展提高:如图③,在矩形中,点在边上,与关于直线对称,点的对称点在边上,为中点,连接交于点 , , 若 , 求的长.
(3)、拓展提高:如图③,在矩形中,点在边上,与关于直线对称,点的对称点在边上,为中点,连接交于点 , , 若 , 求的长. 23. 某游乐场的圆形喷水池中心O有一喷水管 , 米,从A点向四周喷水,喷出的水柱为抛物线且形状相同.如图,以水平方向为x轴,点O为原点建立平面直角坐标系,点A在y轴上.已知在与池中心O点水平距离为3米时,水柱达到最高,此时高度为2米.
23. 某游乐场的圆形喷水池中心O有一喷水管 , 米,从A点向四周喷水,喷出的水柱为抛物线且形状相同.如图,以水平方向为x轴,点O为原点建立平面直角坐标系,点A在y轴上.已知在与池中心O点水平距离为3米时,水柱达到最高,此时高度为2米. (1)、求水柱所在的抛物线(第一象限部分)的函数表达式;(2)、身高为的小颖站在距离喷水管的地方,她会被水喷到吗?(3)、现重新改建喷泉,升高喷水管,使落水点与喷水管距离 , 已知喷水管升高后,喷水管喷出的水柱抛物线形状不变,且水柱仍在距离原点处达到最高,则喷水管要升高多少?
(1)、求水柱所在的抛物线(第一象限部分)的函数表达式;(2)、身高为的小颖站在距离喷水管的地方,她会被水喷到吗?(3)、现重新改建喷泉,升高喷水管,使落水点与喷水管距离 , 已知喷水管升高后,喷水管喷出的水柱抛物线形状不变,且水柱仍在距离原点处达到最高,则喷水管要升高多少?