沪科版数学七年级下册9.2分式的运算同步练习

试卷更新日期：2023-04-06 类型：同步测试

进入出卷网下载

一、单选题（每题2分，共20分）

1. 下列运算正确的是（）

A、 ${(\frac{a}{b})}^{2} = \frac{a^{2}}{b}$ B、 $a^{3} \div \frac{1}{a} = a^{4}$ C、 $\frac{- x - y}{x - y} = - 1$ D、 $\frac{1}{a} + \frac{1}{b} = \frac{2}{a + b}$

查看试题解析
2. 若把分式 $\frac{3}{x} + \frac{1}{y}$ 的x，y 同时扩大12倍，则分式的值（）

A、扩大12倍 B、缩小12倍 C、不变 D、缩小6倍

查看试题解析
3. 下列分式是最简分式的是（）

A、 $\frac{9 b}{3 a}$ B、 $\frac{a b}{2 a^{2} b}$ C、 $\frac{a + b}{a - b}$ D、 $\frac{a}{a^{2} - a b}$

查看试题解析
4. 已知 $\frac{1}{x} - \frac{1}{y} = 3$ ，则分式 $\frac{5 x + x y - 5 y}{x - x y - y}$ 的值为（）

A、8 B、 $\frac{7}{2}$ C、 $\frac{2}{7}$ D、4

查看试题解析
5. 如图、若x为正整数，则表示 $\frac{{(x - 3)}^{2}}{x^{2} - 6 x + 9} - \frac{1}{x + 1}$ 的值的点落在（）

A、① B、② C、③ D、④

查看试题解析
6. 某飞行器在相距为m的甲、乙两站间往返飞行．在没有风时，飞行器的速度为v，往返所需时间为 $t_{1}$ ；如果风速度为 $p (0 < p < v)$ ，则飞行器顺风飞行速度为 $(v + p)$ ，逆风飞行速度为 $(v - p)$ ，往返所需时间为 $t_{2}$ ．则 $t_{1}$ 、 $t_{2}$ 的大小关系为（）

A、 $t_{1} < t_{2}$ B、 $t_{1} \leq t_{2}$ C、 $t_{1} \geq t_{2}$ D、无法确定

查看试题解析

7. 在化简

\frac{2 m}{m^{2} - 4} + \frac{1}{2 - m}

时，两位同学分别给出如下方法：

佳佳的方法是：

$\begin{array}{l} \frac{2 m}{m^{2} - 4} + \frac{1}{2 - m} \\ = \frac{2 m}{m^{2} - 4} - \frac{1}{m + 2} \\ = \frac{2 m}{(m + 2) (m - 2)} - \frac{m - 2}{(m + 2) (m - 2)} \\ = \frac{2 m - m + 2}{(m + 2) (m - 2)} \\ = \frac{1}{m - 2} \end{array}$

音音的方法是：

$\begin{array}{l} \frac{2 m}{m^{2} - 4} + \frac{1}{2 - m} \\ = \frac{2 m}{(m + 2) (m - 2)} + \frac{m + 2}{(2 - m) (m + 2)} \\ = \frac{2 m}{(m + 2) (m - 2)} - \frac{m + 2}{(m - 2) (m + 2)} \\ = 2 m - m - 2 \\ = m - 2 \end{array}$

则对于两人的方法，正确的是（）

A、两人方法均正确 B、佳佳正确，音音不正确 C、佳佳不正确，音音正确 D、两人方法均不正确

查看试题解析

8. 在化简 $\frac{2 m}{m^{2} - 4} + \frac{1}{2 - m}$ 时，两位同学分别给出如下方法：则对于两人的方法，正确的是（）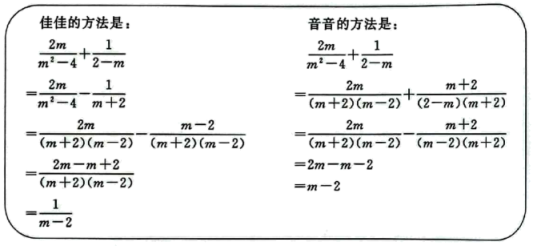

A、两人方法均正确 B、佳佳正确，音音错误 C、佳佳错误，音音正确 D、两人方法均错误

查看试题解析
9. 已知 $\frac{3 x - 4}{(x - 1) (x - 2)} = \frac{A}{x - 1} + \frac{B}{x - 2}$ ，则A，B的值分别为（）

A、A＝3，B＝﹣4 B、A＝4，B＝﹣3 C、A＝1，B＝2 D、A＝2，B＝1

查看试题解析
10. 一项工程，甲单独做需要m天完成，乙单独做需要n天完成，则甲、乙合作完成工程需要的天数为（）

A、m+n B、 $\frac{m + n}{2}$ C、 $\frac{m n}{m + n}$ D、 $\frac{m + n}{m n}$

查看试题解析

二、填空题（每空3分，共15分）

11. 计算： ${(- \frac{a}{2 b})}^{2} \div (- \frac{a^{2}}{3 b}) =$ .

查看试题解析
12. 对于代数式 $m$ ， $n$ ，定义运算“ $※$ ”： $m ※ n = \frac{m + n - 6}{mn} (mn \neq 0)$ ，例如： $4 ※ 2 = \frac{4 + 2 - 6}{4 \times 2} .$ 若 $(x - 1) ※ (x + 2) = \frac{A}{x - 1} + \frac{B}{x + 2}$ ，则 $2 A - B =$ ．

查看试题解析
13. 若 $\frac{2 x - 3}{x + 1} = A - \frac{5}{x + 1}$ ，则 $A$ 是.

查看试题解析
14. 若方程 $\frac{A}{x - 3} + \frac{B}{x + 4} = \frac{2 x + 1}{(x - 3) (x + 4)}$ ，那么A+B= ．

查看试题解析
15. 已知m﹣n＝2，则 $\frac{3 m n}{{(m + n)}^{2} - 4 m n} • (\frac{1}{m} - \frac{1}{n})$ 的值为．

查看试题解析

三、计算题（共3题，共26分）

16. 化简.

(1)、 $(- \frac{n}{m}) \div \frac{n}{m^{2} - m}$ ；

(2)、 $(\frac{1}{x - 1} - \frac{1}{x + 1}) \div \frac{x}{2 x^{2} - 2}$ .

查看试题解析
17. 先化简，再求值： $\frac{3 x + 6}{x^{2} - 6 x + 9} \div (x + 2) - \frac{x^{2} + 3 x}{x^{2} - 9} \div (x - 3)$ ，其中 $x$ 是不等式组 ${\begin{array}{l} 2 (x - 2) < 2 - x \\ \frac{x + 2}{2} > \frac{x + 3}{3} \end{array}$ 的整数解.

查看试题解析
18. 先化简，再求值： $(\frac{a^{2}}{b} - a) \div \frac{a^{2} - b^{2}}{b}$ ，其中 $a = \frac{1}{2}$ ， $b = 1$ .

查看试题解析

四、解答题（共4题，共39分）

19. 已知 $A = \frac{x^{2} - 1}{x^{2} + 2 x} - \frac{x - 1}{x}$ ， $B = 2 x^{2} + 4 x + 2$ .

(1)、化简 $A$ ，并对 $B$ 进行因式分解；

(2)、当 $B = 0$ 时，求 $A$ 的值.

查看试题解析
20. 学完分式运算后，王老师出了一道化简题： $\frac{a + 1}{a - 1} + \frac{a + 1}{1 - a^{2}}$ ，请仔细阅读下面两位同学的解题过程并完成相应的任务：

(1)、任务一：老师判断上述两位同学的解法都错误，请你分别写出他们错误的原因，小明：，小花：；

(2)、任务二：请你写出正确的化简过程．

查看试题解析
21. 阅读材料：运用公式法分解因式，除了常用的平方差公式和完全平方公式以外，还可以应用其他公式，如立方和与立方差公式，其公式如下：
立方和公式： $x^{3} + y^{3} = (x + y) (x^{2} - x y + y^{2})$ ；
立方差公式： $x^{3} - y^{3} = (x - y) (x^{2} + x y + y^{2})$ .
根据材料和已学知识解决下列问题

(1)、因式分解： $a^{3} - 8$ ；

(2)、先化简，再求值： $(\frac{3 x}{x^{2} - 2 x} - \frac{x^{2} + 2 x + 4}{x^{3} - 8}) \div \frac{2}{x^{2} - 4}$ ，其中 $x = 3$ .

查看试题解析
22. 设代数式 $M = (\frac{4}{x^{2} - 4} + \frac{1}{2 - x}) \div \frac{x - 1}{3 x + 6}$ ．

(1)、化简 $M$ ；

(2)、从 $- 2$ ， 0，1，2中选择一个合适的数代入，求 $M$ 的值．

查看试题解析