(人教版)2022-2023学年度第二学期八年级数学 特殊的平行四边形 期中复习
试卷更新日期:2023-04-06 类型:复习试卷
一、单选题
-
1. 如图,在矩形ABCD中,对角线AC、BD相交于点O,DE⊥AC于点E,∠AOD=110°,则∠CDE的大小是( )
 A、55° B、40° C、35° D、20°2. 如图,在矩形中, , 点M在边上,若平分 , 则的长是( )
A、55° B、40° C、35° D、20°2. 如图,在矩形中, , 点M在边上,若平分 , 则的长是( ) A、 B、 C、 D、3. 如图,矩形ABCD中,∠BOC=120°,BD=12,点P是AD边上一动点,则OP的最小值为( )
A、 B、 C、 D、3. 如图,矩形ABCD中,∠BOC=120°,BD=12,点P是AD边上一动点,则OP的最小值为( ) A、3 B、4 C、5 D、64. 如图,在菱形ABCD中,对角线AC、BD相交于点O,BE⊥AD于点E,且 , . 则BE的长为( )
A、3 B、4 C、5 D、64. 如图,在菱形ABCD中,对角线AC、BD相交于点O,BE⊥AD于点E,且 , . 则BE的长为( ) A、3 B、4 C、4.8 D、55. 在菱形ABCD中,相邻两内角度数之比为1:2,若它较短的对角线长度为4cm,则它的面积是( )A、16cm B、 C、 D、6. 在菱形中,对角线与相交于点O,E是的中点, , , 则的长为( )
A、3 B、4 C、4.8 D、55. 在菱形ABCD中,相邻两内角度数之比为1:2,若它较短的对角线长度为4cm,则它的面积是( )A、16cm B、 C、 D、6. 在菱形中,对角线与相交于点O,E是的中点, , , 则的长为( ) A、 B、 C、 D、7. 如图,菱形ABCD的对角线相交于点O,E是CD的中点,且OE=3,则菱形的周长是( )
A、 B、 C、 D、7. 如图,菱形ABCD的对角线相交于点O,E是CD的中点,且OE=3,则菱形的周长是( )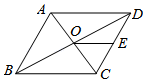 A、12 B、16 C、20 D、248. 如图,在边长为6的正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF.若DF=3,则BE的长为( )
A、12 B、16 C、20 D、248. 如图,在边长为6的正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF.若DF=3,则BE的长为( ) A、2 B、3 C、4 D、59. 如图1,直角三角形纸片的一条直角边长为1,斜边为3.把它们按图2,拼摆正方形,纸片在结合部分不重叠无缝隙,则图2的中间空白部分,即四边形ABCD的面积为( )
A、2 B、3 C、4 D、59. 如图1,直角三角形纸片的一条直角边长为1,斜边为3.把它们按图2,拼摆正方形,纸片在结合部分不重叠无缝隙,则图2的中间空白部分,即四边形ABCD的面积为( ) A、 B、9 C、 D、以上都不对10. 如图,已知四边形ABCD是平行四边形,下列结论中错误的是( )
A、 B、9 C、 D、以上都不对10. 如图,已知四边形ABCD是平行四边形,下列结论中错误的是( ) A、当AB=BC时,平行四边形ABCD是菱形 B、当AC⊥BD时,平行四边形ABCD是菱形 C、当AC=BD时,平行四边形ABCD是正方形 D、当∠ABC=90°时,平行四边形ABCD是矩形
A、当AB=BC时,平行四边形ABCD是菱形 B、当AC⊥BD时,平行四边形ABCD是菱形 C、当AC=BD时,平行四边形ABCD是正方形 D、当∠ABC=90°时,平行四边形ABCD是矩形二、填空题
-
11. 一个木匠要制作矩形的踏板.他在一个对边平行的长木板上分别沿与长边垂直的方向锯两次,就能得到矩形踏板.理由是 .
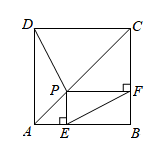
 12. 已知在中, , 点D、E分别是AC、BC的中点,连接DE,在DE上有一点F, , 连接AF,CF,若 , 则AB= .
12. 已知在中, , 点D、E分别是AC、BC的中点,连接DE,在DE上有一点F, , 连接AF,CF,若 , 则AB= .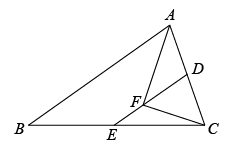 13. 如图,在四边形ABCD中,P、Q、M、N分别是AD、BC、BD、AC的中点,当四边形ABCD满足时(填写一个条件),PQ⊥MN.
13. 如图,在四边形ABCD中,P、Q、M、N分别是AD、BC、BD、AC的中点,当四边形ABCD满足时(填写一个条件),PQ⊥MN. 14. 如图,点A在线段BG上,四边形ABCD和四边形DEFG都是正方形,面积分别是10和19,则△CDE的面积为.
14. 如图,点A在线段BG上,四边形ABCD和四边形DEFG都是正方形,面积分别是10和19,则△CDE的面积为. 15. 如图,正方形ABCD的边长为4,点M在AB上,且 , N是BD上一动点,则的最小值为 .
15. 如图,正方形ABCD的边长为4,点M在AB上,且 , N是BD上一动点,则的最小值为 .
三、解答题
-
16. 如图,中, , 点E是的中点,求的长.
 17. 如图,在菱形中,对角线与相交于点 , 为的中点,过点作交的延长线于点 , 连接 . 求证:四边形是矩形.
17. 如图,在菱形中,对角线与相交于点 , 为的中点,过点作交的延长线于点 , 连接 . 求证:四边形是矩形. 18. 如图,在正方形ABCD中,AE、BF相交于点O且AF=DE.求证:∠DAE=∠ABF.
18. 如图,在正方形ABCD中,AE、BF相交于点O且AF=DE.求证:∠DAE=∠ABF.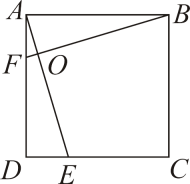
四、综合题
-
19. 如图,一块长方形场地ABCD,现测得边长AB与AD之比为∶1,DE⊥AC于点E, BF⊥AC于点F,连接BE,DF.现计划在四边形DEBF区域内种植花草.
 (1)、求证:AE=EF=CF.(2)、求四边形DEBF与矩形ABCD的面积之比.20. 如图,将两张长为10,宽为4的矩形纸条交叉叠放,使一组对角的顶点重合,其重叠部分是四边形AGCH.
(1)、求证:AE=EF=CF.(2)、求四边形DEBF与矩形ABCD的面积之比.20. 如图,将两张长为10,宽为4的矩形纸条交叉叠放,使一组对角的顶点重合,其重叠部分是四边形AGCH. (1)、证明:四边形AGCH是菱形;(2)、求菱形AGCH的周长.
(1)、证明:四边形AGCH是菱形;(2)、求菱形AGCH的周长.