(人教版)2022-2023学年度第二学期八年级数学 勾股定理的逆定理 期中复习
试卷更新日期:2023-04-06 类型:复习试卷
一、单选题
-
1. 在△ABC中,BC=a,AC=b,AB=c,根据下列条件不能判断△ABC是直角三角形的是( )A、∠B=50°,∠C=40° B、∠A=2∠B=3∠C C、a=4,b= , c=5 D、a:b:c=1::2. 下列线段a,b,c能组成直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,3. 下列数字作为三角形的三边长,不能构成直角三角形的是( )A、8,15,17 B、1, , C、4, , 3 D、 , ,4. 已知在中, , , 的对边分别记为 , , , 则下列条件不能判定为直角三角形的是( )A、 B、 C、 D、5. “赵爽弦图”巧妙利用面积关系证明勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等直角三角形和一个小正方形拼成的一个大正方形,若直角三角形较长直角边长为a,较短直角边长为b,且 , 小正方形的面积为3,则大正方形的边长为( )
 A、10 B、7 C、 D、6. 以下列线段a,b,c的长为三边的三角形中,不是直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,7. 在△ABC中, , , 的对边分别记为a,b,c,下列条件中,能判定△ABC是直角三角形的是( )A、 B、 , , C、 D、8. 我国古代数学专著《九章算数》中有一名题:“今有二人同所立,甲行率七,乙行率三.乙东行,甲南行十步而斜东北与乙会.问甲乙行各几何.”其大意是:已知甲、乙二人同时从一地出发,甲的速度为7,乙的速度为3.乙向东行走,甲先向南行走10步时偏离原方向,朝北偏东的方向直行走一段后与乙相遇.问:甲、乙各行走了多少步?设、分别为甲、乙走的路程(单位:步),则( )
A、10 B、7 C、 D、6. 以下列线段a,b,c的长为三边的三角形中,不是直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,7. 在△ABC中, , , 的对边分别记为a,b,c,下列条件中,能判定△ABC是直角三角形的是( )A、 B、 , , C、 D、8. 我国古代数学专著《九章算数》中有一名题:“今有二人同所立,甲行率七,乙行率三.乙东行,甲南行十步而斜东北与乙会.问甲乙行各几何.”其大意是:已知甲、乙二人同时从一地出发,甲的速度为7,乙的速度为3.乙向东行走,甲先向南行走10步时偏离原方向,朝北偏东的方向直行走一段后与乙相遇.问:甲、乙各行走了多少步?设、分别为甲、乙走的路程(单位:步),则( ) A、 , B、 , C、 , D、 ,9. 古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距,4个结间距,5个结间距的长度为边长,用木桩钉成一个三角形,其中一角便是直角,这样做的道理是( ).
A、 , B、 , C、 , D、 ,9. 古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距,4个结间距,5个结间距的长度为边长,用木桩钉成一个三角形,其中一角便是直角,这样做的道理是( ). A、直角三角形两个锐角互余 B、三角形的稳定性 C、勾股定理 D、勾股定理的逆定理10. 如图,正方体的棱长为2cm,点B为一条棱的中点.蚂蚁在正方体表面爬行,从点A爬到点B的最短路程是( )
A、直角三角形两个锐角互余 B、三角形的稳定性 C、勾股定理 D、勾股定理的逆定理10. 如图,正方体的棱长为2cm,点B为一条棱的中点.蚂蚁在正方体表面爬行,从点A爬到点B的最短路程是( )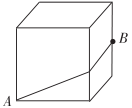 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,在△ABC中,AB=3,AC=5,AD是BC边上的中线,且AD=2,则BC的长为.
 12. 如图,已知圆柱底面的周长为 , 圆柱高为 , 在圆柱的侧面上,过点A和点C嵌有一圈红丝线,则这圈红丝线的周长最小为 .
12. 如图,已知圆柱底面的周长为 , 圆柱高为 , 在圆柱的侧面上,过点A和点C嵌有一圈红丝线,则这圈红丝线的周长最小为 . 13. 如图,一根长16cm的牙刷置于底面直径为6cm、高8cm的圆柱形水杯中,牙刷露在杯子外面的长度为hcm,则h的取值范围是 .
13. 如图,一根长16cm的牙刷置于底面直径为6cm、高8cm的圆柱形水杯中,牙刷露在杯子外面的长度为hcm,则h的取值范围是 .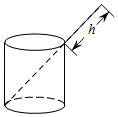 14. 如图,中, , 分别以边向外作正方形,正方形的面积为36,正方形的面积为64,则正方形的边长是 .
14. 如图,中, , 分别以边向外作正方形,正方形的面积为36,正方形的面积为64,则正方形的边长是 . 15. 如图所示,圆柱形玻璃容器,高19cm,底面周长为30cm,在外侧下底面点 处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口内侧距开口处1cm的点 处有一飞蛾,急于捕获飞蛾充饥的蜘蛛,所走的最短路线的长度是cm.(玻璃容器壁厚度忽略不计)
15. 如图所示,圆柱形玻璃容器,高19cm,底面周长为30cm,在外侧下底面点 处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口内侧距开口处1cm的点 处有一飞蛾,急于捕获飞蛾充饥的蜘蛛,所走的最短路线的长度是cm.(玻璃容器壁厚度忽略不计)
三、解答题
-
16. 在我国古代数学著作《九章算术》中记载了一个有趣的问题,这个问题的意思是:
如图,有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇沿与一边垂直的方向拉向岸边,它的顶端恰好到达岸边的水面,求池水的深度.
 17. 如图,一高层住宅发生火灾,消防车立即赶到距大厦12米(的长)处,升起云梯到火灾窗口,云梯长20米,云梯底部距地面3米(的长),问:发生火灾的住户窗口距离地面有多高(的长)?
17. 如图,一高层住宅发生火灾,消防车立即赶到距大厦12米(的长)处,升起云梯到火灾窗口,云梯长20米,云梯底部距地面3米(的长),问:发生火灾的住户窗口距离地面有多高(的长)?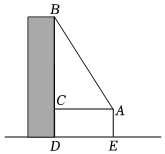 18. 《九章算术》是我国古代最重要的数学著作之一,在“勾股”章节中记载了一道“折竹抵地”的问题:“今有竹高一尺,末折抵地,去本三尺,问折者高几何?”译文为:一根竹子,原来高一丈,后来竹子折断,其竹竿恰好着地,着地处离原竹子根部3尺远,问原处还有多高的竹子?翻译成数学问题是:如图所示,△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长.
18. 《九章算术》是我国古代最重要的数学著作之一,在“勾股”章节中记载了一道“折竹抵地”的问题:“今有竹高一尺,末折抵地,去本三尺,问折者高几何?”译文为:一根竹子,原来高一丈,后来竹子折断,其竹竿恰好着地,着地处离原竹子根部3尺远,问原处还有多高的竹子?翻译成数学问题是:如图所示,△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长.
四、综合题
-
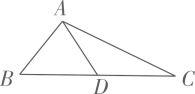
19. 如图,中,点D是上的一点, , , , .
 (1)、判断与的位置关系,并说明理由;(2)、求的面积.20. 湖的两岸有A,B两棵景观树,数学兴趣小组设计实验测量两棵景观树之间的距离,他们在与AB垂直的BC方向上取点C,测得米,米.
(1)、判断与的位置关系,并说明理由;(2)、求的面积.20. 湖的两岸有A,B两棵景观树,数学兴趣小组设计实验测量两棵景观树之间的距离,他们在与AB垂直的BC方向上取点C,测得米,米.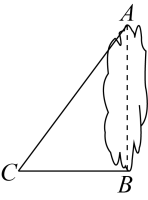
求:
(1)、两棵景观树之间的距离;(2)、点B到直线AC的距离.21. 湖的两岸有A,B两棵景观树,数学兴趣小组设计实验测量两棵景观树之间的距离,他们在与AB垂直的BC方向上取点C,测得米,米.
求:
(1)、两棵景观树之间的距离;(2)、点B到直线AC的距离.

