（人教版）2022-2023学年度第二学期八年级数学勾股定理期中复习

试卷更新日期：2023-04-06 类型：复习试卷

进入出卷网下载

一、单选题

1. 如图，传送带和地面所成斜坡的坡度为1：3，它把物体从地面点A处送到离地面3米高的B处，则物体从A到B所经过的路程为（）

A、 $3 \sqrt{10}$ 米 B、 $2 \sqrt{10}$ 米 C、 $\sqrt{10}$ 米 D、9米

查看试题解析
2. 如图，∠AOB=90°，OA=25m，OB=5m，一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O，机器人立即从点B出发，沿直线匀速前进拦截小球，恰好在点C处截住了小球，如果小球滚动的速度与机器人行走的速度相等，那么机器人行走的路程BC是（）.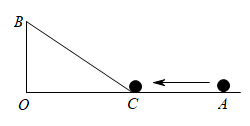

A、12米 B、13米 C、14米 D、15米

查看试题解析
3. 如图，在 $△ A B C$ 中， $B D$ 平分 $∠ A B C$ 交AC于点D，且 $B D ⊥ A C$ ， F在BC上，E为AF的中点，连接DE，若 $B F = D E$ ， $A C = 2 \sqrt{3} D E$ ， $B D = 6$ ，则AB的长为（）

A、 $3 \sqrt{6}$ B、 $4 \sqrt{3}$ C、 $\sqrt{42}$ D、9

查看试题解析
4. 如图是高空秋千的示意图，小明从起始位置点A处绕着点O经过最低点B，最终荡到最高点C处，若 $∠ A O C = 90 °$ ，点A与点B的高度差AD＝1米，水平距离BD＝4米，则点C与点B的高度差CE为（）

A、4米 B、4.5米 C、5米 D、5.5米

查看试题解析
5. 如图，在△ABC中，AB＝AC＝10，BC＝12，AD平分∠BAC，则AD等于（　　）

A、6 B、7 C、8 D、9

查看试题解析
6. 图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的.若AC＝6，BC＝5，将四个直角三角形中的边长为6的直角边分别向外延长一倍，得到图2所示的“数学风车”，则这个风车的外围周长是（）

A、51 B、49 C、76 D、无法确定

查看试题解析
7. 如图，在 $△ A B C$ 中， $∠ A B C = 90 °$ ，分别以A，C为圆心，大于 $\frac{1}{2} A C$ 长为半径作弧，两弧相交于点M，N，作直线 $M N$ ，与 $A C$ ， $B C$ 分别交于D，E，连接 $A E$ ，若 $A B = 5$ ， $A C = 13$ ，则 $△ A B E$ 的周长为（）

A、16 B、17 C、18 D、19

查看试题解析
8. 边长为5，7，8的三角形的最大角和最小角的和是（）.

A、90° B、150° C、135° D、120°

查看试题解析
9. 如图，在直线l上有正方形a，b，c，若a，c的面积分别为4和16，则b的面积为（）

A、24 B、20 C、12 D、22

查看试题解析
10. 如图所示，已知 $△ ABC$ 中， $AB = 6$ ， $AC = 9$ ， $AD ⊥ BC$ 于 $D$ ， $M$ 为 $AD$ 上任一点，则 ${MC}^{2} - {MB}^{2}$ 等于（）

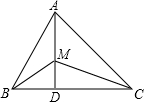A、9 B、35 C、45 D、无法计算

查看试题解析

二、填空题

11. 某人沿着坡度为 1∶2.4 的斜坡向上前进了 130m，那么他的高度上升了m.

查看试题解析
12. 如图，正方形 $A B C D$ 中，点E是 $B C$ 的中点，将正方形 $A B C D$ 沿 $A E$ 翻折，点B落在点F处，延长 $E F$ 交 $C D$ 于点P，若 $A B = 6$ ，则 $D P$ 的长为．

查看试题解析
13. 小球沿着坡度为 $i = 1 ： 1.5$ 的坡面滚动了 $13 m$ ，则在这期间小球滚动的水平距离是m．

查看试题解析
14. 如图， $△ A B C$ 与 $△ D E F$ 均为等边三角形，点 $E$ ， $F$ 在边 $B C$ 上， $B E = C F = 2 E F$ ，点 $D$ 在 $△ A B C$ 内，且 $A G = G D = G E = \sqrt{19}$ ，则 $△ A B C$ 的周长为．

查看试题解析
15. 如图，在 $△ A B C$ 中， $A C = 4$ ， $∠ A = 60 °$ ， $∠ B = 45 °$ ， $B C$ 边的垂直平分线 $D E$ 交 $A B$ 于点 $D$ ，连接 $C D$ ，则 $A B$ 的长为．

查看试题解析

三、解答题

16. 如图，笔直的公路上A、B两点相距25km，C、D为两村庄，DA⊥AB于点A，CB⊥AB于点B，已知DA＝15km，CB＝10km，现在要在公路的AB段上建一个土特产品收购站E，使得C、D两村到收购站E的距离相等，则收购站E应建在离A点多远处？

查看试题解析
17. 《九章算术》卷九“勾股”中记载：“今有立木，系索其末，委地三尺．引索却行，去本八尺而索尽．问索长几何？”译文：今有一竖立着的木柱，在木柱的上端系有绳索，绳索从木柱上端顺木柱下垂后，堆在地面的部分尚有3尺；牵着绳索（绳索与地面接触）退行，在距木柱根部8尺处时绳索用尽．问绳索长多少？即：如图，在 $R t △ A B C$ 中， $∠ A B C = 90 °$ ， $A C - A B = 3$ ， $B C = 8$ ，求 $A C$ 的长．

查看试题解析
18. 如图，某校攀岩墙 $A B$ 的顶部A处安装了一根安全绳 $A C$ ，让它垂到地面时比墙高多出了2米，教练把绳子的下端C拉开8米后，发现其下端刚好接触地面（即 $B C = 8$ 米）， $A B ⊥ B C$ ，求攀岩墙 $A B$ 的高度.

查看试题解析

四、综合题

19. 如图，直角梯形 $A B C D$ 中， $A B / / C D$ ， $∠ A D C = 90 °$ ， $A B = A C$ ，过点B作 $B E ⊥ A C$ 于点E．

(1)、求证： $△ A D C ≌ △ B E A$ ；

(2)、若 $A D = 4 ， C D = 3$ ，求 $B C$ 的长．

查看试题解析
20. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $∠ A B C = 30 °$ ， $A C = 5$ ， $A B = 10$ ，点D是射线 $C B$ 上的一个动点， $△ A D E$ 是等边三角形，点F是 $A B$ 的中点，连接 $E F$ .

(1)、如图，点D在线段 $C B$ 上时，
①求证： $△ A E F ≌ △ A D C$ ；
②连接BE，设线段 $C D = x$ ， $B E = y$ ，求 $y^{2} - x^{2}$ 的值；

(2)、当 $∠ D A B = 15 °$ 时，求 $△ A D E$ 的面积.

查看试题解析
21. 如图，在 $R t △ A B C$ 中， $∠ B = 90 °$ ， $A D$ 平分 $∠ B A C$ 交 $B C$ 于点D，作 $D E ⊥ A C$ 于点E.

(1)、若 $A D = C D$ ，求 $∠ C$ 的度数；

(2)、若 $A B = 3$ ， $A C = 5$ ，求 $△ A C D$ 的面积.

查看试题解析
22. 如图，在 $△ A B C$ 中， $∠ B A C = 60 °$ ， $∠ B = 45 °$ ， $A D$ 是 $∠ B A C$ 的平分线，且 $A C = 2 \sqrt{3}$ ， $C H ⊥ A B$ 于点 $H$ ，交 $A D$ 于点 $O$ .

(1)、求证： $△ A C D$ 是等腰三角形；

(2)、求线段 $B D$ 的长.

查看试题解析
23. 【问题背景】

(1)、如图1，点P是线段 $A B$ ， $C D$ 的中点，求证： $A C ∥ B D$ ；

(2)、【变式迁移】
如图2，在等腰 $△ A B C$ 中， $B D$ 是底边 $A C$ 上的高线，点E为 $△ A B D$ 内一点，连接 $E D$ ，延长 $E D$ 到点F，使 $E D = F D$ ，连接 $A F$ ，若 $B E ⊥ A F$ ，若 $A B = 10$ ， $E B = 6$ ，求 $A F$ 的长；

(3)、【拓展创新】
如图3，在等腰 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ，点D为 $A B$ 中点，点E在线段 $B D$ 上（点E不与点B，点D重合），连接 $C E$ ，过点A作 $A F ⊥ C E$ ，连接 $F D$ ，若 $A F = 8$ ， $C F = 3$ ，请直接写出 $F D$ 的长.

查看试题解析

（人教版）2022-2023学年度第二学期八年级数学 勾股定理 期中复习

一、单选题

二、填空题

三、解答题

四、综合题

（人教版）2022-2023学年度第二学期八年级数学勾股定理期中复习