（人教版）2022-2023学年度第二学期八年级数学二次根式期中复习

试卷更新日期：2023-04-06 类型：复习试卷

进入出卷网下载

一、单选题

1. 二次根式， x的取值可以是（）

A、1 B、0 C、－1 D、－2

查看试题解析
2. 下列计算正确的是（）

A、(－)²＝3 B、－＝3 C、(－)²＝3 D、(－)²＝－9

查看试题解析
3. 二次根式中x的取值范围是（）

A、x≥1 B、x≥－1 C、－1≤x≤1 D、x＜1

查看试题解析
4. 下面是二次根式的是（）

A、 $\frac{1}{3}$ B、-3 C、 $\sqrt{2}$ D、 $\sqrt{- 4}$

查看试题解析
5. 要使式子 $\frac{3}{\sqrt{6 - 2 x}}$ 在实数范围内有意义，则x的取值范围是（）

A、 $x < 3$ B、 $x \geq 3$ C、 $x \leq 3$ D、 $x \neq 3$

查看试题解析
6. 实数a、b在数轴上的位置如图，则化简 $\sqrt{(a - b)^{2}}$ 的结果是（）

A、 $a + b$ B、 $a - b$ C、 $- a + b$ D、 $- a - b$

查看试题解析
7. 如果 $a$ 是任意实数，下列各式中一定有意义的是（）

A、 $\sqrt{a}$ B、 $\sqrt{- a^{2}}$ C、 $\sqrt{\frac{1}{a^{2}}}$ D、 $\sqrt{a^{2} + 1}$

查看试题解析
8. 当 $x > 2$ 时， $\sqrt{{(2 - x)}^{2}}$ = （）

A、 $2 - x$ B、 $x - 2$ C、 $2 + x$ D、 $\pm (x - 2)$

查看试题解析
9. 若 $\sqrt{a^{2} b} = a \sqrt{b}$ 成立，则a，b满足的条件是（）

A、 $a < 0$ 且 $b > 0$ B、 $a \geq 0$ 且 $b \geq 0$ C、 $a < 0$ 且 $b \geq 0$ D、a，b异号

查看试题解析
10. 二次根式 $\sqrt{a}$ 的最小值为（）

A、0 B、1 C、 $- 1$ D、不能确定

查看试题解析

二、填空题

11. 若 $\sqrt{2 - x} + \sqrt{x - 2} + y = 4$ ，则 $x^{y}$ =.

查看试题解析
12. 若 $\sqrt{x - 1}$ 在实数范围内有意义，则 $x$ 的取值范围为.

查看试题解析
13. 已知 $y =$ $\sqrt{x - 2} + \sqrt{2 - x} - \frac{1}{2}$ ，则 $x^{2021} \cdot y^{2020} =$ .

查看试题解析
14. 化简＝．

查看试题解析
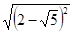15. 若代数式 $\sqrt{2 x - 8}$ 有意义，则实数x的取值范围是．

查看试题解析

三、解答题

16. 已知 $(m - 3) \sqrt{m - 2}$ ≤0，若整数k满足m+k＝ $3 \sqrt{2}$ ．试求k的值．

查看试题解析
17. 已知实数x、y满足， $y = \frac{\sqrt{x^{2} - 4} + \sqrt{4 - x^{2}}}{x - 2} + 3$ ，求9x＋8y的值.

查看试题解析
18. 古希腊的几何学家海伦给出了求三角形面积的公式：S= $\sqrt{p (p - a) (p - b) (p - c)}$ ，其中a，b，c为三角形的三边长，p= $\frac{a + b + c}{2}$ ．若一个三角形的三边长分别为2，3，4，求该三角形的面积．

查看试题解析

四、综合题

19. 阅读理解题，下面我们观察：
$(\sqrt{2} - 1)^{2} = (\sqrt{2})^{2} - 2 \times 1 \times \sqrt{2} + 1^{2} = 2 - 2 \sqrt{2} + 1 = 3 - 2 \sqrt{2}$ .反之 $3 - 2 \sqrt{2} = 2 - 2 \sqrt{2} + 1 = (\sqrt{2} - 1)^{2} ，$ 所以 $3 - 2 \sqrt{2} = (\sqrt{2} - 1)^{2} ，$ 所以 $\sqrt{3 - 2 \sqrt{2}} = \sqrt{2} - 1$ .

完成下列各题：

(1)、把 $3 + 2 \sqrt{2}$ 写成 ${(a + b)}^{2}$ 的形式；

(2)、化简： $\sqrt{4 + 2 \sqrt{3}}$ ；

(3)、化简： $\sqrt{5 - 2 \sqrt{6}}$ .

查看试题解析
20. 有这样一道题：先化简，再求值：a+ $\sqrt{1 - 2 a + a^{2}}$ ，其中a＝1000．小亮和小芳分别给出了不同的解答过程．
小亮的解答是：原式＝a+ $\sqrt{(1 - a)^{2}}$ ＝a+1-a＝1．
小芳的解答是：原式＝a+ $\sqrt{(1 - a)^{2}}$ ＝a-（1-a）＝2a-1＝2×1000-1＝1999．

(1)、的解答是错误的；

(2)、先化简，再求值：a+2 $\sqrt{a^{2} - 6 a + 9}$ ，其中a＝-200．

查看试题解析
21. 如图，一只蚂蚁从点A沿数轴向右直爬2个单位长度到达点B，点A表示－，设点B所表示的数为m.

(1)、求m的值；

(2)、求|m－1|＋(m＋ $\sqrt{2}$ )²的值．

查看试题解析
22. 问题探究：因为 $(\sqrt{2} - 1)^{2} = 3 - 2 \sqrt{2}$ ，所以 $\sqrt{3 - 2 \sqrt{2}} = \sqrt{2} - 1 ，$
因为 $(\sqrt{2} + 1)^{2} = 3 + 2 \sqrt{2}$ ，所以 $\sqrt{3 + 2 \sqrt{2}} = \sqrt{2} + 1 ，$ 因为 $(2 - \sqrt{3})^{2} = 7 - 4 \sqrt{3}$ ，所以 $\sqrt{7 - 4 \sqrt{3}} = 2 - \sqrt{3} ，$ 请你根据以上规律，结合你的经验化简下列各式：

(1)、 $\sqrt{5 - 2 \sqrt{6}}$ ；

(2)、 $\sqrt{\frac{9}{4} + \sqrt{2}} \cdot$

查看试题解析
23. 小明在学习二次根式时，碰到这样一道题，他尝试着运用分类讨论的方法解题如下：
题目：若代数式 $\sqrt{{(m - 1)}^{2}} + \sqrt{{(m - 2)}^{2}}$ 的值是1，求 $m$ 的取值范围.

解：原式 $= | m - 1 | + | m - 2 |$ ，

当 $m < 1$ 时，原式 $= (1 - m) + (2 - m) = 3 - 2 m = 1$ ，解得 $m = 1$ （舍去）；

当 $1 \leq m \leq 2$ 时，原式 $= (m - 1) + (2 - m) = 1$ ，符合条件；

当 $m > 2$ 时，原式 $= (m - 1) + (m - 2) = 2 m - 3 = 1$ ，解得 $m = 2$ （舍去）；

所以， $m$ 的取值范围是 $1 \leq m \leq 2$ .

请你根据小明的做法，解答下列问题：

(1)、当 $3 \leq m \leq 5$ 时，化简： $\sqrt{{(m - 3)}^{2}} + \sqrt{{(m - 5)}^{2}} =$ ；

(2)、若代数式 $\sqrt{{(2 - m)}^{2}} - \sqrt{{(m - 6)}^{2}}$ 的值是4，求 $m$ 的取值范围.

查看试题解析

（人教版）2022-2023学年度第二学期八年级数学 二次根式 期中复习

一、单选题

二、填空题

三、解答题

四、综合题

（人教版）2022-2023学年度第二学期八年级数学二次根式期中复习