广西玉林地区2021-2022学年七年级下学期期中考试数学试题
试卷更新日期:2023-04-06 类型:期中考试
一、单选题
-
1. 小明读了“子非鱼,安知鱼之乐?”后,兴高采烈地利用电脑画出了几幅鱼的图案.由图所示的图案通过平移后得到的图案是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 点P(2,-3)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 在 , 3.14, , -8,1.010010001…, , , 中,无理数的个数有( )A、2个 B、3个 C、4个 D、5个4. 下面四个图形中, 与 是邻补角的是( )A、
2. 点P(2,-3)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 在 , 3.14, , -8,1.010010001…, , , 中,无理数的个数有( )A、2个 B、3个 C、4个 D、5个4. 下面四个图形中, 与 是邻补角的是( )A、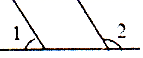 B、
B、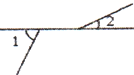 C、
C、 D、
D、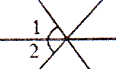 5. 下列说法正确的是( ).A、是的平方根 B、2是的算术平方根 C、的平方根是2 D、8的立方根是6. 如图,AB∥DF,AC⊥CE于C,BC与DF交于点E,若∠A=20°,则∠CEF等于( )
5. 下列说法正确的是( ).A、是的平方根 B、2是的算术平方根 C、的平方根是2 D、8的立方根是6. 如图,AB∥DF,AC⊥CE于C,BC与DF交于点E,若∠A=20°,则∠CEF等于( )
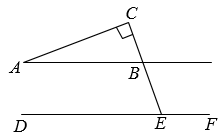 A、110° B、100° C、80° D、70°7. 下列实数中,在3与4之间的数是( )A、 B、 C、 D、8. 下列命题中是真命题的是( )A、两条直线被第三条直线所截,内错角相等 B、相等的角是对顶角 C、若 , 则 D、平方根是本身的数只有09. 如图,A是直线l外一点,过点A作AB⊥l于点B , 在直线l上取一点C , 连接 , , P在线段BC上,连接AP.若AB=3,则线段AP的长不可能是( )
A、110° B、100° C、80° D、70°7. 下列实数中,在3与4之间的数是( )A、 B、 C、 D、8. 下列命题中是真命题的是( )A、两条直线被第三条直线所截,内错角相等 B、相等的角是对顶角 C、若 , 则 D、平方根是本身的数只有09. 如图,A是直线l外一点,过点A作AB⊥l于点B , 在直线l上取一点C , 连接 , , P在线段BC上,连接AP.若AB=3,则线段AP的长不可能是( ) A、3 B、4 C、5.5 D、6.510. 如图,点E在的延长线上,则下列条件中,不能判定的是( )
A、3 B、4 C、5.5 D、6.510. 如图,点E在的延长线上,则下列条件中,不能判定的是( ) A、 B、 C、 D、11. 实数a在数轴上的位置如图所示,则 化简后为( )
A、 B、 C、 D、11. 实数a在数轴上的位置如图所示,则 化简后为( )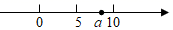 A、9 B、﹣9 C、2a﹣15 D、无法确定12. 如图,AB∥CD , OE平分∠BOC , OF⊥OE , OP⊥CD , ∠ABO=40°,则下列结论:①∠BOE=70°;②OF平分∠BOD;③∠1=∠2;④∠POB=2∠3.其中正确的结论有( )
A、9 B、﹣9 C、2a﹣15 D、无法确定12. 如图,AB∥CD , OE平分∠BOC , OF⊥OE , OP⊥CD , ∠ABO=40°,则下列结论:①∠BOE=70°;②OF平分∠BOD;③∠1=∠2;④∠POB=2∠3.其中正确的结论有( ) A、①④ B、②④ C、①②③ D、①③④
A、①④ B、②④ C、①②③ D、①③④二、填空题
-
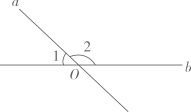
13. -27的立方根是.14. 如图所示直线a,b相交于点O, , 则.
 15. 如图,已知棋子“车”的坐标为(-2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为.
15. 如图,已知棋子“车”的坐标为(-2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为. 16. 如图,小明在学习平行线的性质后,把含有角的直角三角板摆放在自己的文具上, , 若 , 则.
16. 如图,小明在学习平行线的性质后,把含有角的直角三角板摆放在自己的文具上, , 若 , 则. 17. 已知直线AB∥y轴,点A的坐标为(1,2),并且线段AB=3,则点B的坐标为.18. 任何实数a,可用表示不超过a的最大整数,如 , 现对72进行如下操作: , 这样对72只需进行3次操作后变为1,类似地,①对81只需进行次操作后变为1;②只需进行3次操作后变为1的所有正整数中,最大的是 .
17. 已知直线AB∥y轴,点A的坐标为(1,2),并且线段AB=3,则点B的坐标为.18. 任何实数a,可用表示不超过a的最大整数,如 , 现对72进行如下操作: , 这样对72只需进行3次操作后变为1,类似地,①对81只需进行次操作后变为1;②只需进行3次操作后变为1的所有正整数中,最大的是 .三、解答题
-
19. 计算: .20. 求下列各式中的x.(1)、(2)、21. 如图,∠1+∠2=180°,∠B=∠3.
 (1)、求证:DE∥BC.(2)、若∠C=76°,求∠DEC的度数.22. 完成下面的解题过程.
(1)、求证:DE∥BC.(2)、若∠C=76°,求∠DEC的度数.22. 完成下面的解题过程.已知:如图, , 平分 , 求.

解:∵(对顶角相等)
又∵
∴
∴( )
∴_▲ ( )
∵
∴
∵平分
∴_▲_=_▲_
∴_▲_.
23. 如图,在平面直角坐标系中,的三个顶点的坐标分别是 , , . (1)、求出的面积;(2)、平移 , 若点A的对应点的坐标为 , 画出平移后对应的 , 并写出点、的坐标.24. 已知5a+2的立方根是3,3a+b-1的算术平方根是4,c是的整数部分.(1)、求a,b,c的值;(2)、求3a-b+c的平方根.25. 如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3,∠2=∠4.
(1)、求出的面积;(2)、平移 , 若点A的对应点的坐标为 , 画出平移后对应的 , 并写出点、的坐标.24. 已知5a+2的立方根是3,3a+b-1的算术平方根是4,c是的整数部分.(1)、求a,b,c的值;(2)、求3a-b+c的平方根.25. 如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3,∠2=∠4.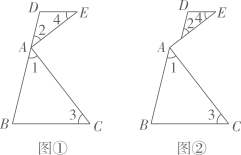 (1)、如图①,求证:DE∥BC;(2)、若将图①改变为图②,其他条件不变,(1)中的结论是否仍成立?请说明理由.26. 如图,已知点满足.将线段先向上平移2个单位,再向右平移1个单位后得到线段 , 并连接.
(1)、如图①,求证:DE∥BC;(2)、若将图①改变为图②,其他条件不变,(1)中的结论是否仍成立?请说明理由.26. 如图,已知点满足.将线段先向上平移2个单位,再向右平移1个单位后得到线段 , 并连接. (1)、请求出点A和点B的坐标;(2)、点M从O点出发,以每秒1个单位的速度向上平移运动.设运动时间为t秒,问:是否存在这样的t,使得四边形的面积等于9?若存在,请求出t的值:若不存在,请说明理由;(3)、在(2)的条件下,点M从O点出发的同时,点N从点B出发,以每秒2个单位的速度向左平移运动,设射线交y轴于点E.设运动时间为t秒,问:的值是否会发生变化?若不变,请求出它的值:若变化,请说明理由.
(1)、请求出点A和点B的坐标;(2)、点M从O点出发,以每秒1个单位的速度向上平移运动.设运动时间为t秒,问:是否存在这样的t,使得四边形的面积等于9?若存在,请求出t的值:若不存在,请说明理由;(3)、在(2)的条件下,点M从O点出发的同时,点N从点B出发,以每秒2个单位的速度向左平移运动,设射线交y轴于点E.设运动时间为t秒,问:的值是否会发生变化?若不变,请求出它的值:若变化,请说明理由.