浙江省宁波市海曙区部分校2022-2023学年七年级下学期3月月考数学试题

试卷更新日期：2023-04-06 类型：月考试卷

进入出卷网下载

一、单选题

1. 观察下面图案，在A，B，C，D四幅图案中，能通过图1平移得到的是（）

A、 B、 C、 D、

查看试题解析
2. 下列四个图形中， $∠ 1$ 与 $∠ 2$ 互为内错角的是（）

A、 B、 C、 D、

查看试题解析
3. 下列方程组中是二元一次方程组的是（）

A、 ${\begin{array}{l} x + y = 4 \\ x - y = 1 \end{array}$ B、 ${\begin{array}{l} 4 x + 3 y = 6 \\ 2 y + z = 4 \end{array}$ C、 ${\begin{array}{l} x + y = 5 \\ x^{2} + y^{2} = 13 \end{array}$ D、 ${\begin{array}{l} \frac{1}{x} + y = 4 \\ x - y = 1 \end{array}$

查看试题解析
4. 如图，下列推理中，正确的是（）

A、如果 $∠ 2 = ∠ 4$ ，那么 $A D ∥ B C$ B、如果 $∠ 1 = ∠ 3$ ，那么 $A D ∥ B C$ C、如果 $∠ 4 + ∠ D = 180 °$ ，那么 $A D ∥ B C$ D、如果 $∠ 4 + ∠ B = 180 °$ ，那么 $A B ∥ D C$

查看试题解析
5. 已知 ${\begin{array}{l} x = 1 \\ y = 3 \end{array}$ 是关于 $x$ ， $y$ 的二元一次方程 $x - 2 y = m$ 的一个解，则 $m$ 的值是（）

A、5 B、2 C、-5 D、-2

查看试题解析
6. 如图，将三角形 $A B C$ 沿射线 $A B$ 平移到三角形 $D E F$ 的位置，则下列说法不正确的是（）

A、 $A C = D B$ B、 $A D = B E$ C、 $A C ∥ D F$ D、 $∠ C = ∠ F$

查看试题解析
7. 根据大马和小马的对话求大马和小马各驮了几包货物．
大马说：“把我驮的东西给你1包多好哇！这样咱俩驮的包数就一样多了．”
小马说：“我还想给你1包呢！”
大马说：“那可不行！如果你给我1包，我驮的包数就是你的2倍了．”
小明将这个实际问题转化为二元一次方程组问题．设未知数x，y，已经列出一个方程x-1＝y+1，则另一个方程应是（）

A、x+1＝2y B、x+1＝2（y-1） C、x-1＝2（y-1） D、y＝1-2x

查看试题解析
8. 如图，将一块三角板的直角顶点放在直尺的一边上，当 $∠ 1 = 50 °$ 时，则 $∠ 2$ 的度数为（）

A、 $130 °$ B、 $100 °$ C、 $50 °$ D、 $40 °$

查看试题解析
9. 小明在解关于x，y的二元一次方程组 ${\begin{array}{l} x + m y = 3 \\ 3 x - m y = 1 \end{array}$ 时，得到了正确的结果 ${\begin{array}{l} x = n \\ y = 1 \end{array}$ ，后来发现“m”“n”处被墨水污损了，请你帮他找出m，n处的值分别是（）

A、m=1，n=1 B、m=2，n=1 C、m=1，n=2 D、m=2，n=2

查看试题解析
10. 用如图①中的长方形和正方形纸板作侧面和底面，做成如图②的竖式和横式的两种无盖纸盒现在仓库里有m张正方形纸板和n张长方形纸板，如果做两种纸盒若干个，恰好使库存的纸板用完，则 $m + n$ 的值可能是（）

A、2023 B、2024 C、2025 D、2026

查看试题解析

二、填空题

11. 若 $(a - 2) x^{| a | - 1} + 3 y = 1$ 是关于x、y的二元一次方程，则a=.

查看试题解析
12. 已知方程 $2 x = 3 y + 7$ ，用含y的代数式表示x为.

查看试题解析
13. 如图，直线a、b被c所截， $∠ 1 = 130 °$ ，当 $∠ 2 =$ °时， $a ∥ b$

查看试题解析
14. 如图，直线l₁ $∥$ l₂ ，若∠1＝35°，则∠2+∠3＝.

查看试题解析
15. 图，三角形 $A B C$ 中， $∠ A B C = 90 °$ ，将三角形 $A B C$ 沿 $A B$ 方向平移 $A D$ 的长度得到三角形 $D E F$ ，且 $E F = 8$ ， $A D = 4$ ， $C G = 3$ ，则图中阴影部分的面积是.

查看试题解析
16. 如图，七个相同的小长方形组成一个大长方形 $A B C D$ ，若 $C D = 21$ ，则长方形 $A B C D$ 的周长为.

查看试题解析
17. 如图，将一张长方形纸片进行折叠，若 $∠ 2 - ∠ 1 = 20 °$ ，则 $∠ E F C$ 的度数为.

查看试题解析
18. 若方程组 ${\begin{array}{l} 2 a - 3 b = 13 \\ 3 a + 5 b = 30.9 \end{array}$ 解为 ${\begin{array}{l} a = 8.3 \\ b = 1.2 \end{array}$ ，则方程组 ${\begin{array}{l} 2 (x + 2) - 3 (y - 1) = 13 \\ 3 (x + 2) + 5 (y - 1) = 30.9 \end{array}$ 的解为.

查看试题解析

三、解答题

19. 解方程组：

(1)、 ${\begin{array}{l} x = 2 y \\ 3 x - 2 y = 8 \end{array}$

(2)、 ${\begin{array}{l} 3 x + 2 y = 4 \\ \frac{x}{2} - \frac{y + 1}{3} = 1 \end{array}$

查看试题解析
20. 如图，已知 $∠ 1 = ∠ 2$ ， $∠ A = ∠ D$ .

(1)、判断 $A B$ 与 $C D$ 的位置关系，并说明理由

(2)、若 $∠ B F D = 40 °$ ，求 $∠ M E C$ 的度数

查看试题解析
21. 已知关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} x + 2 y - 6 = 0 \\ x - 2 y + m x + 5 = 0 \end{array}$ .

(1)、请直接写出方程 $x + 2 y = 6$ 的所有正整数解；

(2)、若方程组的解满足 $x + y = 0$ ，求 $m$ 的值；

(3)、无论实数 $m$ 取何值，方程 $x - 2 y + m x + 5 = 0$ 总有一个固定的解，请直接写出这个解.

查看试题解析
22. 为了保护环境，某市公交公司决定购买一批共10台全新的混合动力公交车，现有 $A 、 B$ 两种型号，其中每台的价格，年省油量如下表：

A
B
价格（万元/台）
a
b
节省的油量（万升/年）
2.4
2
经调查，购买一台A型车比购买一台B型车多20万元，购买2台A型车比购买3台B型车少60万元.

(1)、请求出a和b；

(2)、若购买这批混合动力公交车每年能节省22.4万升汽油，求购买这批混合动力公交车需要多少万元?

查看试题解析
23. 已知点C在射线OA上.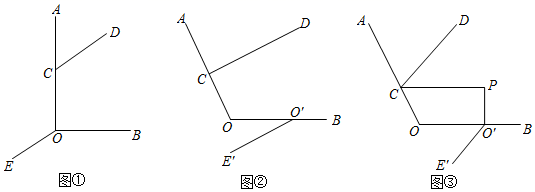

(1)、如图①，CD $//$ OE，若∠AOB＝90°，∠OCD＝120°，求∠BOE的度数；

(2)、在①中，将射线OE沿射线OB平移得O′E'（如图②），若∠AOB＝α，探究∠OCD与∠BO′E′的关系（用含α的代数式表示）

(3)、在②中，过点O′作OB的垂线，与∠OCD的平分线交于点P（如图③），若∠CPO′＝90°，探究∠AOB与∠BO′E′的关系.

查看试题解析

	A	B
价格（万元/台）	a	b
节省的油量（万升/年）	2.4	2