陕西省西安市多校2022-2023学年八年级下学期第一次月考数学试卷
试卷更新日期:2023-04-06 类型:月考试卷
一、单选题
-
1. 交通法规人人遵守,文明城市处处安全.在通过桥洞时,我们往往会看到下图所示的标志,这是限制车高的标志,则通过该桥洞的车高的范围可表示为( )
 A、 B、 C、 D、2. 下列变形正确的是( )A、由 , 得 B、由 , 得 C、由 , 得 D、由 , 得3. 如图,在中,边上的垂直平分线分别交边于点 , 交边于点 , 若的长为 , 的长为 , 则的长为( )
A、 B、 C、 D、2. 下列变形正确的是( )A、由 , 得 B、由 , 得 C、由 , 得 D、由 , 得3. 如图,在中,边上的垂直平分线分别交边于点 , 交边于点 , 若的长为 , 的长为 , 则的长为( )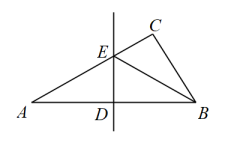 A、 B、 C、 D、4. 若是关于的一元一次不等式.则的值为( )A、2 B、-1 C、0 D、0或25. 已知等腰三角形的两边 , 满足 , 则等腰三角形的周长为( )A、12 B、16 C、20 D、16或206. 如图,在中, , , , 是边上的动点,则的长不可能是( )
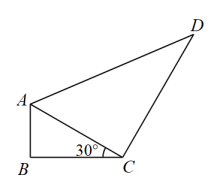
A、 B、 C、 D、4. 若是关于的一元一次不等式.则的值为( )A、2 B、-1 C、0 D、0或25. 已知等腰三角形的两边 , 满足 , 则等腰三角形的周长为( )A、12 B、16 C、20 D、16或206. 如图,在中, , , , 是边上的动点,则的长不可能是( ) A、3 B、5 C、6 D、77. 如图,在中, , , , 将折叠,使边落在边上,展开后得到折痕 , 则的长度为( )
A、3 B、5 C、6 D、77. 如图,在中, , , , 将折叠,使边落在边上,展开后得到折痕 , 则的长度为( ) A、2 B、 C、 D、8. 如图,的角平分线 , 交于点 , , 的面积为16,四边形的面积为5,则的面积为( )
A、2 B、 C、 D、8. 如图,的角平分线 , 交于点 , , 的面积为16,四边形的面积为5,则的面积为( ) A、5 B、5.5 C、6 D、7
A、5 B、5.5 C、6 D、7二、填空题
-
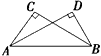
9. 由x<y得到ax>ay,则a的取值范围是 .10. 如图,AC⊥BC,AD⊥BD,垂足分别是C、D,若要用“HL”得到Rt△ABC≌Rt△BAD,则你添加的条件是.(写一种即可)
 11. 如图1,一个容量为的杯子中装有的水,将五颗相同的玻璃球放入这个杯子中(如图2),结果水没有满.设每颗玻璃球的体积为.请列出不等式:.
11. 如图1,一个容量为的杯子中装有的水,将五颗相同的玻璃球放入这个杯子中(如图2),结果水没有满.设每颗玻璃球的体积为.请列出不等式:. 12. 命题“线段垂直平分线上的任意一点,到这条线段两个端点距离相等”的逆命题是 .13. 如图, , 平分 , 于点 , , 已知 , 则.
12. 命题“线段垂直平分线上的任意一点,到这条线段两个端点距离相等”的逆命题是 .13. 如图, , 平分 , 于点 , , 已知 , 则.
三、解答题
-
14. 解不等式: , 并将解集在数轴上表示出来.15. 如图,在中, , , 的垂直平分线交边于点 , 交边于点 , 连接 , 求的度数.
 16. 如图,已知 , , 垂足是的中点.求证:.
16. 如图,已知 , , 垂足是的中点.求证:.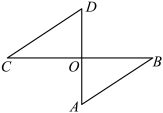 17. 如图,已知线段AB.用尺规作图的方法作出线段AB的垂直平分线MN(保留作图痕迹,不要求写出作法);
17. 如图,已知线段AB.用尺规作图的方法作出线段AB的垂直平分线MN(保留作图痕迹,不要求写出作法); 18. 如图,已知是直线上一点,是从点引出的一条射线.且.若是的平分线,且满足 , 求的度数.
18. 如图,已知是直线上一点,是从点引出的一条射线.且.若是的平分线,且满足 , 求的度数.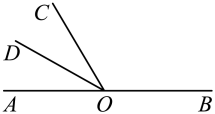 19. 已知等腰三角形的三边长分别为 , , 8,求等腰三角形的周长.20. 在元旦前夕,某商场为儿童推出一款特价商品,某超市为了促销这种定价为4元/件的商品,采取下列方式优惠销售:若一次性购买不超过3件,按原价付款;若一次性购买超过3件,则超过的部分按原价八折付款.如果小明有40元钱,那么他最多可以购买多少件这种商品?21. 如图, , 为边上一点.且 , .求证:
19. 已知等腰三角形的三边长分别为 , , 8,求等腰三角形的周长.20. 在元旦前夕,某商场为儿童推出一款特价商品,某超市为了促销这种定价为4元/件的商品,采取下列方式优惠销售:若一次性购买不超过3件,按原价付款;若一次性购买超过3件,则超过的部分按原价八折付款.如果小明有40元钱,那么他最多可以购买多少件这种商品?21. 如图, , 为边上一点.且 , .求证: (1)、.(2)、.22. 定义新运算:对于任意实数 , , 都有.比如:.(1)、求的值.(2)、若的值小于7,求的取值范围.23. 如图,在中, , 于点 , 是的外角的平分线.
(1)、.(2)、.22. 定义新运算:对于任意实数 , , 都有.比如:.(1)、求的值.(2)、若的值小于7,求的取值范围.23. 如图,在中, , 于点 , 是的外角的平分线. (1)、求证:.(2)、若平分交于点 , 判断的形状并说明理由.24. 【阅读】根据等式和不等式的基本性质,我们可以得到比较两数大小的方法:
(1)、求证:.(2)、若平分交于点 , 判断的形状并说明理由.24. 【阅读】根据等式和不等式的基本性质,我们可以得到比较两数大小的方法:若 , 则;
若 , 则;
若 , 则.
反之也成立.
这种比较大小的方法称为“作差法比较大小”.
(1)、【理解】若 , 则(填“”、“”或“”)(2)、【运用】若 , , 试比较 , 的大小.(3)、【拓展】请运用“作差法比较大小”解决下面这个问题.制作某产品有两种用料方案,方案一:用5块A型钢板,6块型钢板.方案二:用4块A型钢板,7块型钢板.每块A型钢板的面积比每块型钢板的面积小.方案一的总面积记为 , 方案二的总面积记为 , 试比较 , 的大小.