江苏省苏州市吴中、吴江、相城区2023年九年级数学第一次调研试题
试卷更新日期:2023-04-06 类型:中考模拟
一、单选题
-
1. 3的相反数为( )A、 ﹣3 B、﹣ C、 D、32. 苏州是全国最大工业城市之一,2022年苏州工业总产值大约为万元,数据用科学记数法可表示为( )A、 B、 C、 D、3. 苏州的景色非常优美,其中以苏州园林最具代表性.苏州园林溯源于春秋,发展于晋唐,繁荣于两宋,全胜于明清,现存五十多处.如图是苏州园林中的一种窗格,下面从窗格图案中提取的几何图形,不一定是轴对称图形的是( )
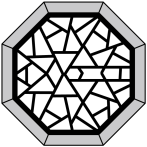 A、矩形 B、正八边形 C、平行四边形 D、等腰三角形4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,是的直径,是的弦,过点的切线交的延长线于点.若 , 则的度数为( )
A、矩形 B、正八边形 C、平行四边形 D、等腰三角形4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,是的直径,是的弦,过点的切线交的延长线于点.若 , 则的度数为( )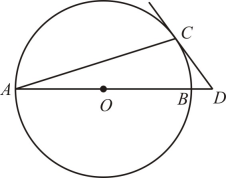 A、 B、 C、 D、6. “孔子周游列国”是流传很广的故事.有一次他和学生到离他们住的驿站30里的书院参观,学生步行出发1小时后,孔子坐牛车出发,牛车的速度是步行的倍,孔子和学生们同时到达书院,设学生步行的速度为每小时里,则可列方程为( )A、 B、 C、 D、7. 如图,点是正五边形的中心,过点作 , 垂足为 , 则下列四个选项中正确的为( )
A、 B、 C、 D、6. “孔子周游列国”是流传很广的故事.有一次他和学生到离他们住的驿站30里的书院参观,学生步行出发1小时后,孔子坐牛车出发,牛车的速度是步行的倍,孔子和学生们同时到达书院,设学生步行的速度为每小时里,则可列方程为( )A、 B、 C、 D、7. 如图,点是正五边形的中心,过点作 , 垂足为 , 则下列四个选项中正确的为( )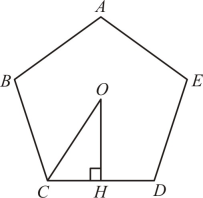 A、 B、 C、 D、8. 如图,在中, , .动点从点出发,沿线段以1单位长度/秒的速度运动,当点与点重合时,整个运动停止.以为一边向上作正方形 , 若设运动时间为秒 , 正方形与重合部分的面积为 , 则下列能大致反映与的函数关系的图像是( )
A、 B、 C、 D、8. 如图,在中, , .动点从点出发,沿线段以1单位长度/秒的速度运动,当点与点重合时,整个运动停止.以为一边向上作正方形 , 若设运动时间为秒 , 正方形与重合部分的面积为 , 则下列能大致反映与的函数关系的图像是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
9. 计算:.10. 在辽宁号航母的某次出海训练中,某飞行大队8架舰载机的飞行训练次数如下(单位:次):7,6,6,4,5,6,7,5,这组数据的众数是.11. 如图,在的正方形网格飞镖游戏板中,每块小正方形除颜色外都相同,小正方形的顶点称为格点.假设飞镖击中每一块小正方形是等可能的,任意投掷飞镖一次,飞镖击中阴影部分的概率是.
 12. 因式分解 = .13. 定义:如果三角形的一个内角是另一个内角的2倍,那么称这个三角形为“倍角三角形”.若是“倍角三角形”, , , 则的面积为.14. 已知二次函数 , 当时,的最小值为 , 则的值为.15. 如图,在矩形中, , , 是上一个动点,过点作 , 垂足为 , 连接 , 取中点 , 连接 , 则线段的最小值为.
12. 因式分解 = .13. 定义:如果三角形的一个内角是另一个内角的2倍,那么称这个三角形为“倍角三角形”.若是“倍角三角形”, , , 则的面积为.14. 已知二次函数 , 当时,的最小值为 , 则的值为.15. 如图,在矩形中, , , 是上一个动点,过点作 , 垂足为 , 连接 , 取中点 , 连接 , 则线段的最小值为.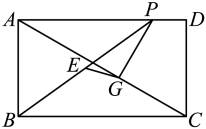
三、解答题
-
16. 计算:.17. 解不等式组:并把它的解集在数轴上表示出来.18. 先化简: , 然后从2,0,中选一个合适的数代入求值.19. 第19届亚运会将于2023年9月23日至10月8日在杭州举行,杭州亚运会吉祥物是“宸宸”、“琮琮”和“莲莲”.将三张正面分别印有以上3个吉祥物图案的卡片(卡片的形状、大小、质地都相同)背面朝上、洗匀.
 (1)、若从中任意抽取1张,抽得卡片上的图案恰好为“莲莲”的概率是.(2)、若先从中任意抽取1张,记录后放回,洗匀,再从中任意抽取1张,求两次抽取的卡片图案不同的概率.(请用树状图或列表的方法求解)20. 如图,在中,为的中点,连接并延长,交的延长线于点.
(1)、若从中任意抽取1张,抽得卡片上的图案恰好为“莲莲”的概率是.(2)、若先从中任意抽取1张,记录后放回,洗匀,再从中任意抽取1张,求两次抽取的卡片图案不同的概率.(请用树状图或列表的方法求解)20. 如图,在中,为的中点,连接并延长,交的延长线于点. (1)、求证:;(2)、若 , 求的长.21. 阅读是人类获取知识、启智增慧、培养道德的重要途经,可以让人得到思想启发,树立崇高理想,涵养浩然之气.某初级中学为了解学生近两周平均每天在家阅读时长(单位:小时)的情况,从本校学生中随机抽取了部分学生进行问卷调查,并将结果绘制成如下不完整的频数分布直方图和扇形统计图.
(1)、求证:;(2)、若 , 求的长.21. 阅读是人类获取知识、启智增慧、培养道德的重要途经,可以让人得到思想启发,树立崇高理想,涵养浩然之气.某初级中学为了解学生近两周平均每天在家阅读时长(单位:小时)的情况,从本校学生中随机抽取了部分学生进行问卷调查,并将结果绘制成如下不完整的频数分布直方图和扇形统计图.
根据以上信息,解答下列问题:
(1)、在这次抽样调查中,共调查了名学生;(2)、请补全频数分布直方图,并计算在扇形统计图中C类所对应扇形的圆心角的度数;(3)、若该校有学生1200人,试估计该校学生近两周平均每天在家阅读时长不足1个小时的人数.22. 如图,正比例函数与反比例函数的图像交于点 , 点是反比例函数图像上的一动点.过点作轴,垂足为 , 交直线于点.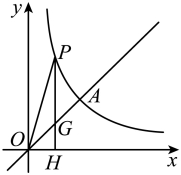 (1)、求与的值;(2)、若的面积是2,求此时点的坐标.23. 为振兴乡村经济,弘扬“四敢”精神,某村拟建 , 两类展位供当地的农产品展览和销售.1个类展位的占地面积比1个类展位的占地面积多4平方米,10个类展位和5个类展位的占地面积共280平方米.建类展位每平方米的费用为120元,建类展位每平方米的费用为100元.(1)、求每个 , 类展位占地面积各为多少平方米;(2)、该村拟建 , 两类展位共40个,且类展位的数量不大于类展位数量的2倍,求建造这40个展位的最小费用.24. 如图,已知是的直径,点 , 点均在上,连接交于点 , , .
(1)、求与的值;(2)、若的面积是2,求此时点的坐标.23. 为振兴乡村经济,弘扬“四敢”精神,某村拟建 , 两类展位供当地的农产品展览和销售.1个类展位的占地面积比1个类展位的占地面积多4平方米,10个类展位和5个类展位的占地面积共280平方米.建类展位每平方米的费用为120元,建类展位每平方米的费用为100元.(1)、求每个 , 类展位占地面积各为多少平方米;(2)、该村拟建 , 两类展位共40个,且类展位的数量不大于类展位数量的2倍,求建造这40个展位的最小费用.24. 如图,已知是的直径,点 , 点均在上,连接交于点 , , . (1)、若 , 求的长;(2)、若记的面积为 , 的面积为 , 求的值.25. 如图,在矩形中, , , 是上一点,.是上的动点,连接 , 是上一点且(为常数,),分别过点 , 作 , 的垂线,交点为.设的长为 , 的长为.
(1)、若 , 求的长;(2)、若记的面积为 , 的面积为 , 求的值.25. 如图,在矩形中, , , 是上一点,.是上的动点,连接 , 是上一点且(为常数,),分别过点 , 作 , 的垂线,交点为.设的长为 , 的长为. (1)、若 , , 则的值是.(2)、若时,求的最大值.(3)、在点从点到点的整个运动过程中,若线段上存在唯一的一点 , 求此时的值.26. 如图,已知抛物线( , , 为常数,)交轴于、两点,交轴于 , 将该抛物线位于直线(为常数,)下方的部分沿直线翻折,其余部分不变,得到的新图像记为“图像”.
(1)、若 , , 则的值是.(2)、若时,求的最大值.(3)、在点从点到点的整个运动过程中,若线段上存在唯一的一点 , 求此时的值.26. 如图,已知抛物线( , , 为常数,)交轴于、两点,交轴于 , 将该抛物线位于直线(为常数,)下方的部分沿直线翻折,其余部分不变,得到的新图像记为“图像”.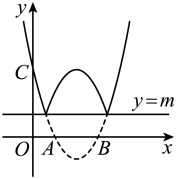 (1)、求该抛物线的解析式;(2)、若时,直线与图像有三个交点,求的值;(3)、若直线与图像有四个交点,直接写出的取值范围.
(1)、求该抛物线的解析式;(2)、若时,直线与图像有三个交点,求的值;(3)、若直线与图像有四个交点,直接写出的取值范围.