江苏省苏州高新区2022-2023学年九年级下学期阳光调研数学试卷(一模)
试卷更新日期:2023-04-06 类型:中考模拟
一、单选题
-
1. 如果温度上升 ,记作 ,那么温度下降 记作( )A、 B、 C、 D、2. 华为手机使用了自主研发的海思麒麟芯片,目前最新的型号是麒麟990.芯片是由很多晶体管组成的,而芯片技术追求是体积更小的晶体管,以便获得更小的芯片和更低的电力功耗,而麒麟990的晶体管栅极的宽度达到了 毫米,将数据 用科学记数法表示为( )A、 B、 C、 D、3. 下列运算中,正确的是( )A、 B、 C、 D、4. 如图,已知 , 直角三角板的直角顶点在直线a上,若 , 则等于( )
 A、 B、 C、 D、5. 如图,在平面直角坐标系中,点A在x轴负半轴上,点 , 连接交y轴于点B.若 , 则的值是( )
A、 B、 C、 D、5. 如图,在平面直角坐标系中,点A在x轴负半轴上,点 , 连接交y轴于点B.若 , 则的值是( ) A、 B、 C、 D、6. 幻方的历史悠久,传说最早出现在夏禹时代的“洛书”(如图1),把洛书用今天的数学符号翻译出来,就是一个三阶幻方(如图2),其每行、每列及每条对角线上的三个格子中的数字之和都等于15.图3也是一个三阶幻方,其每行、每列及每条对角线上的三个格子中的数字之和都等于s,则此三阶幻方中s的值为( )
A、 B、 C、 D、6. 幻方的历史悠久,传说最早出现在夏禹时代的“洛书”(如图1),把洛书用今天的数学符号翻译出来,就是一个三阶幻方(如图2),其每行、每列及每条对角线上的三个格子中的数字之和都等于15.图3也是一个三阶幻方,其每行、每列及每条对角线上的三个格子中的数字之和都等于s,则此三阶幻方中s的值为( ) A、34 B、36 C、42 D、437. 已知函数y与自变量x的部分对应值如表:
A、34 B、36 C、42 D、437. 已知函数y与自变量x的部分对应值如表:x
…
2
4
…
y
…
m
n
2
…
对于下列命题:①若y是x的反比例函数,则;②若y是x的一次函数,则;③若y是x的二次函数,则.其中正确的个数是( )
A、0个 B、1个 C、2个 D、3个8. 如图,在中, , .分别以点C,A为圆心,以2和3为半径作弧,两弧交于点D(点D在的左侧),连接 , 则的最大值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 若代数式有意义,则实数x的取值范围是.10. 数据6,7,8,9的中位数是.11. 一个圆锥的母线长是5,底面半径为4,这个圆锥的侧面积为.12. 如图,直线与x轴、y轴分别相交于点A,B两点,将线段绕着点A按顺时针方向旋转 , 点B恰好落在反比例函数在第一象限图象上的点D.则.
 13. 如图.在Rt△ABC中,∠A=90°,AC=4.按以下步骤作图:(1)以点B为圆心,适当长为半径画弧,分别交线段BA,BC于点M,N;(2)以点C为圆心,BM长为半径画弧,交线段CB于点D;(3)以点D为圆心,MN长为半径画弧,与第2步中所面的弧相交于点E;(4)过点E画射线CE,与AB相交于点F.当AF=3时,BC的长是.
13. 如图.在Rt△ABC中,∠A=90°,AC=4.按以下步骤作图:(1)以点B为圆心,适当长为半径画弧,分别交线段BA,BC于点M,N;(2)以点C为圆心,BM长为半径画弧,交线段CB于点D;(3)以点D为圆心,MN长为半径画弧,与第2步中所面的弧相交于点E;(4)过点E画射线CE,与AB相交于点F.当AF=3时,BC的长是.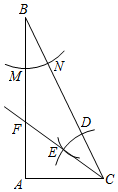 14. 东汉时期的数学家赵爽在注解周髀算经时,给出的“赵爽弦图”是我国古代数学的瑰宝,如图 , 四个直角三角形是全等的,且直角三角形的长直角边与短直角边之比为 , 现连接四条线段得到图的新的图案.若随机向该图形内掷一枚针,则针尖落在图中阴影区域的概率为.
14. 东汉时期的数学家赵爽在注解周髀算经时,给出的“赵爽弦图”是我国古代数学的瑰宝,如图 , 四个直角三角形是全等的,且直角三角形的长直角边与短直角边之比为 , 现连接四条线段得到图的新的图案.若随机向该图形内掷一枚针,则针尖落在图中阴影区域的概率为. 15. 在中学数学中求一些图形面积时,经常用到“同底等高”“等底等高”等数学思想方法,我们称它为等积变换.如图,BD为的对角线,M、N分别在AD、AB上,且 , 若 , 则.
15. 在中学数学中求一些图形面积时,经常用到“同底等高”“等底等高”等数学思想方法,我们称它为等积变换.如图,BD为的对角线,M、N分别在AD、AB上,且 , 若 , 则. 16. 如图,M,N是的边上的两个点(), , , .若边上有且只有1个点P,满足是等腰三角形,则a的取值范围是.
16. 如图,M,N是的边上的两个点(), , , .若边上有且只有1个点P,满足是等腰三角形,则a的取值范围是.
三、解答题
-
17. 计算:18. 解不等式组:19. 已知: , 求代数式的值.20. “双减”政策的实施,不仅减轻了学生的负担,也减轻了家长的负担,回归了教育的初衷.某校计划在某个班向家长展示“双减”背景下的课堂教学活动,用于展开活动的备选班级共5个,其中有2个为八年级班级(分别用A、B表示),3个为九年级班级(分别用C、D、E表示),由于报名参加观摩课堂教学活动的家长较多,学校计划分两周进行,第一周先从这5个备选班级中任意选择一个开展活动,第二周再从剩下的四个备选班级中任意选择一个开展活动.(1)、第一周选择的是八年级班级的概率为;(2)、请用列表法或画树状图的方法求两次选中的既有八年级班级又有九年级班级的概率.21. 如图,矩形中,点E、F分别在边、上,且.
 (1)、求证:;(2)、若 , , 若四边形是菱形,求的长度.22. 设中学生体质健康综合评定成绩为x分,满分为100分,规定:为A级,为B级,为C级,为D级.现随机抽取福海中学部分学生的综合评定成绩,请根据图中的信息,解答下列问题:
(1)、求证:;(2)、若 , , 若四边形是菱形,求的长度.22. 设中学生体质健康综合评定成绩为x分,满分为100分,规定:为A级,为B级,为C级,为D级.现随机抽取福海中学部分学生的综合评定成绩,请根据图中的信息,解答下列问题: (1)、在这次调查中,一共抽取了 名学生, ;(2)、补全条形统计图;(3)、扇形统计图中C级对应的圆心角为 度;(4)、若该校共有2000名学生,请你估计该校D级学生有多少名?23. 在某张航海图上,标明了三个观测点的坐标,如图, , , , 由三个观测点确定的圆形区域是海洋生物保护区.
(1)、在这次调查中,一共抽取了 名学生, ;(2)、补全条形统计图;(3)、扇形统计图中C级对应的圆心角为 度;(4)、若该校共有2000名学生,请你估计该校D级学生有多少名?23. 在某张航海图上,标明了三个观测点的坐标,如图, , , , 由三个观测点确定的圆形区域是海洋生物保护区. (1)、求圆形区域的面积;(2)、某时刻海面上出现渔船A,在观测点O测得A位于北偏东45°,同时在观测点B测得A位于北偏东29°,求观测点B到A船的距离(结果精确到0.1,参考数据: , , ).24. 如图①,在中, , 是外接圆上一点,连接 , 过点作 , 交的延长线于点 , 交于点.
(1)、求圆形区域的面积;(2)、某时刻海面上出现渔船A,在观测点O测得A位于北偏东45°,同时在观测点B测得A位于北偏东29°,求观测点B到A船的距离(结果精确到0.1,参考数据: , , ).24. 如图①,在中, , 是外接圆上一点,连接 , 过点作 , 交的延长线于点 , 交于点. (1)、求证:四边形是平行四边形;(2)、如图②,若为直径, , , 求的长.25. 苏州乐园森林世界位于美丽的大阳山东南角,包含25项森林主题演出与游乐项目,其中“冲上云霄”是其经典项目之一,其轨道总长约1040米,极限高度62.5米.如图所示,为“冲上云霄”过山车的一部分轨道(B为轨道最低点),它可以看成一段抛物线.其中米,米(轨道厚度忽略不计).
(1)、求证:四边形是平行四边形;(2)、如图②,若为直径, , , 求的长.25. 苏州乐园森林世界位于美丽的大阳山东南角,包含25项森林主题演出与游乐项目,其中“冲上云霄”是其经典项目之一,其轨道总长约1040米,极限高度62.5米.如图所示,为“冲上云霄”过山车的一部分轨道(B为轨道最低点),它可以看成一段抛物线.其中米,米(轨道厚度忽略不计). (1)、求抛物线的函数关系式;(2)、在轨道距离地面5米处有两个位置P和C,当过山车运动到C处时,又进入下坡段(接口处轨道忽略不计).已知轨道抛物线的形状与抛物线完全相同,求的长度;(3)、现需要对轨道下坡段进行一种安全加固,建造某种材料的水平和竖直支架、、、 , 且要求.如何设计支架,才能用料最少?最少需要材料多少米?26.(1)、如图①,在正方形中,E,F分别是 , 边上的动点,且 , 将绕点D逆时针旋转90°,得到 , 可以证明 , 进一步推出 , , 之间的数量关系为;
(1)、求抛物线的函数关系式;(2)、在轨道距离地面5米处有两个位置P和C,当过山车运动到C处时,又进入下坡段(接口处轨道忽略不计).已知轨道抛物线的形状与抛物线完全相同,求的长度;(3)、现需要对轨道下坡段进行一种安全加固,建造某种材料的水平和竖直支架、、、 , 且要求.如何设计支架,才能用料最少?最少需要材料多少米?26.(1)、如图①,在正方形中,E,F分别是 , 边上的动点,且 , 将绕点D逆时针旋转90°,得到 , 可以证明 , 进一步推出 , , 之间的数量关系为;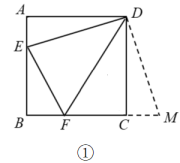 (2)、在图①中,连接分别交和于P,Q两点, 求证:;(3)、如图②,在菱形中, , 点E,F分别是边 , 上的动点(不与端点重合),且 , 连接分别与边 , 交于M,N.当时,猜想 , , 之间存在什么样的数量关系,并证明你的结论.
(2)、在图①中,连接分别交和于P,Q两点, 求证:;(3)、如图②,在菱形中, , 点E,F分别是边 , 上的动点(不与端点重合),且 , 连接分别与边 , 交于M,N.当时,猜想 , , 之间存在什么样的数量关系,并证明你的结论.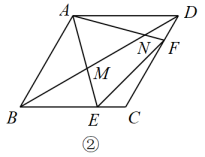 27. 平面直角坐标系中,反比例函数的图象与一次函数图象交于A、B两点(点A在点B左侧).(1)、求A、B两点的坐标(用含k的代数式表示);(2)、当时,过y轴正半轴上一动点作平行于x轴的直线,分别与一次函数、反比例函数的图象相交于D、E两点,若 , 求n的值;(3)、若一次函数图象与x轴交于点F, , 直接写出k的取值范围.
27. 平面直角坐标系中,反比例函数的图象与一次函数图象交于A、B两点(点A在点B左侧).(1)、求A、B两点的坐标(用含k的代数式表示);(2)、当时,过y轴正半轴上一动点作平行于x轴的直线,分别与一次函数、反比例函数的图象相交于D、E两点,若 , 求n的值;(3)、若一次函数图象与x轴交于点F, , 直接写出k的取值范围.