湖南省株洲市2023年初中毕业考试模拟试卷数学试题(一)
试卷更新日期:2023-04-06 类型:中考模拟
一、单选题
-
1. 在﹣1,﹣2,0,1四个数中最小的数是( )A、-1 B、-2 C、0 D、12. 为了方便市民出行,提倡低碳交通,近几年我市大力发展公共自行车系统,根据规划,市公共自行车总量明年将达辆,用科学记数法表示是( )A、 B、 C、 D、3. 计算(a2b)3的结果是( )A、a6b3 B、a2b3 C、a5b3 D、a6b4. 下列图案中,既是中心对称图形也是轴对称图形的个数为( )
 A、1个 B、2个 C、3个 D、4个5. 已知一个多边形的内角和为1080°,则这个多边形是( )A、九边形 B、八边形 C、七边形 D、六边形6. 已知不等式组 ,其解集在数轴上表示正确的是( )A、
A、1个 B、2个 C、3个 D、4个5. 已知一个多边形的内角和为1080°,则这个多边形是( )A、九边形 B、八边形 C、七边形 D、六边形6. 已知不等式组 ,其解集在数轴上表示正确的是( )A、 B、
B、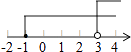 C、
C、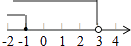 D、
D、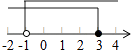 7. 为了了解某班同学一周的课外阅读量,任选班上15名同学进行调查,统计如表,则下列说法错误的是( )
7. 为了了解某班同学一周的课外阅读量,任选班上15名同学进行调查,统计如表,则下列说法错误的是( )阅读量(单位:本/周)
0
1
2
3
4
人数(单位:人)
1
4
6
2
2
A、中位数是2 B、平均数是2 C、众数是2 D、极差是28. 已知一元二次方程 的两个实数根分别是 x1 、 x2 则 x12 x2 + x1 x22 的值为( )A、-6 B、- 3 C、3 D、69. 如图,将斜边长为4的直角三角板放在直角坐标系中,两条直角边分别与坐标轴重合,P为斜边的中点.现将此三角板绕点O顺时针旋转后点P的对应点Q的坐标是( ) A、 B、 C、 D、10. 如图,二次函数图象的顶点为 , 其图象与轴的交点、的横坐标分别为和 , 则下列结论中:(1) , (2) , (3) , (4)当时,是等腰直角三角形,正确的个数是( )
A、 B、 C、 D、10. 如图,二次函数图象的顶点为 , 其图象与轴的交点、的横坐标分别为和 , 则下列结论中:(1) , (2) , (3) , (4)当时,是等腰直角三角形,正确的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 在函数 中,自变量x的取值范围是 .12. 因式分解:.13. 用2,3,4三个数字排成一个三位数,则排出的数是偶数的概率为 .
14. 在平面直角坐标系xOy中,点P(2,a)在正比例函数 的图象上,则点Q(a,3a﹣5)位于第象限.15.如图,直线AB,CD被直线AE所截,AB∥CD,∠A=110°,则∠1=度.
 16. 如图,四边形ABCD内接于⊙O,已知∠ADC=140°,则∠AOC=.
16. 如图,四边形ABCD内接于⊙O,已知∠ADC=140°,则∠AOC=. 17. 以正方形ABCD两条对角线的交点O为坐标原点,建立如图所示的平面直角坐标系,双曲线y= 经过点D,则正方形ABCD的面积是 .
17. 以正方形ABCD两条对角线的交点O为坐标原点,建立如图所示的平面直角坐标系,双曲线y= 经过点D,则正方形ABCD的面积是 .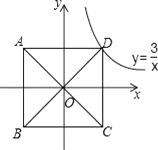 18. 有一个正六面体骰子,放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动90°算一次,则滚动第2017次后,骰子朝下一面的点数是.
18. 有一个正六面体骰子,放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动90°算一次,则滚动第2017次后,骰子朝下一面的点数是.
三、解答题
-
19. 计算:20. 先化简,再求值: , 其中满足.21. 某校在开展读书交流活动中,全体师生积极捐书,为了解所捐书籍的种类,对部分书籍进行了抽样调查,李老师根据调查数据绘制了如下不完整的统计图.请你根据统计回答下面问题:
 (1)、本次抽样调查的书籍有多少本?(2)、请补全条形统计图;(3)、求出图1中表示文学类书籍的扇形圆心角度数;(4)、本次活动师生共捐书1200本,请估计有多少本科普类图书?22. 如图,点E是正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.
(1)、本次抽样调查的书籍有多少本?(2)、请补全条形统计图;(3)、求出图1中表示文学类书籍的扇形圆心角度数;(4)、本次活动师生共捐书1200本,请估计有多少本科普类图书?22. 如图,点E是正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF. (1)、求证:△ABF≌△CBE;(2)、判断△CEF的形状,并说明理由.23. 随着生活质量的提高,人们健康意识逐渐增强,安装净水设备的百姓家庭越来越多.某厂家从去年开始投入生产净水器,生产净水器的总量(台)与今年的生产天数(天)的关系如图所示.今年生产90天后,厂家改进了技术,平均每天的生产数量达到30台.
(1)、求证:△ABF≌△CBE;(2)、判断△CEF的形状,并说明理由.23. 随着生活质量的提高,人们健康意识逐渐增强,安装净水设备的百姓家庭越来越多.某厂家从去年开始投入生产净水器,生产净水器的总量(台)与今年的生产天数(天)的关系如图所示.今年生产90天后,厂家改进了技术,平均每天的生产数量达到30台. (1)、求与之间的函数表达式;(2)、如果厂家制定总量不少于6000台的生产计划,那么在改进技术后,至少还要多少天完成生产计划?24. 如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
(1)、求与之间的函数表达式;(2)、如果厂家制定总量不少于6000台的生产计划,那么在改进技术后,至少还要多少天完成生产计划?24. 如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.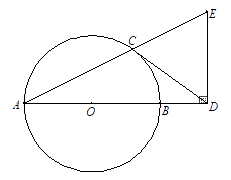 (1)、求证:DC=DE;(2)、若tan∠CAB= ,AB=3,求BD的长.
(1)、求证:DC=DE;(2)、若tan∠CAB= ,AB=3,求BD的长.
25. 阅读下面材料: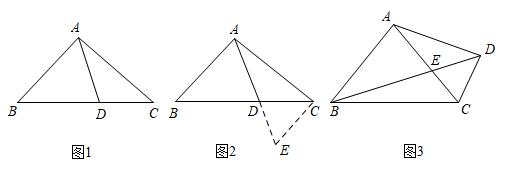
小腾遇到这样一个问题:如图1,在△ABC中,点D在线段BC上,∠BAD=75°,∠CAD=30°,AD=2,BD=2DC,求AC的长.
小腾发现,过点C作CE∥AB,交AD的延长线于点E,经过推理和计算能够使问题得到解决,如图2.
(1)、请回答:∠ACE的度数为 , AC的长为.(2)、参考小腾思考问题的方法,解决问题:如图3,在四边形ABCD中,∠BAC=90°,∠CAD=30°,∠ADC=75°,AC与BD交于点E,AE=2,BE=2ED,求BC的长.
26. 如图1,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(4,0)两点,与y轴相交于点C,连结BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.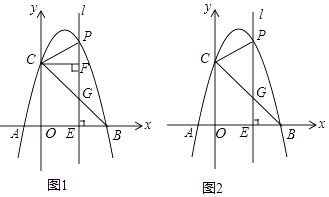 (1)、求抛物线的表达式;(2)、当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;(3)、如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由.
(1)、求抛物线的表达式;(2)、当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;(3)、如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由.