河南省新乡市封丘县2023年九年级中考第一次调研模拟数学试题
试卷更新日期:2023-04-06 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 据了解,北京冬奥会运动场馆的温度最低可达零下30多摄氏度,为了让颁奖礼仪服装美观又保暖,衣服里特意添加了一片片黑色的材料,这是中国航发为本届冬奥会研发的石墨烯发热材料,可以快速升温.研究证实,石墨烯中碳原子的配位数为3,每两个相邻碳原子间的键长为0.000000000142米,键与键之间的夹角为120°,将0.000000000142用科学记数法表示为( )A、 B、 C、 D、3. 如图,是由5个大小相同的小正方体搭成的几何体,它的左视图是( )
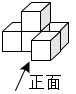 A、
A、 B、
B、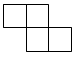 C、
C、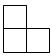 D、
D、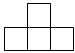 4. 如图,已知a∥b,含30°角的直角三角板的顶点在直线b上,若∠1=24°,则∠2等于( )
4. 如图,已知a∥b,含30°角的直角三角板的顶点在直线b上,若∠1=24°,则∠2等于( ) A、110° B、112° C、114° D、120°5. 下列运算正确的是( )A、-3x4+2x4=5x4 B、x6÷x2=x3 C、-5(x4)2=-5x8 D、(x+2)2=x2+46. 下列说法正确的是( )A、为了解春节期间河南省的空气质量,采用全面调查 B、射击运动员射击一次,命中靶心为必然事件 C、数据2,2,2,2,2的方差为0 D、数据6,8,6,13,8,12的众数为87. 方程的根的情况是( )A、有两个不相等的实数根 B、有一个实数根 C、有两个相等的实数根 D、没有实数根8. 如图,在矩形ABCD中,AB=8,BC=6,以B为圆心,适当的长为半径画弧,交BD,BC于M,N两点;再分别以M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线BP交CD于点F;再以B为圆心,BD的长为半径画弧,交射线BP于点E,则EF的长为( )
A、110° B、112° C、114° D、120°5. 下列运算正确的是( )A、-3x4+2x4=5x4 B、x6÷x2=x3 C、-5(x4)2=-5x8 D、(x+2)2=x2+46. 下列说法正确的是( )A、为了解春节期间河南省的空气质量,采用全面调查 B、射击运动员射击一次,命中靶心为必然事件 C、数据2,2,2,2,2的方差为0 D、数据6,8,6,13,8,12的众数为87. 方程的根的情况是( )A、有两个不相等的实数根 B、有一个实数根 C、有两个相等的实数根 D、没有实数根8. 如图,在矩形ABCD中,AB=8,BC=6,以B为圆心,适当的长为半径画弧,交BD,BC于M,N两点;再分别以M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线BP交CD于点F;再以B为圆心,BD的长为半径画弧,交射线BP于点E,则EF的长为( ) A、 B、 C、 D、9. 将含有角的直角三角板按如图所示的方式放置在平面直角坐标系中,在轴上,若 , 将角板绕原点O逆时针旋转,每秒旋转 , 则第2019秒时,点A的对应点的坐标为( )
A、 B、 C、 D、9. 将含有角的直角三角板按如图所示的方式放置在平面直角坐标系中,在轴上,若 , 将角板绕原点O逆时针旋转,每秒旋转 , 则第2019秒时,点A的对应点的坐标为( ) A、 B、 C、 D、10. 如图,在矩形ABCD中,AD=8 cm,AB=6 cm.动点E从点C开始沿边CB向终点B以2 cm/s的速度运动,同时动点F从点C出发沿边CD向点D以1 cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是( )
A、 B、 C、 D、10. 如图,在矩形ABCD中,AD=8 cm,AB=6 cm.动点E从点C开始沿边CB向终点B以2 cm/s的速度运动,同时动点F从点C出发沿边CD向点D以1 cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是( )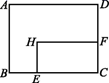 A、
A、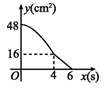 B、
B、 C、
C、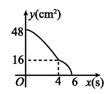 D、
D、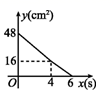
二、填空题
-
11. 若有意义,则实数x的取值范围是.12. 不等式的解集为.13. 如图,管中放置着三根同样的绳子AA1、BB1、CC1 . 小明在左侧选两个打一个结,小红在右侧选两个打一个结,则这三根绳子能连结成一根长绳的概率为 .
 14. 如图,在菱形中, , , 扇形的半径为6,圆心角为 , 则阴影部分的面积是.
14. 如图,在菱形中, , , 扇形的半径为6,圆心角为 , 则阴影部分的面积是. 15. 如图所示,正方形纸片的边长为4.点E为边上不与端点重合的一动点,将纸片沿过的直线折叠,点A的落点记为F,连接、 , 若是以为腰的等腰三角形,则.
15. 如图所示,正方形纸片的边长为4.点E为边上不与端点重合的一动点,将纸片沿过的直线折叠,点A的落点记为F,连接、 , 若是以为腰的等腰三角形,则.
三、解答题
-
16. 计算:(1)、(2)、17. 年月,教育部印发关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见 , 明确要求初中生课外作业完成时间不超过分钟.为了了解学生每天完成课外作业时间,某校数学兴趣小组决定对本校学生每天完成课外作业所用时间进行调查,他们随机抽取本校部分学生进行了问卷调查,并将调查结果分为 , , , 四个等级,列表如下:
等级
每天完成课外作业时间分钟
根据调查结果绘制了如图所示的两幅不完整的统计图,请你根据图中信息解答下列问题:
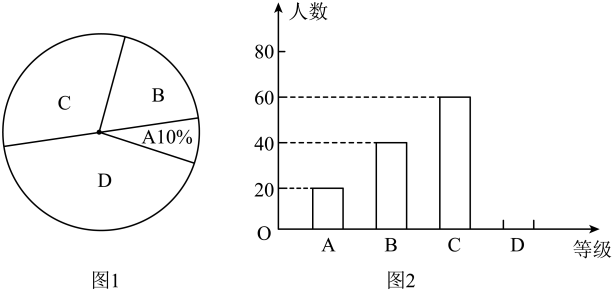 (1)、本次抽样调查共抽取了多少名学生?将条形统计图补充完整.(2)、学生每天完成课外作业时间的中位数落在等级.(3)、请对该校学生每天完成课外作业时间作出评价,并提出两条合理化建议.18. 一次函数的图象与反比例函数的图象相交于 , 两点.
(1)、本次抽样调查共抽取了多少名学生?将条形统计图补充完整.(2)、学生每天完成课外作业时间的中位数落在等级.(3)、请对该校学生每天完成课外作业时间作出评价,并提出两条合理化建议.18. 一次函数的图象与反比例函数的图象相交于 , 两点.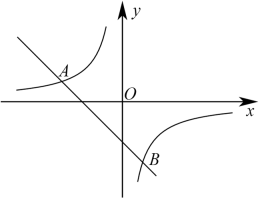 (1)、求这个反比例函数的解析式;(2)、根据图象写出使一次函数值不大于反比例函数值的x的取值范围.(3)、若动点E在y轴上,且 , 求动点E的坐标.19. 某校组织学生到黄河某段流域进行研学旅行.某兴趣小组在只有米尺和测角仪的情况下,想要求出河南段黄河某处的宽度(不能到对岸)如图,已知该段河对岸岸边有一点A,兴趣小组以A为参照点在河这边沿河边任取两点B,C,测得 , , 量得BC的长为.求河的宽度.(结果精确到 , 参考数据 , , )20. 某实验中学计划购买甲、乙两种树苗绿化校园.已知用720元购买甲种树苗的棵数比用672元购买乙种树苗的棵数少5棵,且乙种树苗的单价为甲种树苗单价的.(1)、问甲、乙两种树苗的单价分别为多少元?(2)、学校计划购买甲、乙两种树苗共120棵,并且要求乙种树苗的数量不多于甲种树苗数量的 , 那么应按照什么方案购买才能使费用最少,最少费用应为多少?21. 在平面直角坐标系中,已知抛物线.(1)、抛物线的对称轴是直线;(2)、若抛物线的顶点在x轴上,求该抛物线的解析式;(3)、若 , 对于抛物线上的两点 , 当 , 时,均满足 , 求t的取值范围是多少?22. 如图,已知 , 圆心O在上点M与点C分别是与的交点,点D是与的交点,点P是延长线与的交点,且.
(1)、求这个反比例函数的解析式;(2)、根据图象写出使一次函数值不大于反比例函数值的x的取值范围.(3)、若动点E在y轴上,且 , 求动点E的坐标.19. 某校组织学生到黄河某段流域进行研学旅行.某兴趣小组在只有米尺和测角仪的情况下,想要求出河南段黄河某处的宽度(不能到对岸)如图,已知该段河对岸岸边有一点A,兴趣小组以A为参照点在河这边沿河边任取两点B,C,测得 , , 量得BC的长为.求河的宽度.(结果精确到 , 参考数据 , , )20. 某实验中学计划购买甲、乙两种树苗绿化校园.已知用720元购买甲种树苗的棵数比用672元购买乙种树苗的棵数少5棵,且乙种树苗的单价为甲种树苗单价的.(1)、问甲、乙两种树苗的单价分别为多少元?(2)、学校计划购买甲、乙两种树苗共120棵,并且要求乙种树苗的数量不多于甲种树苗数量的 , 那么应按照什么方案购买才能使费用最少,最少费用应为多少?21. 在平面直角坐标系中,已知抛物线.(1)、抛物线的对称轴是直线;(2)、若抛物线的顶点在x轴上,求该抛物线的解析式;(3)、若 , 对于抛物线上的两点 , 当 , 时,均满足 , 求t的取值范围是多少?22. 如图,已知 , 圆心O在上点M与点C分别是与的交点,点D是与的交点,点P是延长线与的交点,且. (1)、求证:是的切线:(2)、若 , , 求的值.23. 在四边形中ABCD,点E为AB边上的一点,点F为对角线BD上的一点,且EF⊥AB.
(1)、求证:是的切线:(2)、若 , , 求的值.23. 在四边形中ABCD,点E为AB边上的一点,点F为对角线BD上的一点,且EF⊥AB.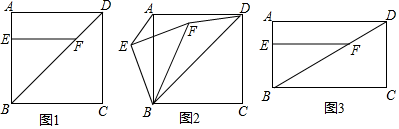 (1)、若四边形ABCD为正方形.
(1)、若四边形ABCD为正方形.①如图1,请直接写出AE与DF的数量关系;
②将△EBF绕点B逆时针旋转到图2所示的位置,连接AE,DF,猜想AE与DF的数量关系并说明理由;
(2)、如图3,若四边形ABCD为矩形,BC=mAB,其它条件都不变,将△EBF绕点B顺时针旋转α(0°<α<90°)得到△E′BF′,连接AE′,DF′,请在图3中画出草图,并直接写出AE′与DF′的数量关系.