河南省洛阳市伊滨区2022-2023学年九年级上学期第二次质检数学试题
试卷更新日期:2023-04-06 类型:中考模拟
一、单选题
-
1. 下列图形既是中心对称图形也是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 抛物线的函数表达式为 ,若将 轴向上平移2个单位长度,将 轴向左平移3个单位长度,则该抛物线在新的平面直角坐标系中的函数表达式为( )A、 B、 C、 D、3. 将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )
2. 抛物线的函数表达式为 ,若将 轴向上平移2个单位长度,将 轴向左平移3个单位长度,则该抛物线在新的平面直角坐标系中的函数表达式为( )A、 B、 C、 D、3. 将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )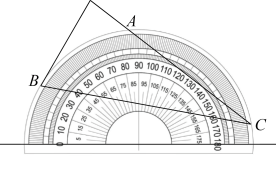 A、28° B、30° C、36° D、56°4. 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=25°,则∠BAA′的度数是( )
A、28° B、30° C、36° D、56°4. 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=25°,则∠BAA′的度数是( ) A、55° B、60° C、65° D、70°5. 已知(0,y1),( ,y2),(3,y3)是抛物线y=ax2﹣4ax+1(a是常数,且a<0)上的点,则( )A、y1>y2>y3 B、y3>y2>y1 C、y2>y3>y1 D、y2>y1>y36. 若点O是 的外心,且∠BOC=50°,则∠BAC的度数为( )A、25° B、130° C、25°或130° D、25°或155°7. 如图,已知BC是⊙O的直径,半径OA⊥BC,点D在劣弧AC上(不与点A,点C重合),BD与OA交于点E.设∠AED=α,∠AOD=β,则( )
A、55° B、60° C、65° D、70°5. 已知(0,y1),( ,y2),(3,y3)是抛物线y=ax2﹣4ax+1(a是常数,且a<0)上的点,则( )A、y1>y2>y3 B、y3>y2>y1 C、y2>y3>y1 D、y2>y1>y36. 若点O是 的外心,且∠BOC=50°,则∠BAC的度数为( )A、25° B、130° C、25°或130° D、25°或155°7. 如图,已知BC是⊙O的直径,半径OA⊥BC,点D在劣弧AC上(不与点A,点C重合),BD与OA交于点E.设∠AED=α,∠AOD=β,则( )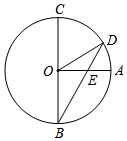 A、3α+β=180° B、2α+β=180° C、3α﹣β=90° D、2α﹣β=90°8. 已知二次函数 ( 为常数)的图象与x轴有交点,且当 时,y随x的增大而增大,则a的取值范围是( )A、 B、 C、 D、9. 如图,在 中,顶点 , , ,将 与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转 ,则第70次旋转结束时,点D的坐标为( )
A、3α+β=180° B、2α+β=180° C、3α﹣β=90° D、2α﹣β=90°8. 已知二次函数 ( 为常数)的图象与x轴有交点,且当 时,y随x的增大而增大,则a的取值范围是( )A、 B、 C、 D、9. 如图,在 中,顶点 , , ,将 与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转 ,则第70次旋转结束时,点D的坐标为( ) A、 B、 C、 ) D、10. 如图,O是正内一点, , , , 将线段BO以点B为旋转中心逆时针旋转得到线段 , 下列结论:
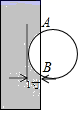
A、 B、 C、 ) D、10. 如图,O是正内一点, , , , 将线段BO以点B为旋转中心逆时针旋转得到线段 , 下列结论:

可以由绕点B逆时针旋转得到;
点O与的距离为4;
;
;
其中正确的结论是
A、 B、 C、 D、二、填空题
-
11. 在直角坐标系中,将点关于原点的对称点向左平移个单位长度得到的点的坐标是.12. 《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为1寸,锯道 尺(1尺=10寸),则该圆材的直径为寸.
 13. 如图,圆锥的侧面展开图是一个圆心角为120°的扇形,若圆锥的底面圆半径是 ,则圆锥的母线l= .
13. 如图,圆锥的侧面展开图是一个圆心角为120°的扇形,若圆锥的底面圆半径是 ,则圆锥的母线l= . 14. 如图所示的网格中,每个小正方形的边长均为1,点A,B,D均在小正方形的顶点上,且点B,C在上, , 则的长为.
14. 如图所示的网格中,每个小正方形的边长均为1,点A,B,D均在小正方形的顶点上,且点B,C在上, , 则的长为. 15. 如图,在中, , , 点为的中点,点在上,且 , 将绕点在平面内旋转,点的对应点为点 , 连接 , 当时,的长为 .
15. 如图,在中, , , 点为的中点,点在上,且 , 将绕点在平面内旋转,点的对应点为点 , 连接 , 当时,的长为 .
三、解答题
-
16. 解方程:(1)、3x2-5x+2=0(2)、(x+1)(x+3)=817. 如图,的顶点坐标分别为 , , .

⑴画出关于点的中心对称图形;
⑵画出绕点逆时针旋转90°的;直接写出点的坐标为 ▲ ;
⑶在(2)的条件下,求出线段所扫过图形的面积.18. 已知:如图,ABC为锐角三角形,AB=AC,CD∥AB.
求作:线段BP,使得点P在直线CD上,且∠ABP= .
作法:①以点A为圆心,AC长为半径画圆,交直线CD于C,P两点;②连接BP.线段BP就是所求作线段.
(1)、使用直尺和圆规,依作法补全图形(保留作图痕迹)(2)、完成下面的证明.证明:∵CD∥AB,
∴∠ABP= ▲ .
∵AB=AC,
∴点B在⊙A上.
又∵∠BPC=∠BAC( )(填推理依据)
∴∠ABP=∠BAC
19. 如图,在 中, .以AB为直径的 与线段BC交于点D,过点D作 ,垂足为E,ED的延长线与AB的延长线交于点P. (1)、求证:直线PE是 的切线;(2)、若 的半径为6, ,求CE的长.20. 如图所示,点P是正方形ABCD内的一点,连接AP,BP,CP,将△PAB绕着点B顺时针旋转90°到△P′CB的位置.若AP=2,BP=4,∠APB=135°,求PP′及PC的长.
(1)、求证:直线PE是 的切线;(2)、若 的半径为6, ,求CE的长.20. 如图所示,点P是正方形ABCD内的一点,连接AP,BP,CP,将△PAB绕着点B顺时针旋转90°到△P′CB的位置.若AP=2,BP=4,∠APB=135°,求PP′及PC的长.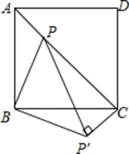 21. 丹东是我国的边境城市,拥有丰富的旅游资源.某景区研发一款纪念品,每件成本为30元,投放景区内进行销售,规定销售单价不低于成本且不高于54元,销售一段时间调研发现,每天的销售数量y(件)与销售单价x(元/件)满足一次函数关系,部分数据如下表所示:
21. 丹东是我国的边境城市,拥有丰富的旅游资源.某景区研发一款纪念品,每件成本为30元,投放景区内进行销售,规定销售单价不低于成本且不高于54元,销售一段时间调研发现,每天的销售数量y(件)与销售单价x(元/件)满足一次函数关系,部分数据如下表所示:销售单价x(元/件)
…
35
40
45
…
每天销售数量y(件)
…
90
80
70
…
(1)、直接写出y与x的函数关系式;(2)、若每天销售所得利润为1200元,那么销售单价应定为多少元?(3)、当销售单价为多少元时,每天获利最大?最大利润是多少元?22. 如图1,在中, , , 点D、E分别在边AB,上, , 连接DC,点M,P,N分别为DE,DC,BC的中点. (1)、观察猜想:图中,线段PM与PN的数量关系是 , 位置关系是;(2)、探究证明:把绕点A逆时针方向旋转到图2的位置,连接 , , , 判断的形状,并说明理由;
(1)、观察猜想:图中,线段PM与PN的数量关系是 , 位置关系是;(2)、探究证明:把绕点A逆时针方向旋转到图2的位置,连接 , , , 判断的形状,并说明理由; (3)、拓展延伸:把绕点A在平面内自由旋转,若 , , 请直接写出面积的最大值.23. 在平面直角坐标系中,二次函数 y=ax2+bx+2 的图象与 x 轴交于 A(﹣3,0),B(1,0)两点,与 y 轴交于点C.
(3)、拓展延伸:把绕点A在平面内自由旋转,若 , , 请直接写出面积的最大值.23. 在平面直角坐标系中,二次函数 y=ax2+bx+2 的图象与 x 轴交于 A(﹣3,0),B(1,0)两点,与 y 轴交于点C. (1)、求这个二次函数的关系解析式 ,x 满足什么值时 y﹤0 ?(2)、点 p 是直线 AC 上方的抛物线上一动点,是否存在点 P , 使△ACP 面积最大?若存在,求出点 P的坐标;若不存在,说明理由(3)、点 M 为抛物线上一动点,在 x 轴上是否存在点 Q , 使以 A、C、M、Q 为顶点的四边形是平行四边形?若存在,直接写出点 Q 的坐标;若不存在,说明理由.
(1)、求这个二次函数的关系解析式 ,x 满足什么值时 y﹤0 ?(2)、点 p 是直线 AC 上方的抛物线上一动点,是否存在点 P , 使△ACP 面积最大?若存在,求出点 P的坐标;若不存在,说明理由(3)、点 M 为抛物线上一动点,在 x 轴上是否存在点 Q , 使以 A、C、M、Q 为顶点的四边形是平行四边形?若存在,直接写出点 Q 的坐标;若不存在,说明理由.