河南省焦作市沁阳市2023届九年级上学期第一次质量检测数学试题

试卷更新日期：2023-04-06 类型：中考模拟

进入出卷网下载

一、单选题

1. 2022年12月4日，神舟十四号载人飞船圆满完成全部既定任务，顺利返回地球家园.六个月的飞天之旅展现了中国航天科技的新高度.下列航天图标，其文字上方的图案是中心对称图形的是（）

A、中国探火 B、
中国行星探测 C、
中国火箭 D、航天神舟

查看试题解析
2. 下列事件中，正确的是（）

A、事件发生的可能性越大，概率越接近1 B、某种彩票中奖的概率是 $\frac{1}{100}$ ，买100张该种彩票一定能中奖 C、抛掷一枚图钉，“针尖朝上”的概率是 $\frac{1}{2}$ D、射击运动员射击一次，命中靶心是必然事件

查看试题解析
3. 关于x的一元二次方程 $x^{2} + (2 a - 3) x + a^{2} - 1 = 0$ 有两个实数根，则a的最大整数解为（）

A、1 B、 $- 1$ C、 $- 2$ D、0

查看试题解析
4. 如图， $Δ A B C$ 内接圆 $⊙ O ， A D$ 是 $⊙ O$ 的直径，若 $∠ B = 25 °$ ，则 $∠ C A D$ 的度数是（）

A、 $60 °$ B、 $65 °$ C、 $70 °$ D、 $75 °$

查看试题解析
5. 已知二次函数y=x²−2x−3的自变量x₁ ， x₂ ， x₃对应的函数值分别为y₁ ， y₂ ， y₃.当−1<x₁<0，1<x₂<2，x₃>3时，y₁ ， y₂ ， y₃三者之间的大小关系是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{2} < y_{1} < y_{3}$ C、 $y_{3} < y_{1} < y_{2}$ D、 $y_{2} < y_{3} < y_{1}$

查看试题解析
6. 在平面直角坐标系中，点 $(a - 3 ， 4)$ 关于原点的对称点为 $(5 ， - b)$ ，则 $a b$ 的值为（）

A、 $- 8$ B、8 C、6 D、 $- 12$

查看试题解析
7. 一个三角形的一边长为12，另外两边长是一元二次方程 $x^{2} - 18 x + 65 = 0$ 的两根，则这个三角形外接圆的半径是（）

A、 $\frac{60}{13}$ B、5 C、 $6.5$ D、8

查看试题解析
8. 某热门电影上映的第一天票房约为2亿元，第二天、第三天持续增长，三天累计票房6.62亿元，若第二天、第三天按相同的增长率增长，则平均每天票房的增长率为（）

A、 $5 %$ B、 $10 %$ C、 $15 %$ D、 $20 %$

查看试题解析
9. 如图， $Δ O A B$ 中， $∠ A O B = 60 ° ， O A = 4$ ，点B的坐标为 $(6 ， 0)$ ，将 $Δ O A B$ 绕点A逆时针旋转得到 $Δ C A D$ ，当点O的对应点C落在 $O B$ 上时，点D的坐标为（）

A、 $(5 \sqrt{3} ， 5 \sqrt{3})$ B、 $(5 \sqrt{3} ， 5)$ C、 $(7 ， 5)$ D、 $(7 ， 3 \sqrt{3})$

查看试题解析
10. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，有下列6个结论：① $a b c > 0$ ；② $b^{2} > 4 a c$ ；③ $2 c < 3 b$ ；④ $a + b > m (a m + b)$ ；⑤方程 $| a x^{2} + b x + c | = m$ 有两个相等的实数根.其中正确的结论有（）

A、①③⑤ B、②③④ C、①④⑤ D、②④⑤

查看试题解析

二、填空题

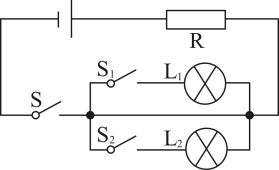
11. 请任意写出一个图象开口向上，且顶点坐标为 $(3 ， - 2)$ 的二次函数解析式.

查看试题解析
12. 在物理实验课上，同学们用三个开关、两个灯泡、一个电源、一个电阻及若干条导线连接如图所示的电路图，随机闭合图中的两个开关，有一个灯泡发光的概率是.

查看试题解析
13. 为落实国家《关于全面加强新时代大中小学劳动教育的意见》，某校准备在校园里利用围墙（墙长 $9 m$ ）和 $21 m$ 长的篱笆墙，围成I区、II区两块矩形劳动实践基地（如图所示）.要使围成的两块矩形总种植面积最大，则 $B C$ 应设计为m.

查看试题解析
14. 如图，扇形 $O A B$ 的圆心角 $∠ A O B = 60 °$ ，将扇形 $O A B$ 沿射线 $A O$ 平移得到扇形 $O ´ A ´ B ´$ ，弧 $A ´ B ´ 与 O B$ 交于点C.若 $O A = 2 \sqrt{3} ， O' O = 2$ ，则阴影部分的面积为.

查看试题解析
15. 如图，在等边三角形 $A B C$ 中， $A B = 2 \sqrt{3}$ ，点D为 $A C$ 的中点，点P在 $A B$ 上，且 $B P = 1$ ，将 $B P$ 绕点B在平面内旋转，点P的对应点为点Q，连接 $A Q ， D Q$ .当 $∠ A D Q = 90 °$ 时， $A Q$ 的长为.

查看试题解析

三、解答题

16. 解方程：

(1)、 $2 x^{2} + 4 = 7 x$ ；

(2)、 $2 {(2 x - 3)}^{2} = 4 x - 6$

查看试题解析
17. 如图，在平面直角坐标系中，已知 $△ A B C$ 的三个顶点的坐标分别为 $A (- 1 ， 1) ， B (- 2 ， 2) ， C (- 4 ， 0)$ ，将 $△ A B C$ 绕原点O顺时针旋转 $90 °$ 后得到 $△ A_{1} B_{1} C_{1}$ .
（ 1 ）作出 $△ A_{1} B_{1} C_{1}$ ，并写出 $A_{1} 、 B_{1} 、 C_{1}$ 三点的坐标： $A_{1}$ ▲ ， $B_{1}$ ▲ ， $C_{1}$ ▲ ；
（ 2 ）求点B旋转到点 $B_{1}$ 的弧长.
（ 3 ）作 $△ A_{1} B_{1} C_{1}$ 于原点对称的图形 $△ A_{2} B_{2} C_{2}$ .

查看试题解析
18. 已知关于x的一元二次方程 $(m - 2) x^{2} - 4 x + 1 = 0$ 有两个实数根 $x_{1} ， x_{2}$ .

(1)、求m的取值范围；

(2)、若 $x_{1} = - 1$ ，求m的值及 $x_{2}$ .

查看试题解析
19. 中华文化源远流长，中华诗词寓意深广，为了弘扬优秀传统文化，某校团委组织了一次诗词大赛，八（1）班准备从甲、乙两名女生和丙、丁两名男生中任选2人代表班级参加比赛.

(1)、如果已经确定女生甲参加比赛，再从其余的候选人中随机选取一人，则男生丙被选中的概率是；

(2)、求所选代表恰好为一名男生和一名女生的概率.（请用“画树状图”或“列表”等方法写出分析过程）

查看试题解析
20. 同学们在操场玩跳大绳游戏，跳大绳时，绳甩到最高处时的形状是抛物线，正在甩绳的甲、乙两名同学拿绳的手间距 $A B$ 为6米，到地面的距离 $A O$ 与 $B D$ 均为0.9米，绳子甩到最高点C处时，最高点距地面的垂直距离为1.8米，距甲同学的水平距离为3米，以点O为原点建立如图所示的平面直角坐标系.

(1)、求该抛物线的解析式；

(2)、如果身高为1.7米的聪聪站在 $O D$ 之间，当绳子甩到最高处时，求聪聪站在距点O的水平距离为多少时，绳子刚好通过他的头顶上方？

查看试题解析
21. 中国5A级旅游景区开封市清明上河园中水车园的水车由立式水轮、竹筒、支撑架、水槽等部件组成，如图是水车园中半径为5m的水车灌田的简化示意图，立式水轮 $⊙ O$ 在水流的作用下利用竹筒将水运送到点A处，水沿水槽 $A P$ 流到田地， $⊙ O$ 与水面交于点B，C，且点B，C，P在同一直线上，且 $∠ P A C = ∠ P B A$ ，若点P到点C的距离为32m，立式水轮 $⊙ O$ 的最低点到水面的距离为2m.连接 $A C ， A B$ .

(1)、求证： $A P$ 是 $⊙ O$ 的切线；

(2)、请求出水槽 $A P$ 的长度.

查看试题解析
22. 2022年在中国举办的冬奥会和残奥会令世界瞩目，冬奥会和残奥会的吉祥物冰墩墩和雪容融家喻户晓，成为热销产品.某商家以每套34元的价格购进一批冰墩墩和雪容融套件.若该产品每套的售价是48元时，每天可售出200套；若每套售价提高2元，则每天少卖4套.

(1)、设冰墩墩和雪容融套件每套售价定为x元时，求该商品销售量y与x之间的函数关系式；

(2)、求每套售价定为多少元时，每天销售套件所获利润W最大，最大利润是多少元？

(3)、如果每天的利润要达到5920元，并且尽可能的让利于顾客，则每套的售价应该定为多少元？

查看试题解析
23. 如图，抛物线 $y = x^{2} + b x + c$ 与直线 $y = x + m$ 交于点A和点B $(2 ， 5)$ ，且点A在 $x$ 轴上.

(1)、求抛物线的解析式.

(2)、点 $M (x_{M} ， y_{M})$ 与点 $N (3 ， y_{N})$ 是抛物线上两点.若 $y_{M}$ > $y_{N}$ ，求 $x_{M}$ 的取值范围.

(3)、点 $E ， F$ 为抛物线上两点（点E在点F的左侧），且到对称轴的距离分别为3个单位长度和5个单位长度，点Q为抛物线上点 $E ， F$ 之间（含点 $E ， F$ ）的一个动点，求点Q的纵坐标 $y_{Q}$ 的取值范围.

查看试题解析