河南省2023年中考数学模拟试卷
试卷更新日期:2023-04-06 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 如图,正方体的展开图中对面数字之和相等,则-xy=( )
 A、9 B、-9 C、-6 D、-83. 如图,直线AB和CD相交于O点,OE⊥CD,∠EOF=142°,∠BOD:∠BOF=1:3,则∠AOF的度数为( )
A、9 B、-9 C、-6 D、-83. 如图,直线AB和CD相交于O点,OE⊥CD,∠EOF=142°,∠BOD:∠BOF=1:3,则∠AOF的度数为( ) A、138° B、128° C、117° D、102°4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,菱形的对角线 , 相交于点, , 分别是 , 边的中点,连接.若 , , 则菱形的周长为( )
A、138° B、128° C、117° D、102°4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,菱形的对角线 , 相交于点, , 分别是 , 边的中点,连接.若 , , 则菱形的周长为( ) A、4 B、 C、 D、286. 关于的一元二次方程根的情况,下列说法正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定7. 某射击运动员训练射击5发子弹,成绩(单位:环)分别为:8,7,9,10,9,则该运动员练习射击成绩的众数是( )A、7 B、8 C、9 D、108. 双流区坚持教育优先发展,过去5年,新改扩建幼儿园、中小学73所,新增学位47000座,极大满足了人民群众对优质教育的需求.数据47000用科学记数法表示为( )A、47×103 B、4.7×104 C、4.7×105 D、0.47×1059. 如图,在平面直角坐标系中,点在轴的正半轴上,在第一象限,且△是等边三角形.在射线上取点 , , , 分别以 , , 为边作等边三角形△ , △ , 使得 , , , 在同一直线上,该直线交轴于点.若 , , 则点的横坐标是( )
A、4 B、 C、 D、286. 关于的一元二次方程根的情况,下列说法正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定7. 某射击运动员训练射击5发子弹,成绩(单位:环)分别为:8,7,9,10,9,则该运动员练习射击成绩的众数是( )A、7 B、8 C、9 D、108. 双流区坚持教育优先发展,过去5年,新改扩建幼儿园、中小学73所,新增学位47000座,极大满足了人民群众对优质教育的需求.数据47000用科学记数法表示为( )A、47×103 B、4.7×104 C、4.7×105 D、0.47×1059. 如图,在平面直角坐标系中,点在轴的正半轴上,在第一象限,且△是等边三角形.在射线上取点 , , , 分别以 , , 为边作等边三角形△ , △ , 使得 , , , 在同一直线上,该直线交轴于点.若 , , 则点的横坐标是( ) A、 B、 C、256 D、10. 某项工作,已知每人每天完成的工作量相同,且一个人完成需12天.若m个人共同完成需n天,选取6组数对 ,在坐标系中进行描点,则正确的是()A、
A、 B、 C、256 D、10. 某项工作,已知每人每天完成的工作量相同,且一个人完成需12天.若m个人共同完成需n天,选取6组数对 ,在坐标系中进行描点,则正确的是()A、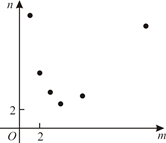 B、
B、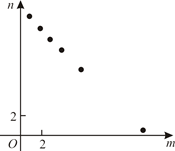 C、
C、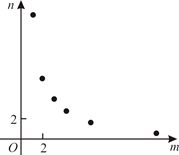 D、
D、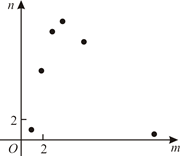
二、填空题
-
11. 写出一个随的增大而减小,且交轴于正半轴的一次函数.12. 若 无解,则a的取值范围是.13. 将如图所示的两个转盘(A转盘被分成三等份,B转盘被分成四等份)各转动一次,当转盘停止后,指针所在区域(指针指向区域分界线时,需重新转动转盘)的数字之和为3的倍数的概率是.
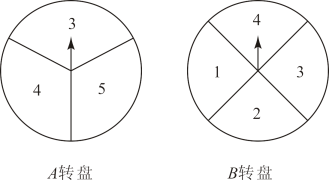 14. 如果用70厘米的铅丝做成一个半径为20厘米的扇形,那么这个扇形的面积等于平方厘米.15. 如图,在 中, , , .点 是 上一动点,以 为斜边向右侧作等腰直角三角形 ,使 ,连接 .
14. 如果用70厘米的铅丝做成一个半径为20厘米的扇形,那么这个扇形的面积等于平方厘米.15. 如图,在 中, , , .点 是 上一动点,以 为斜边向右侧作等腰直角三角形 ,使 ,连接 .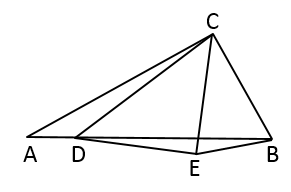 (1)、若点 恰好落在 上,则 的值为;(2)、线段 的最小值为 .
(1)、若点 恰好落在 上,则 的值为;(2)、线段 的最小值为 .三、解答题
-
16. 计算:-|-1|+.17. 某学校为了解疫情期间学生在家体育锻炼情况,从全体学生中随机抽取若干学生进行调查,以下是根据调查数据绘制的统计图表的一部分,根据信息回答下列问题,
组别
平均每日体育锻炼时间(分)
人数
 (1)、本次调查共抽取名学生.(2)、抽查结果中,组有人.(3)、在抽查得到的数据中,中位数位于组(填组别).(4)、若这所学校共有学生人,则估计平均每日锻炼超过分钟有多少人?18. 如图,在平面直角坐标系中,点在第一象限且点到轴、轴的距离分别是、 , 若反比例函数的图象经过点、点.
(1)、本次调查共抽取名学生.(2)、抽查结果中,组有人.(3)、在抽查得到的数据中,中位数位于组(填组别).(4)、若这所学校共有学生人,则估计平均每日锻炼超过分钟有多少人?18. 如图,在平面直角坐标系中,点在第一象限且点到轴、轴的距离分别是、 , 若反比例函数的图象经过点、点. (1)、求出点的坐标及反比例函数的解析式;(2)、过点作垂直于轴,过点作垂直于轴,垂足分别是点、点 , 和交于点 , 连接、 , 求证:;(3)、连接、、.求的面积.19. 20年月日,第五届全国青少年无人机大赛(安徽省赛)在合肥开赛,无人机从地面处起飞,、分别为距离点米的两处监控点,且、、三点在同一条直线上.某团队操作的无人机从点垂直起飞到达处时,在监控点测得点的仰角为 , 秒钟后,无人机直线上升到处,在监控点测得点的仰角为 , 求无人机从到的平均速度.(参考数据: , , , )
(1)、求出点的坐标及反比例函数的解析式;(2)、过点作垂直于轴,过点作垂直于轴,垂足分别是点、点 , 和交于点 , 连接、 , 求证:;(3)、连接、、.求的面积.19. 20年月日,第五届全国青少年无人机大赛(安徽省赛)在合肥开赛,无人机从地面处起飞,、分别为距离点米的两处监控点,且、、三点在同一条直线上.某团队操作的无人机从点垂直起飞到达处时,在监控点测得点的仰角为 , 秒钟后,无人机直线上升到处,在监控点测得点的仰角为 , 求无人机从到的平均速度.(参考数据: , , , ) 20. 新冠肺炎突袭,防疫物资紧缺成为各国急需解决的难题,作为一个负责任大国,中国向各国验发出口防疫物资,深圳海关现要验发万件物资.为了尽快把防疫物资发往各国,深圳海关把工作效率提高到原计划的倍,结果比原计划提前小时完成了验发出口防疫物资.(1)、求原计划每小时验发出口多少万件防疫物资?(2)、中国将第一批次援助巴基斯坦防疫物资打包成件.现计划租用甲、乙两种飞机共架,将这批口罩和防护服全部运往巴基斯坦,且乙种飞机数量不少于甲种飞机的.如果甲种飞机每架需付运输费万元,乙种飞机每架需付运输费万元,在租用甲、乙两种飞机时,应该如何安排可使运输费最少?最少运输费是多少万元?21. 某超市为了销售一种新型饮料,对月销售情况作了如下调查,结果发现每月销售量瓶与销售单价元满足一次函数关系.所调查的部分数据如表:已知每瓶进价为元,每瓶利润销售单价进价
20. 新冠肺炎突袭,防疫物资紧缺成为各国急需解决的难题,作为一个负责任大国,中国向各国验发出口防疫物资,深圳海关现要验发万件物资.为了尽快把防疫物资发往各国,深圳海关把工作效率提高到原计划的倍,结果比原计划提前小时完成了验发出口防疫物资.(1)、求原计划每小时验发出口多少万件防疫物资?(2)、中国将第一批次援助巴基斯坦防疫物资打包成件.现计划租用甲、乙两种飞机共架,将这批口罩和防护服全部运往巴基斯坦,且乙种飞机数量不少于甲种飞机的.如果甲种飞机每架需付运输费万元,乙种飞机每架需付运输费万元,在租用甲、乙两种飞机时,应该如何安排可使运输费最少?最少运输费是多少万元?21. 某超市为了销售一种新型饮料,对月销售情况作了如下调查,结果发现每月销售量瓶与销售单价元满足一次函数关系.所调查的部分数据如表:已知每瓶进价为元,每瓶利润销售单价进价单价元
销售量瓶
(1)、求关于的函数表达式.(2)、该新型饮料每月的总利润为元 , 求关于的函数表达式,并指出单价为多少元时利润最大,最大利润是多少元?(3)、由于该新型饮料市场需求量较大,厂家进行了提价.此时超市发现进价提高了元,每月销售量与销售单价仍满足第(1)问函数关系,当销售单价不超过元时,利润随着x的增大而增大,求的最小值.