海南省澄迈县2023年中考数学第一次模拟试题
试卷更新日期:2023-04-06 类型:中考模拟
一、单选题
-
1. 2023的相反数等于( )A、2023 B、 C、 D、2. 成人体内成熟的红细胞的平均直径一般为0.000007245m,数0.000007245用科学记数法表示( )A、 B、 C、 D、3. 如图是由6个相同的小立方块搭成的几何体,那么这个几何体从上面看是( )
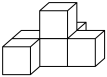 A、
A、 B、
B、 C、
C、 D、
D、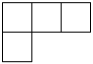 4. 将不等式的解集表示在数轴上,正确的是( )A、
4. 将不等式的解集表示在数轴上,正确的是( )A、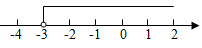 B、
B、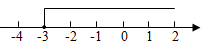 C、
C、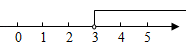 D、
D、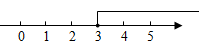 5. 如图, , , 则( )
5. 如图, , , 则( )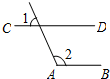 A、 B、 C、 D、6. 已知一组数据:2,5,4,8,7,7,则这组数据的中位数和众数分别是( )A、5,7 B、6,7 C、7,7 D、6,57. 分式方程的解是( )A、x=3 B、x=-3 C、x=-1 D、x=18. 如图,在中, , .将绕点O逆时针方向旋转 , 得到 , 连接.则线段的长为( )
A、 B、 C、 D、6. 已知一组数据:2,5,4,8,7,7,则这组数据的中位数和众数分别是( )A、5,7 B、6,7 C、7,7 D、6,57. 分式方程的解是( )A、x=3 B、x=-3 C、x=-1 D、x=18. 如图,在中, , .将绕点O逆时针方向旋转 , 得到 , 连接.则线段的长为( ) A、2 B、 C、3 D、9. 已知是的反比例函数,如表给出了与的一些值,表中处的数为( )A、 B、 C、 D、10. 如图,C,D在⊙O上,AB是直径,∠D=64°,则∠BAC=( )
A、2 B、 C、3 D、9. 已知是的反比例函数,如表给出了与的一些值,表中处的数为( )A、 B、 C、 D、10. 如图,C,D在⊙O上,AB是直径,∠D=64°,则∠BAC=( )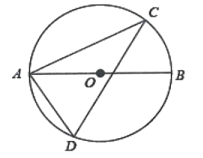 A、64° B、34° C、26° D、24°11. 如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )
A、64° B、34° C、26° D、24°11. 如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( ) A、 B、8 C、 D、612. 如图,在中,点D和E分别是边和的中点,连接 , 与交于点O,若的面积为1,则的面积为( )
A、 B、8 C、 D、612. 如图,在中,点D和E分别是边和的中点,连接 , 与交于点O,若的面积为1,则的面积为( )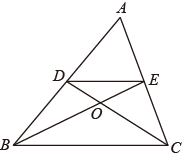 A、6 B、9 C、12 D、13.5
A、6 B、9 C、12 D、13.5二、填空题
-
13. 因式分解:.14. 正十边形的每个内角等于度15. 如图,点为内一点,分别作出点关于 , 的对称点 , , 连结交于 , 交于 , 若线段的长为 , 则的周长为.
 16. 如图,在平面直角坐标系中,点A,B,C的坐标分别为 , , . 点M从坐标原点O出发,第一次跳跃到点 , 使得点与点O关于点A成中心对称;第二次跳跃到点 , 使得点与点关于点B成中心对称;第三次跳跃到点 , 使得点与点关于点C成中心对称;第四次跳跃到点 , 使得点与点关于点A成中心对称;…,依此方式跳跃,点的坐标是 .
16. 如图,在平面直角坐标系中,点A,B,C的坐标分别为 , , . 点M从坐标原点O出发,第一次跳跃到点 , 使得点与点O关于点A成中心对称;第二次跳跃到点 , 使得点与点关于点B成中心对称;第三次跳跃到点 , 使得点与点关于点C成中心对称;第四次跳跃到点 , 使得点与点关于点A成中心对称;…,依此方式跳跃,点的坐标是 .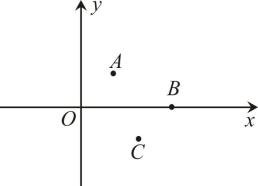
三、解答题
-
17. 计算:(1)、;(2)、.18. 火车站北广场将于2022年底投入使用,计划在广场内种植A,B两种花木共6600棵,若A花木数量是B花木数量的2倍少600棵.(1)、A,B两种花木的数量分别是多少棵?(2)、如果园林处安排25人同时种植这两种花木,每人每天能种植A花木70棵或B花木60棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?19. 某校在“爱心捐款”活动中,同学们都献出了自己的爱心,他们的捐款额有5元、10元、15元、20元四种情况,根据随机抽样统计数据绘制了图1和图2两幅尚不完整的统计图.请你根据图中信息解答下列问题:
 (1)、本次抽样的学生人数是 , 捐款金额的中位数是;(2)、捐款10元的人数是.(3)、该校学生总人数为1000人,请估计该校一共捐款多少元?20. 如图,是的直径,为⨀O上一点,平分交⨀O于点 , 过点作交的延长线于点.
(1)、本次抽样的学生人数是 , 捐款金额的中位数是;(2)、捐款10元的人数是.(3)、该校学生总人数为1000人,请估计该校一共捐款多少元?20. 如图,是的直径,为⨀O上一点,平分交⨀O于点 , 过点作交的延长线于点.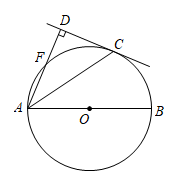 (1)、求证:是的切线.(2)、若 , , 求半径.21. 是边长为4的等边三角形,是等腰三角形, , , 以F为顶点作一个60°的角,角的两边分别交射线CA,BC于点D、E两点,连接DE.
(1)、求证:是的切线.(2)、若 , , 求半径.21. 是边长为4的等边三角形,是等腰三角形, , , 以F为顶点作一个60°的角,角的两边分别交射线CA,BC于点D、E两点,连接DE. (1)、如图1,若D、E两点在线段CA,BC的延长线上.
(1)、如图1,若D、E两点在线段CA,BC的延长线上.①求证:;
②试写出线段AD、BE、DE之间的数量关系,并说明理由;
(2)、如图2,若D、E两点在线段CA,BC上,求的周长.22. 如图,已知抛物线的图象与x轴交于点A(1,0),B(-3,0),与y轴的正半轴交于点C. (1)、求该抛物线的解析式;(2)、点D是线段上一动点,过点D作y轴的平行线,与交于点E,与抛物线交于点F.
(1)、求该抛物线的解析式;(2)、点D是线段上一动点,过点D作y轴的平行线,与交于点E,与抛物线交于点F.①连接 , 当的面积最大时,求此时点F的坐标;
②探究是否存在点D使得为直角三角形?若存在,求出点F的坐标;若不存在,说明理由.