（人教版）2022-2023学年度第二学期七年级数学 坐标方法的简单应用 期中复习

试卷更新日期：2023-04-05 类型：复习试卷

进入 出卷网 下载

一、单选题

  • 1. 以下能够准确表示我校地理位置的是（    ）
    A、离宁波市主城区10千米 B、在江北区西北角 C、在海曙以北 D、东经120.5° ， 北纬29.8°

    查看试题解析

  • 2. 如图，在围棋棋盘上有3枚棋子，如果黑棋①的位置用有序数对(0 ， −1)表示，黑棋②的位置用有序数对(−3 ， 0)表示，则白棋③的位置可用有序数对表示为（    ）

    A、(2 ， 1) B、(−1 ， 2) C、(−2 ， 1) D、(1 ， −2)

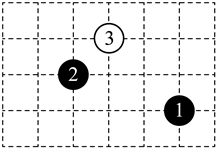    查看试题解析

  • 3. 根据下列表述，不能确定具体位置的是（   ）
    A、某电影院1号厅的3排4座 B、慈溪市孙塘北路824号 C、某灯塔南偏西30°方向 D、东经108°，北纬53°

    查看试题解析

  • 4. 下列不能确定点的位置的是（  ）
    A、东经122° ， 北纬43.6° B、礼堂6排22号 C、地下车库负二层 D、港口南偏东60°方向上距港口10海里

    查看试题解析

  • 5. 如果电影院里的5排7座用(5，7)表示，那么7排8座可表示为（ ）
    A、(5，7) B、(7，8) C、(8，7) D、(7，5)

    查看试题解析

  • 6. 平面直角坐标系中，点A（﹣1，3），B（2，1），经过点A的直线a∥x轴，点C是直线a上的一个动点，当线段BC的长度最短时，点C的坐标为（   ）
    A、（﹣1，1） B、（3，2） C、（2，3） D、（2，﹣1）

    查看试题解析

  • 7. 若点A（3，5），AB∥y轴，且AB＝2，则B点坐标为（   ）
    A、（3，3） B、（1，5）或（5，5） C、（5，5） D、（3，3）或（3，7）

    查看试题解析

  • 8. 如图，第二象限有两点A(m+3 ， n) ， B(m ， n−2) ， 将线段AB平移，使点A，B分别落在两条坐标轴上，则平移后点B的对应点的坐标是（  ）

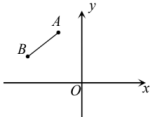    A、(3 ， 0)或(0 ， 2) B、(−3 ， 0)或(0 ， 2) C、(−3 ， 0)或(0 ， −2) D、(3 ， 0)或(0 ， −2)

    查看试题解析

  • 9. 如图，在平面直角坐标系中，正方形ABCD的边长为2，点A坐标为（-2，1），沿某一方向平移后点A1的坐标为（4，2），则点C1的坐标为（  ）

    A、（2，3） B、（2，4） C、（3，4） D、（3，3）

    查看试题解析

  • 10. 平面直角坐标系中，已知A(−3 ， 1) ， B(1 ， −2) ， 作AC//x轴交y轴于点C，点D在直线AC上，则线段BD长度的最小值是（ ）
    A、2 B、3 C、4 D、不存在

    查看试题解析

二、填空题

  • 11. 某校教学楼在校门的正北200m处，实验楼在教学楼正西100m处，若实验楼的坐标为(−100 ， 0) ， 则校门的坐标为 ．

    查看试题解析

  • 12. 春节期间，张强和李明去电影院看抗美援朝电影《长津湖之水门桥》.若将张强电影票上的“4排5座”记作（4，5），则李明电影票上的“6排4座”可记作.

    查看试题解析

  • 13. 将点B (-3， 2)先向右平移m个单位长度，再向上平移n个单位后得到点B.(-1，5)，则mn的值为

    查看试题解析

  • 14. 若直线AB∥x轴，A(2 ， 1)且线段AB=2 ， 则点B的坐标是 ．

    查看试题解析

  • 15. 同学们玩过五子棋吗？它的比赛规则是只要同色5子先连成一条直线就算胜．如图是两人玩的一盘棋，若白棋A的位置是(1 ， −5) ， 黑棋B的位置是(3 ， −5) ， 现轮到黑棋走，你认为黑棋放在位置就获得胜利了．

    查看试题解析

三、解答题

  • 16. 如图所示的是某市区几个旅游景点的示意图（图中每个小正方形的边长为1个单位长度），若海洋极地公园的坐标为（4，0），大唐芙蓉园的坐标为（2，-1），请建立平面直角坐标系，并用坐标表示其他景点的位置．

    查看试题解析

  • 17. 建立平面直角坐标系，依次描出点A（-2，0），B（0，-3），C（-3，-5），连接AB、BC、CA．求△ABC的面积．

    查看试题解析

  • 18. 已知四边形AOCD是放置在平面直角坐标系内的梯形，其中O是坐标原点，点A，C，D的坐标分别为（0，8），（5，0），（3，8）.若点P在梯形内，且△PAD的面积等于△POC的面积，△PAO的面积等于△PCD的面积. 求点P的坐标.

    查看试题解析

四、综合题

  • 19.    
    (1)、计算：(−1)2021+16+−273−(−3)2+|3−2|
    (2)、如图所示的是某学校的平面示意图，已知旗杆的位置是(−1 ， 2) ， 实验室的位置是(2 ， 3) ．

    ①根据所给条件建立适当的平面直角坐标系，并用坐标表示食堂，宿舍楼和大门的位置．

    ②已知办公楼的位置是(−2 ， 1) ， 教学楼的位置是(3 ， 1) ， 在①中所画的图中标出办公楼和教学楼的位置．

    查看试题解析

  • 20. 如图是某学校的平面示意图，已知旗杆的位置是（-2，3），实验室的位置是（1，4）

    (1)、根据所给条件在图中建立适当的平面直角坐标系；
    (2)、用坐标表示位置：食堂 ， 图书馆 ．
    (3)、已知办公楼的位置是（-2，1），教学楼的位置是（2，2），在图中标出办公楼和教学楼的位置；

    查看试题解析

  • 21. 如图，在平面直角坐标系中，三角形ABC的三个顶点都在网格的格点上，其中点C的坐标为（1，2）．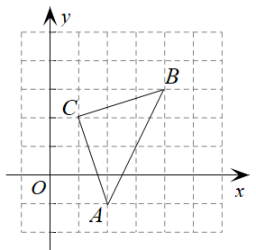

    (1)、点A的坐标为 ， 点B的坐标为；
    (2)、将三角形ABC先向左平移2个单位长度，再向上平移1个单位长度，得到三角形A'B'C'，请画出平移后的三角形A'B'C'，并写出点A'，B'，C'的坐标．

    查看试题解析

  • 22. 如图，△ABC中任意一点P(x0 ， y0)经平移后对应点为P1(x0+5 ， y0−3)

    (1)、点P向平移5个单位长度，再向平移3个单位长度．（选填“上”、“下”、“左”、“右”）
    (2)、按上面的平移方式，将△ABC平移得到△A1B1C1 ， 画出平移后的△A1B1C1 ， 并求出A1 ， B1 ， C1的坐标．

    查看试题解析

  • 23. 对于平面直角坐标系xOy中的点P（a，b），若点P′的坐标为（a＋kb，ka＋b）（其中k为常数，且k≠0），则称点P′为点P的“k属派生点”.

    例如：P（1，4）的“2属派生点”为P′（1＋2×4，2×1＋4），即P′（9，6）.

    (1)、点P（－1，6）的“2属派生点”P′的坐标为；
    (2)、若点P的“3属派生点”P′的坐标为（6，2），则点P的坐标；
    (3)、若点P在x轴的正半轴上，点P的“k属派生点”为P′点，且线段PP′的长度为线段OP长度的2倍，求k的值.

    查看试题解析