（人教版）2022-2023学年度第二学期七年级数学 平行线及其判定 期中复习
试卷更新日期：2023-04-05 类型：复习试卷
一、单选题
-
1. 如图，两直线AB、CD平行，则（ ）
A、630° B、720° C、900° D、1080°2. 下面给出的结论中，①立方根等于算术平方根的是0；②在同一个平面内，经过一点可以画一条直线和已知直线平行；③；④若 ， 则；⑤邻补角的两条角平分线构成一个直角；⑥经过一个已知点只能画一条直线和已知直线垂直；⑦若ab， ， 那么；⑧是的平方根，其中不正确的说法有（ ）A、4个 B、5个 C、6个 D、7个3. 一个三角板和一个直尺拼接成如图所示的图形，其中 ，则 的度数是（ ）.
A、10° B、45° C、37.5° D、15°4. 按如图所示的方式放置直角三角板和直尺，若∠1=25°，则∠2的度数为（ ）
A、50° B、45° C、40° D、35°5. 如图所示，AB∥CD，E为AB上方一点，FB， HG分别为∠EFG，∠EHD的角平分线，若∠E+2∠G=150° ，则∠EFG的度数为（ ）
A、90° B、95° C、100° D、150°6. 下列说法正确的是（ ）A、有且只有一条直线与已知直线平行 B、垂直于同一条直线的两条直线互相垂直 C、从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离 D、在平面内过一点有且只有一条直线与已知直线垂直7. 如图，两只手的食指和拇指在同一平面内，在以下四种摆放方式中，它们构成的一对角可以看成同位角的是（ ）A、
B、
C、
D、
8. 如图，在下列四组条件中，能判定AB∥CD的是（ ）
A、∠D = ∠A B、∠B = ∠C C、∠B + ∠C = 180° D、∠A + ∠B = 180°9. 如图，∠1＝∠2，∠DAB＝∠BCD.给出下列结论：①AB∥DC；②AD∥BC；③∠B＝∠D；④∠D＝2∠DAB.其中，正确的结论有（ ）
A、1个 B、2个 C、3个 D、4个10. 如图，下列推理错误的是（ ）
A、∵∠1＝∠3∴a∥b B、∵∠1＝∠2∴a∥b C、∵∠3＝∠5∴c∥d D、∵∠2+∠4＝180°∴c∥d二、填空题
-
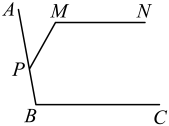
11. 如图，∠ABC=100°， ， 动点P在射线BA上从点B开始沿BA方向运动，连接MP，当∠PMN=120°时，∠BPM的度数为 ．
12. 如图，直线m∥n，∠AOB的两边分别于直线n、m交于点A、B，已知∠AOB＝120°，则∠2﹣∠1＝.
13. 如图，ABCD，分别平分 ， ， 与的反向延长线交于点 ， ， 则°.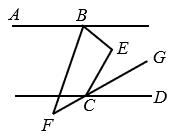
14. 如图，下列条件中能推出a∥b的有.
①∠3=∠5， ②∠1=∠7，③∠2+∠5=180°，④∠1+∠4=180°.
15. 如图，在条件：①；②；③；④中，能判断的条件是（填序号）．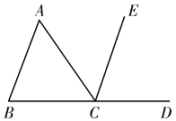
三、解答题
-
16. 如图，AB⊥BF，CD⊥BF，∠1＝∠2，试说明∠3＝∠E.
证明：∵AB⊥BF，CD⊥BF（已知），
∴∠ABD＝∠CDF＝ （ ），
∴ （ ）
∵∠1＝∠2（已知），
∴ （ ）
∴ （ ）
∴∠3＝∠E（ ）
17. 如图，AB⊥ BC，BC⊥ CD，且∠ 1=∠ 2，证明：EB∥ CF
18. 如图，已知 ， D是平分线上一点，与交于点E，若 ， 求证： ．
请将下面的证明过程补充完整：
证明：∵平分 ，
∴ ▲ ▲ ▲ （角平分线定义）．
又∵ ，
∴ ▲ ．
∴（ ）．
四、综合题
-
19.
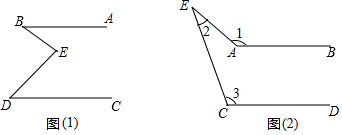(1)、如图①，若∠B+∠D=∠BED，试猜想AB与CD的位置关系，并说明理由；(2)、如图②，要想得到AB∥CD，则∠1、∠2、∠3之间应满足怎样的数量关系，试说明理由.20. 已知，直线 ， 直线和 ， 分别交于C，D点，点A，B分别在直线 ， 上，且位于直线的左侧，动点P在直线上，且不和点C，D重合.
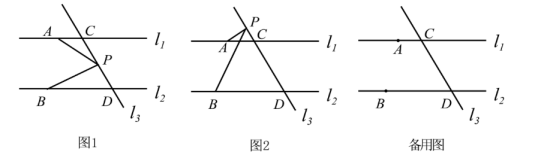(1)、如图1，当动点P在线段CD上运动时，求证：∠APB＝∠CAP＋∠DBP；(2)、如图2，当动点P在点C上方运动时（P，A，B不在同一直线上），请写出∠APB，∠CAP，∠DBP之间的数量关系，并选择其中一种的数量关系说明理由.
