（人教版）2022-2023学年度第二学期七年级数学 相交线 期中复习
试卷更新日期：2023-04-05 类型：复习试卷
一、单选题
-
1. 如图，AB，CD交于点O，OE⊥AB于点O，则下列不正确的是（ ）
A、∠AOC与∠BOD是对顶角 B、∠BOD和∠DOE互为余角 C、∠AOC和∠DOE互为余角 D、∠AOE和∠BOC是对顶角 -
2. 如图，直线a，b被c，d所截，且c⊥a，c⊥b，∠1＝57°，则∠2的度数为（ ）
A、113° B、120° C、123° D、147° -
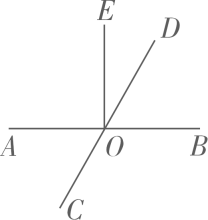
3. 如图所示，已知点O是直线CD上的一点，∠AOC＝30°，OB平分∠AOD，则∠BOD的度数是（ ）
A、75° B、65° C、55° D、45° -
4. 点P为直线外一点，点A、B、C为直线上三点， ， ， ， 则P到直线的距离为（ ）A、 B、 C、小于 D、不大于
-
5. 如图，小华同学的家在点P处，他想尽快到达公路边去接从外地回来的外婆，他选择沿线段PC去公路边，他的这一选择用到的数学知识是（ ）
A、两点确定一条直线 B、两点之间直线最短 C、垂线段最短 D、以上说法都不对 -
6. 如图，已知AM是△ABC的中线，点P是AC边上一动点，若△ABC的面积为10，AC=4，则MP的最小值为（ ）
A、5 B、2.5 C、1.4 D、1.25 -
7. 下列说法：①在同一平面内，垂直于同一条直线的两条直线互相平行；②两条直线被第三条直线所截，内错角相等；③如果直线a∥b，b∥c，那么a∥c；④连结直线外一点与直线上各点的所有线段中，垂线段最短；⑤同旁内角的角平分线互相垂直．其中正
确的是（ ）
A、①③④ B、①②⑤ C、②③④ D、②③⑤ -
8. 若∠1与∠2是同旁内角，则（ ）A、∠1与∠2不可能相等 B、∠1与∠2一定互补 C、∠1与∠2可能互余 D、∠1与∠2一定相等
-
9. 如图，下列说法错误的是（ ）
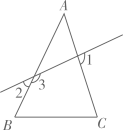A、∠C与∠1是内错角 B、∠2与∠A是内错角 C、∠A与∠B是同旁内角 D、∠A与∠3是同位角 -
10. 若∠1与∠2的关系是同位角，∠1=30°，则∠2=（ ）A、30° B、150° C、50°或130° D、不确定
二、填空题
-
11. 如图，直线AB、CD、EF相交于一点，∠1=50°，∠2=62°，则∠COF=度.
-
12. 如图，已知直线 ，直线 分别与直线 ， 相交， ，则 的度数为°.
-
13. 如图， ， ， 则表示点到直线所在直线的距离为线段的长度．
-
14. 如图，ABCD，平分交于 ， ， ， ， 则下列结论：①；②；③；④平分 ， 其中正确的是.
-
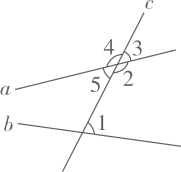
15. 已知直线a、b被直线c所截，则与∠1是内错角关系的是.
三、解答题
-
16. 完成下面的证明过程．
已知：如图，点E、F分别在AB、CD上，AD分别交EC、BF于点H、G，∠1＝∠2，∠B＝∠C．求证∠A＝∠D．
证明：∵∠1＝∠2（已知），
∠2＝∠AGB（ ），
∴∠1＝ ．
∴EC∥BF（ ）．
∴∠B＝∠AEC（ ）．
又∵∠B＝∠C（已知），
∴∠AEC＝ ．
∴ （ ）．
∴∠A＝∠D（ ）．
-
17. 如图，相交于点 ， ， 为垂足，若 ， 求的度数.
-
18. 如图所示，∠1与∠2，∠3与∠4．∠1与∠4分别是什么位置关系？分别是哪两条直线被哪一条直线所截形成的？
四、综合题
-
19. 如图，已知直线 ， 的顶点在上，两边分别与、相交于点 ， 点 ， 射线始终在的内部.
(1)、当时，①求的度数；②直接写出与的数量关系；
(2)、若的度数为 ， 且 ， 其余条件不变，猜想与的数量关系，并说明理由. -
20. 如图， 于点 ， 于点 ，且 .
(1)、试判断 与 的位置关系，并说明理由.(2)、若 ，求 的度数. -
21. 如图，在△ABC中，CD⊥AB，垂足为D，点E在BC上，EF⊥AB，垂足为F．
(1)、CD与EF平行吗？请说明理由；(2)、如果∠1＝∠2，且∠3＝110°，求∠ACB的度数． -
22. 如图所示，在直角三角形ABC中，∠C= 90°，DE⊥AC交AC于点E，交AB于点D．
(1)、请分别写出当BC，DE被AB所截时，∠B的同位角、内错角和同旁内角；(2)、试说明∠1=∠2=∠B的理由． -
23. 光线在不同的介质中传播的速度是不同的，因此当光线从水中射向空气时，要发生折射，由于折射率相同，所以在水中平行的光线，在空气中也是平行的．如图所示，恰有两束平行光线从水中射向空气，∠1＝30°，∠2＝130°．
(1)、分别指出图中的两对同位角，一对内错角；(2)、求∠3，∠5，∠8的度数，并判断∠1和∠4是否互补．
