备考2023年中考数学绍兴卷变式阶梯训练:21-24题
试卷更新日期:2023-04-05 类型:三轮冲刺
一、第二十一题
-
1. 如图,半径为6的⊙O与Rt△ABC的边AB相切于点A,交边BC于点C,D,∠B=90°,连结OD,AD.
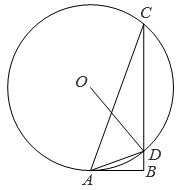 (1)、若∠ACB=20°,求 的长(结果保留π).(2)、求证:AD平分∠BDO.2. 如图, 是 的内接三角形, 为 直径, , 平分 ,交 于点 ,交 于点 ,连接 .
(1)、若∠ACB=20°,求 的长(结果保留π).(2)、求证:AD平分∠BDO.2. 如图, 是 的内接三角形, 为 直径, , 平分 ,交 于点 ,交 于点 ,连接 . (1)、求证: ;(2)、若 ,求 的长(结果保留 ).3. 如图,已知PC平分∠MPN,点O是PC上任意一点,PM与⊙O相切于点E,交PC于A、B两点.
(1)、求证: ;(2)、若 ,求 的长(结果保留 ).3. 如图,已知PC平分∠MPN,点O是PC上任意一点,PM与⊙O相切于点E,交PC于A、B两点.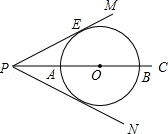 (1)、求证:PN与⊙O相切;(2)、如果∠MPC=30°,PE=2 ,求劣弧 的长.4. 如图,在△ABC中,AB=AC,∠BAC=54°,以AB为直径的⊙O分别交AC、BC于点D、E,过点B作直线BF,交AC的延长线于点F.
(1)、求证:PN与⊙O相切;(2)、如果∠MPC=30°,PE=2 ,求劣弧 的长.4. 如图,在△ABC中,AB=AC,∠BAC=54°,以AB为直径的⊙O分别交AC、BC于点D、E,过点B作直线BF,交AC的延长线于点F. (1)、求证:BE=CE;(2)、若AB=6,求弧DE的长;(3)、当∠F的度数是多少时,BF与⊙O相切,证明你的结论.5. 如图,在Rt△ABC中,∠B=90°,AE平分∠BAC交BC于点E,O为AC上一点,经过点A、E的⊙O分别交AB、AC于点D、F,连接OD交AE于点M.
(1)、求证:BE=CE;(2)、若AB=6,求弧DE的长;(3)、当∠F的度数是多少时,BF与⊙O相切,证明你的结论.5. 如图,在Rt△ABC中,∠B=90°,AE平分∠BAC交BC于点E,O为AC上一点,经过点A、E的⊙O分别交AB、AC于点D、F,连接OD交AE于点M. (1)、求证:BC是⊙O的切线.(2)、若CF=2,sinC= , 求AE的长.6. 如图,点在以为直径的上,平分交于点 , 交于点 , 过点作的切线交的延长线于点.
(1)、求证:BC是⊙O的切线.(2)、若CF=2,sinC= , 求AE的长.6. 如图,点在以为直径的上,平分交于点 , 交于点 , 过点作的切线交的延长线于点.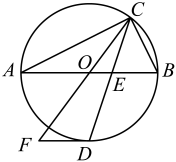 (1)、求证:;(2)、若 , , 求的长.7. 如图,A为⊙O外一点,AO⊥BC,直径BC=12,AO=10,的长为π,点P是BC上一动点,∠DPM=90°,点M在⊙O上,且∠DPM在DP的下方.
(1)、求证:;(2)、若 , , 求的长.7. 如图,A为⊙O外一点,AO⊥BC,直径BC=12,AO=10,的长为π,点P是BC上一动点,∠DPM=90°,点M在⊙O上,且∠DPM在DP的下方. (1)、当sinA=时,求证:AM是⊙O的切线;(2)、求AM的最大长度.
(1)、当sinA=时,求证:AM是⊙O的切线;(2)、求AM的最大长度.二、第二十二题
-
8. 如图,在△ABC中,∠ABC=40°, ∠ACB=90°,AE平分∠BAC交BC于点E.P是边BC上的动点(不与B,C重合),连结AP,将△APC沿AP翻折得△APD,连结DC,记∠BCD=α.
 (1)、如图,当P与E重合时,求α的度数.(2)、当P与E不重合时,记∠BAD=β,探究α与β的数量关系.9. 如图,在 中, ,将 沿着 折叠以后 点正好落在 边上的点 处.
(1)、如图,当P与E重合时,求α的度数.(2)、当P与E不重合时,记∠BAD=β,探究α与β的数量关系.9. 如图,在 中, ,将 沿着 折叠以后 点正好落在 边上的点 处.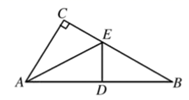 (1)、当 时,求 的度数;(2)、当 , 时,求线段 的长.10. 如图,在平面直角坐标系中,点 为坐标原点,点 、 、 的坐标分别为 、 、 , ,将 沿着射线 翻折,点 落到 轴上点 处.(1)、求点 的坐标;
(1)、当 时,求 的度数;(2)、当 , 时,求线段 的长.10. 如图,在平面直角坐标系中,点 为坐标原点,点 、 、 的坐标分别为 、 、 , ,将 沿着射线 翻折,点 落到 轴上点 处.(1)、求点 的坐标; (2)、动点 以每秒1个单位长度的速度从点 出发沿着线段 向终点 运动,运动时间为 秒,请用含有 的式子表示 的面积,并直接写出 的取值范围;
(2)、动点 以每秒1个单位长度的速度从点 出发沿着线段 向终点 运动,运动时间为 秒,请用含有 的式子表示 的面积,并直接写出 的取值范围; (3)、在(2)的条件下,动点 以每秒2个单位长度的速度从点 出发沿着线段 向终点 运动,动点 以每秒 个单位长度的速度从点 出发沿着 轴正方向运动,点 、 、 同时出发;点 停止时,点 、 也停止运动,当 时,求 的值.
(3)、在(2)的条件下,动点 以每秒2个单位长度的速度从点 出发沿着线段 向终点 运动,动点 以每秒 个单位长度的速度从点 出发沿着 轴正方向运动,点 、 、 同时出发;点 停止时,点 、 也停止运动,当 时,求 的值. 11. 已知D是等边三角形中AB边上一点,将CB沿直线CD翻折得到CE,连接并延长交直线于点F.
11. 已知D是等边三角形中AB边上一点,将CB沿直线CD翻折得到CE,连接并延长交直线于点F. (1)、如图1,若 , 直接写出∠CFE的度数;(2)、如图1,若 , 求AE的长;(3)、如图2,连接BF,当点D在运动过程中,请探究线段AF,BF,CF之间的数量关系,并证明.12. 如图,在△ABC中,E是AB中点,F是AC上一动点,连结EF,将△AEF沿直线EF折叠得△DEF.
(1)、如图1,若 , 直接写出∠CFE的度数;(2)、如图1,若 , 求AE的长;(3)、如图2,连接BF,当点D在运动过程中,请探究线段AF,BF,CF之间的数量关系,并证明.12. 如图,在△ABC中,E是AB中点,F是AC上一动点,连结EF,将△AEF沿直线EF折叠得△DEF. (1)、如图①,若∠B=45°,且点D恰好落在线段BC上,求证:点F为线段AC的中点;(2)、如图②,若△ABC为等边三角形,且边长为4,当点D落在线段CE上时,求AF的长度;(3)、如图③,若△ABC为直角三角形,∠BAC=90°,AC=8.连结AD、BD、CD,若△ACD与△BDC面积相等,且CD=4,求△ABC的面积.13.
(1)、如图①,若∠B=45°,且点D恰好落在线段BC上,求证:点F为线段AC的中点;(2)、如图②,若△ABC为等边三角形,且边长为4,当点D落在线段CE上时,求AF的长度;(3)、如图③,若△ABC为直角三角形,∠BAC=90°,AC=8.连结AD、BD、CD,若△ACD与△BDC面积相等,且CD=4,求△ABC的面积.13. (1)、如图,把沿折叠,使点A落在点处,试探究、与的关系;(2)、如图2,若 , , 作的平分线 , 与的外角平分线交于点 , 求的度数;(3)、如图3,若点落在内部,作 , 的平分线交于点 , 此时 , , 满足怎样的数量关系?并给出证明过程.14. 如图①,在△ABC中,∠C=90°,AC=8cm,BC=6cm.动点P在线段AC上以5cm/s的速度从点A运动到点C.过点P作PD⊥AB于点D,将△APD绕PD的中点旋转180°得到△A'DP.设点P的运动时间为x(s).
(1)、如图,把沿折叠,使点A落在点处,试探究、与的关系;(2)、如图2,若 , , 作的平分线 , 与的外角平分线交于点 , 求的度数;(3)、如图3,若点落在内部,作 , 的平分线交于点 , 此时 , , 满足怎样的数量关系?并给出证明过程.14. 如图①,在△ABC中,∠C=90°,AC=8cm,BC=6cm.动点P在线段AC上以5cm/s的速度从点A运动到点C.过点P作PD⊥AB于点D,将△APD绕PD的中点旋转180°得到△A'DP.设点P的运动时间为x(s).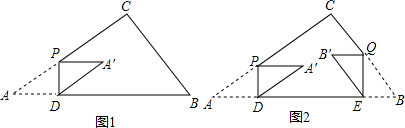 (1)、求点A'落在边BC上时x的值.(2)、设△A'DP和△ABC重叠部分图形周长为y(cm),求y与x之间的函数关系式.(3)、如图②,另有一动点Q与点P同时出发,在线段BC上以5cm/s的速度从点B运动到点C.过点Q作QE⊥AB于点E,将△BQE绕QE的中点旋转180°得到△B'EQ.连结A′B′.当直线A'B'与△ABC的边垂直或平行时,直接写出x的值.
(1)、求点A'落在边BC上时x的值.(2)、设△A'DP和△ABC重叠部分图形周长为y(cm),求y与x之间的函数关系式.(3)、如图②,另有一动点Q与点P同时出发,在线段BC上以5cm/s的速度从点B运动到点C.过点Q作QE⊥AB于点E,将△BQE绕QE的中点旋转180°得到△B'EQ.连结A′B′.当直线A'B'与△ABC的边垂直或平行时,直接写出x的值.三、第二十三题
-
15. 已知函数y=-x2+bx+c(b,c为常数)的图象经过点(0,﹣3),(﹣6,﹣3).(1)、求b,c的值.(2)、当﹣4≤x≤0时,求y的最大值.(3)、当m≤x≤0时,若y的最大值与最小值之和为2,求m的值.16. 已知关于x的二次函数(m是常数).(1)、若该二次函数的图象经过点 ,
①求m的值;②若该二次函数的图象与x轴交于点B,C(点B在点C的左侧),求的面积;
(2)、若该二次函数的图象与y轴交于点P,求点P纵坐标的最大值;17. 如图,二次函数的图象与轴交于 , 两点,与轴交于点. (1)、求二次函数的解析式和图象的对称轴;(2)、若该二次函数在内有最大值 , 求的值.18. 已知二次函数y=ax2+4ax+3a-1的图象开口向下.(1)、若点(m,-9)和(1,-9)是该图象上不同的两点,求m的值.(2)、当-4≤x≤4时,函数的最大值与最小值的差为6,求a的值.19. 已知:二次函数(1)、m为何值时,此抛物线必与x轴相交于两个不同的点;(2)、 m为何值时,这两个交点在原点的左右两边;(3)、 m为何值时,此抛物线的对称轴是y轴;(4)、 m为何值时,这个二次函数有最大值 .20. 已知抛物线经过点 .(1)、求a的值;(2)、若抛物线与y轴的公共点为 , 抛物线与x轴是否有公共点,若有,求出公共点的坐标;若没有,请说明理由;(3)、当时,设二次函数的最大值为M,最小值为N,若 , 求m的值.21. 如图,在平面直角坐标系中,二次函数的图象经过点 , 点 , 与直线交于点 .
(1)、求二次函数的解析式和图象的对称轴;(2)、若该二次函数在内有最大值 , 求的值.18. 已知二次函数y=ax2+4ax+3a-1的图象开口向下.(1)、若点(m,-9)和(1,-9)是该图象上不同的两点,求m的值.(2)、当-4≤x≤4时,函数的最大值与最小值的差为6,求a的值.19. 已知:二次函数(1)、m为何值时,此抛物线必与x轴相交于两个不同的点;(2)、 m为何值时,这两个交点在原点的左右两边;(3)、 m为何值时,此抛物线的对称轴是y轴;(4)、 m为何值时,这个二次函数有最大值 .20. 已知抛物线经过点 .(1)、求a的值;(2)、若抛物线与y轴的公共点为 , 抛物线与x轴是否有公共点,若有,求出公共点的坐标;若没有,请说明理由;(3)、当时,设二次函数的最大值为M,最小值为N,若 , 求m的值.21. 如图,在平面直角坐标系中,二次函数的图象经过点 , 点 , 与直线交于点 . (1)、求二次函数的解析式;(2)、当时,函数有最小值-3,求m的值;(3)、过点作轴,点的横坐标为 . 已知点与点不重合,且线段的长度随的增大而减小.
(1)、求二次函数的解析式;(2)、当时,函数有最小值-3,求m的值;(3)、过点作轴,点的横坐标为 . 已知点与点不重合,且线段的长度随的增大而减小.①求m的取值范围;
②当时,直接写出线段PQ与二次函数的图象有一个交点时m的取值范围.
四、第二十四题
-
22. 如图,在矩形 ABCD中,AB=6,BC=8,动点 E从点A出发,沿边AD,DC向点C运动,A, D关于直线 BE的对称点分别为M,N,连结MN .
 (1)、如图,当E在边AD上且 DE=2时,求 ∠AEM的度数.(2)、当N在BC延长线上时,求DE的长,并判断直线MN与直线BD的位置关系,说明理由.(3)、当直线MN恰好经过点 C 时,求DE的长.23. 已知,在矩形中, , , 动点M从点A出发沿边向点D运动.
(1)、如图,当E在边AD上且 DE=2时,求 ∠AEM的度数.(2)、当N在BC延长线上时,求DE的长,并判断直线MN与直线BD的位置关系,说明理由.(3)、当直线MN恰好经过点 C 时,求DE的长.23. 已知,在矩形中, , , 动点M从点A出发沿边向点D运动.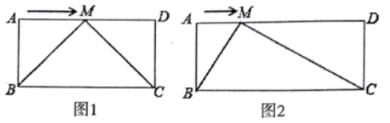 (1)、如图1,当 , 点M运动到边的中点时,请证明;(2)、如图2,当时,点M在运动的过程中,是否存在 , 若存在,请给与证明;若不存在,请说明理由.24. 如图,在四边形ABCD中,AB∥CD,∠A=90°,AB=2,AD=5,P是AD上一动点(点P不与A、D重合),PE⊥BP,PE交DC于点E.
(1)、如图1,当 , 点M运动到边的中点时,请证明;(2)、如图2,当时,点M在运动的过程中,是否存在 , 若存在,请给与证明;若不存在,请说明理由.24. 如图,在四边形ABCD中,AB∥CD,∠A=90°,AB=2,AD=5,P是AD上一动点(点P不与A、D重合),PE⊥BP,PE交DC于点E. (1)、求证:△ABP∽△DPE;(2)、设AP=x,DE=y,求y与x之间的函数关系式,并写出x的取值范围;(3)、请你探索在点P运动的过程中,四边形ABED能否构成矩形?如果能,求出AP的长;如果不能,请说明理由.25. 如图,在平面直角坐标系中,直线 过点 ,过点A作x轴的垂线,垂足为点B,过点A作y轴的垂线,垂足为点C. , 于点D.动点P从点O出发,以每秒2个单位长度的速度向点A运动,动点Q从点A出发.以每秒 个单位长度的速度向点B运动.点P,Q同时开始运动,当点P到达点A时,点P,Q同时停止运动,设运动时间为 ,且 .
(1)、求证:△ABP∽△DPE;(2)、设AP=x,DE=y,求y与x之间的函数关系式,并写出x的取值范围;(3)、请你探索在点P运动的过程中,四边形ABED能否构成矩形?如果能,求出AP的长;如果不能,请说明理由.25. 如图,在平面直角坐标系中,直线 过点 ,过点A作x轴的垂线,垂足为点B,过点A作y轴的垂线,垂足为点C. , 于点D.动点P从点O出发,以每秒2个单位长度的速度向点A运动,动点Q从点A出发.以每秒 个单位长度的速度向点B运动.点P,Q同时开始运动,当点P到达点A时,点P,Q同时停止运动,设运动时间为 ,且 . (1)、求m与k的值;(2)、当点P运动到点D时,求t的值;(3)、连接DQ,点E为DQ的中点,连接PE,当 时,请直接写出点P的坐标.26. 如图,四边形ABCD中,AD//BC, , , ,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.当其中一个动点到达终点时,另一个动点也随之停止运动.过点N作 于点P,连接AC交NP于点Q,连接MQ,设运动时间为t秒( )
(1)、求m与k的值;(2)、当点P运动到点D时,求t的值;(3)、连接DQ,点E为DQ的中点,连接PE,当 时,请直接写出点P的坐标.26. 如图,四边形ABCD中,AD//BC, , , ,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.当其中一个动点到达终点时,另一个动点也随之停止运动.过点N作 于点P,连接AC交NP于点Q,连接MQ,设运动时间为t秒( )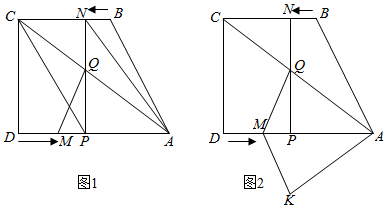 (1)、连接AN,CP,当t为何值时,四边形ANCP为平行四边形;(2)、设四边形DMQC的面积为y,求y与t的函数关系式;(3)、在运动过程中,是否存在某一时刻t,使四边形DMQC的面积与△ABC的面积相等?若存在,求出t的值;若不存在,请说明理由;(4)、将△AQM沿AD翻折,得到△AKM.在运动过程中,是否存在某时刻t,使四边形AQMK为菱形,若存在,求出t的值;若不存在,请说明理由.27. 如图,平行四边形ABCD中,DB= , AB=4,AD=2,动点E,F同时从A点出发,点E沿着A→D→B的路线匀速运动,点F沿着A→B→D的路线匀速运动,当点E,F相遇时停止运动.
(1)、连接AN,CP,当t为何值时,四边形ANCP为平行四边形;(2)、设四边形DMQC的面积为y,求y与t的函数关系式;(3)、在运动过程中,是否存在某一时刻t,使四边形DMQC的面积与△ABC的面积相等?若存在,求出t的值;若不存在,请说明理由;(4)、将△AQM沿AD翻折,得到△AKM.在运动过程中,是否存在某时刻t,使四边形AQMK为菱形,若存在,求出t的值;若不存在,请说明理由.27. 如图,平行四边形ABCD中,DB= , AB=4,AD=2,动点E,F同时从A点出发,点E沿着A→D→B的路线匀速运动,点F沿着A→B→D的路线匀速运动,当点E,F相遇时停止运动. (1)、如图1,设点E的速度为1个单位每秒,点F的速度为4个单位每秒,当运动时间为秒时,设CE与DF交于点P,求线段EP与CP长度的比值;(2)、如图2,设点E的速度为1个单位每秒,点F的速度为个单位每秒,运动时间为x秒,ΔAEF的面积为y,求y关于x的函数解析式,并指出当x为何值时,y的值最大,最大值为多少?(3)、如图3,H在线段AB上且AH=HB,M为DF的中点,当点E、F分别在线段AD、AB上运动时,探究点E、F在什么位置能使EM=HM.并说明理由.28. 如图,在菱形 中, , ,点 从点 出发,沿线段 以每秒1个单位长度的速度向终点 运动,过点 作 于点 ,作 交直线 于点 ,交直线 于点 ,设 与菱形 重叠部分图形的面积为 (平方单位),点 运动时间为 (秒).
(1)、如图1,设点E的速度为1个单位每秒,点F的速度为4个单位每秒,当运动时间为秒时,设CE与DF交于点P,求线段EP与CP长度的比值;(2)、如图2,设点E的速度为1个单位每秒,点F的速度为个单位每秒,运动时间为x秒,ΔAEF的面积为y,求y关于x的函数解析式,并指出当x为何值时,y的值最大,最大值为多少?(3)、如图3,H在线段AB上且AH=HB,M为DF的中点,当点E、F分别在线段AD、AB上运动时,探究点E、F在什么位置能使EM=HM.并说明理由.28. 如图,在菱形 中, , ,点 从点 出发,沿线段 以每秒1个单位长度的速度向终点 运动,过点 作 于点 ,作 交直线 于点 ,交直线 于点 ,设 与菱形 重叠部分图形的面积为 (平方单位),点 运动时间为 (秒).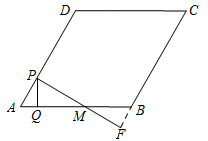 (1)、当点 与点 重合时,求 的值;(2)、当 为何值时, 与 全等;(3)、求 与 的函数关系式;(4)、以线段 为边,在 右侧作等边三角形 ,当 时,求点 运动路径的长.
(1)、当点 与点 重合时,求 的值;(2)、当 为何值时, 与 全等;(3)、求 与 的函数关系式;(4)、以线段 为边,在 右侧作等边三角形 ,当 时,求点 运动路径的长.