备考2023年中考数学绍兴卷变式阶梯训练：17-20题

试卷更新日期：2023-04-05 类型：三轮冲刺

进入出卷网下载

一、第十七题

1.

(1)、计算： $6 \tan 30 ° + {(π + 1)}^{0} - \sqrt{12}$ ．

(2)、解方程组 ${\begin{cases} 2 x - y = 4 ， \\ x + y = 2. \end{cases}$

查看试题解析
2.

(1)、计算：2^-1-2022⁰+ sin30°

(2)、解方程组： ${\begin{cases} x - 3 y = 8 \\ 2 x + 3 y = 7 \end{cases}$

查看试题解析
3.

(1)、计算：sin30°-（ $\sqrt{3}$ -2）⁰+2^-¹；

(2)、解方程组： ${\begin{array}{l} 2 x + y = 2 \\ x + y = 0 \end{array}$ .

查看试题解析
4. 计算：

(1)、计算： $\sqrt{27}$ ﹣3tan60°+（π﹣2）⁰；

(2)、解方程组： ${\begin{array}{l} 2 x + y = 6 \\ x + 2 y = - 3 \end{array}$ .

查看试题解析
5.

(1)、计算： $2^{- 1} + | - 3 | + (\sqrt{3} - 2)^{0} - c o s 60 °$

(2)、解方程组： ${\begin{array}{l} x - 2 y = 5 \\ x + 2 (y - 3) = 1 \end{array}$

查看试题解析
6.

(1)、计算： $\sqrt{8}$ ﹣|﹣2|﹣tan30°+（ $\sqrt{3}$ ）^﹣¹；

(2)、解方程组： ${\begin{array}{l} 4 x + 5 y = 11 \\ 2 x - y = 2 \end{array}$ .

查看试题解析
7.

(1)、计算： $\sqrt{27} - {(- 2)}^{2} + | 1 - \sqrt{3} | + 2 cos 30^{°}$ ；

(2)、解方程组： ${\begin{matrix} \end{matrix} \begin{matrix} x + y = 5 \\ 2 x + 3 y = 11 \end{matrix}$

查看试题解析

二、第十八题

8. 双减政策实施后，学校为了解八年级学生每日完成书面作业所需时长x（单位：小时）的情况，在全校范围内随机抽取了八年级若干名学生进行调查，并将所收集的数据分组整理，绘制了如下两幅不完整的统计图表，请根据图表信息解答下列问题．

八年级学生每日完成书面作业所需时长情况的统计表

组别	所需时长（小时）	学生人数（人）
A	$0 < x \leq 0.5$	15
B	$0.5 < x \leq 1$	m
C	$1 < x \leq 1.5$	n
D	$1.5 < x \leq 2$	5

八年级学生每日完成书面作业所需时长情况的扇形统计图

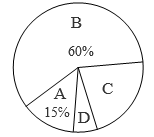(1)、求统计表中m，n的值．

(2)、已知该校八年级学生有800人，试估计该校八年级学生中每日完成书面作业所需时长满足

0.5 < x \leq 1.5

的共有多少人．

查看试题解析

9. 2022年末，中国迎来第一波疫情高峰．为加强同学们的防护意识，某校举行了以“疫情防护”为主题的知识竞赛活动．发现该校全体学生的竞赛成绩（百分制）均不低于60分，现从中随机抽取n名学生的竞赛成绩进行整理和分析（成绩得分用x表示，共分成四组），并绘制成如下的竞赛成绩分组统计表和扇形统计图，下面为部分数据：其中“ $80 \leq x < 90$ ”这组的部分数据（从小到大排序）如下：80，82，82，83，83，84，85，85，85，86，87，87，87，88，88……其中“ $90 \leq x \leq 100$ ”这组的数据如下：90，92，93，95，95，96，96，96，97，100．
竞赛成绩分组统计表
组别
竞赛成绩分组
频数
平均分
1
$60 \leq x < 70$
8
65
2
$70 \leq x < 80$
a
75
3
$80 \leq x < 90$
b
88
4
$90 \leq x \leq 100$
10
95
根据以上信息，回答下列问题：

(1)、下列说法正确的是____．

A、样本为n名学生 B、a＝12 C、m＝40

(2)、“ $90 \leq x \leq 100$ ”这组的数据的众数是．

(3)、随机抽取的这n名学生竞赛成绩的中位数是；平均分是；

(4)、若学生竞赛成绩达到96分以上（含96分）获奖，请你估计全校1200名学生中获奖的人数．

查看试题解析
10. 在体育活动课中，体育老师随机抽取了九年级甲、乙两班部分学生进行某体育项目的测试，并对成绩进行统计分析，绘制了频数分布表，请你根据表中的信息完成下列问题：
分组
频数
频率
第一组（不及格）
3
0.15
第二组（中）
b
0.20
第三组（良）
7
0.35
第四组（优）
6
a

(1)、频数分布表中 $a =$ ， $b =$ ；

(2)、如果该校九年级共有学生900人，估计该校该体育项目的成绩为良和优的学生有多少人？

(3)、已知第一组中有两个甲班学生，第二组中只有一个乙班学生，老师随机从这两个组中各选一名学生对体育活动课提出建议，则所选两人正好是甲班和乙班各一人的概率是多少？

查看试题解析

11. 针对新型冠状病毒事件，九（1）班全体学生参加学校举行的“珍惜生命，远离病毒”知识竞赛后，班长对本班成绩进行分析，制作如下的频数分布表和频数分布条形统计图

(

未完成

) .

除了60到70之间学生成绩尚未统计，还有6名学生成绩如下：90，96，98，99，99，99班长根据情况画出的扇形统计图如下：

类别	分数段	频数 $($ 人数 $)$
$A$	$60 \leq x < 70$	$a$
$B$	$70 \leq x < 80$	16
$C$	$80 \leq x < 90$	24
$D$	$90 \leq x < 100$	$b$

(1)、九（1）班有多少名学生？

(2)、求出

a

、

b

的值？并请补全条形统计图.

(3)、全校共有720名学生参加初赛，估计该校成绩

90 \leq x < 100

范围内的学生有多少人？

(4)、九（1）班甲、乙、丙三位同学的成绩并列第一，现选两人参加决赛，求恰好选中甲，乙两位同学的概率.

查看试题解析

12. 某校为了了解七年级800名学生跳绳情况，从七年级学生中随机抽取部分学生进行1分钟跳绳测试，并对测试成绩进行统计分析，得到如下所示的频数分布表：
跳绳个数 $(n)$
$0 < n \leq 100$
$100 < n \leq 120$
$120 < n \leq 140$
$140 < n \leq 160$
$160 < n \leq 200$
频数
16
30
50
$a$
24
所占百分比
8%
15%
25%
40%
$b$
请根据尚未完成的表格，解答下列问题：

(1)、本次随机抽取了名学生进行1分钟跳绳测试，表中a= ， b=；

(2)、补全频数直方图；

(3)、若绘制“七年级学生1分钟跳绳测试成绩扇形统计图”，则测试成绩在 $120 < n \leq 140$ 个所对应扇形的圆心角的度数是；

(4)、若跳绳个数超过140个为优秀，则该校七年级学生1分钟跳绳成绩优秀的约有多少人？

查看试题解析
13. 为了有效落实“双减”政策，某校随机抽取部分学生，开展了“书面作业完成时间”问卷调查．根据调查结果，绘制了如下不完整的统计图表：
频数分布统计表
组别
时间 $x （$ 分钟 $）$
频数
$A$
$0 \leq x < 20$
6
$B$
$20 \leq x < 40$
14
$C$
$40 \leq x < 60$
$m$
$D$
$60 \leq x < 80$
$n$
$E$
$80 \leq x < 100$
4
根据统计图表提供的信息解答下列问题：

(1)、频数分布统计表中的 $m =$ ▲ ， $n =$ ▲ ；并补全频数分布直方图；

(2)、已知该校有1000名学生，估计书面作业完成时间在60分钟以上(含60分钟)的学生有多少人？

(3)、若 $E$ 组有两名男同学、两名女同学，从中随机抽取两名学生了解情况，请用列表或画树状图的方法，求出抽取的两名同学恰好是一男一女的概率．

查看试题解析

14. 为庆祝中国共产党建党100周年，某校开展了党史知识竞赛．某年级随机选出了一个班的初赛成绩进行统计，得到如下统计图表，已知在扇形统计图

D

分数段对应的扇形六圆心角为

72 °

．某校组织读书征文比赛活动，评选出一、二、三等奖若干名，并绘成如图所示的统计表和扇形统计图（不完整），请你根据图中信息解答下列问题：

统计表

分段	成绩范围（分）	频数	频率
$A$	90~100	$a$	0.1
$B$	80~89	20	$b$
$C$	70~79	$c$	0.3
$D$	70分以下	10	$m$

注：90~100表示成绩 $x$ ，满足 $90 \leq x \leq 100$ ，以下相同．

扇形统计图

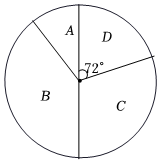(1)、在统计表中，

a =

，

b =

，

c =

；

(2)、若该年级参加初赛的学生共有2000人，根据以上统计数据估计该年级成绩在90分及以上的学生人数；

(3)、若统计表

A

分数段的男生比女生少1人，从

A

段中任选2人参加复赛，请用列表法或画树状图的方法，求出恰好抽到1名男生和1名女生的概率．

查看试题解析

三、第十九题

15. 一个深为6米的水池积存着少量水，现在打开水阀进水，下表记录了2小时内5个时刻的水位高度，其中x表示进水用时（单位：小时），y表示水位高度（单位：米）．

x

0

0.5

1

1.5

2

y

1

1.5

2

2.5

3

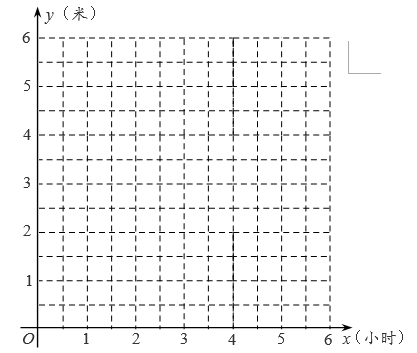为了描述水池水位高度与进水用时的关系，现有以下三种函数模型供选择： $y = k x + b$ （ $k \neq 0$ ），y=ax²+bx+c ( $a \neq 0$ )， $y = \frac{k}{x}$ （ $k \neq 0$ ）．

(1)、在平面直角坐标系中描出表中数据对应的点，再选出最符合实际的函数模型，求出相应的函数表达式，并画出这个函数的图象．

(2)、当水位高度达到5米时，求进水用时x．

查看试题解析
16. 某太阳能热水器水箱的最大蓄水量为160升，在没有放水的情况下匀速注水.已知水箱的蓄水量y（升）与注水时间x（分）

x（分）

0

4

8

12

……

y（升）

20

60

100

140

……

(1)、通过描点法判断变量x，y是否满足或近似地满足一次函数关系式.如果是，求y关于x的函数表达式.

(2)、按上述速度注满水箱，需要多少分钟？

查看试题解析
17. 习近平总书记在全国劳动模范和先进工作者表彰大会上讲话：劳动教育应纳入人才培养全过程.为了落实劳动教育，某学校邀请农科院专家指导学生进行小番茄的种植，经过试验，发现其平均单株产量 $y$ 千克与每平方米种植的株数 $x (2 \leq x \leq 8$ ，且 $x$ 为整数 $)$ 构成一种函数关系；每平方米种植2株时，平均单株产量为5千克；以同样的栽培条件，每平方米种植的株数每增加1株，单株产量将减少0.5千克.

(1)、求 $y$ 关于 $x$ 的函数表达式；

(2)、每平方米种植多少株时，能获得最大的产量？最大产量为多少千克？

查看试题解析
18. 某超市经销一种销售成本为每件40元的商品，据市场调查分析，如果按每件50元销售，一周能售出500件，若销售单价每涨1元，每周销量就减少10件，设销售单价为x元（ $x > 50$ ），一周的销售量为y件．

(1)、写出y与x的函数关系式：（标明x的取值范围）；

(2)、设一周的销售利润为S，写出S与x的函数关系式，并确定当单价是多少时利润最大；

(3)、在超市对该种商品投入不超过12000元的情况下，使得一周销售利润为8000元，销售单价应定为多少元？

查看试题解析
19. 小明、小亮利用遥控器在电子屏上分别玩甲、乙两个小飞机，甲、乙两个小飞机分别从水平线起点和距水平线起点高15m处同时出发，匀速上升60min．如图是甲、乙两个小飞机所在位置的高度y（单位：m）与飞机上升时间x（单位：min）的函数图象．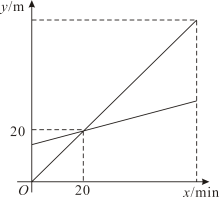

(1)、求这两个小飞机在上升过程中y关于x的函数解析式；

(2)、当这两个小飞机的高度相差18m时，求上升的时间．

查看试题解析
20. 甲、乙两车分别从相距360km的富区、哈市两地出发，匀速行驶，先相向而行，乙车在甲车出发1h后出发，到达富区后停止行驶，甲车到达哈市后，立即按原路原速返回富区（甲车调头的时间忽略不计），甲、乙两车距哈市的路程 $y_{1}$ （单位：km）， $y_{2}$ （单位：km）与甲车出发时间x（单位：h）之间的函数图象如图所示，请结合图象信息解答下列问题：

(1)、乙车的行驶速度是， $a =$ ；乙车距哈市的路程 $y_{2}$ 与甲车出发时间x之间的函数解析式是（不写自变量的取值范围）

(2)、甲车与乙车第一次相遇时，距离富区的路程是多少千米？

(3)、甲车出发多少小时后两车相距为100km？请直接写出答案．

查看试题解析

21. 某中学为筹备校庆，准备印制一批纪念册.该纪念册每册需要10张纸，其中4张彩色页，6张黑白页.印刷该纪念册的总费用由制版费和印刷费两部分组成，制版费与印数无关，价格为2200元，印刷费与印数的关系见表.

印数a（千册）	$0 ⩽ a < 5$	$a ⩾ 5$
彩色（元/张）	2.1	2
黑白（元/张）	0.8	0.5

(1)、若印制2千册，则共需多少元？

(2)、该校先印制了x千册纪念册，后发现统计失误，补印了y（

y ⩾ 5

）千册纪念册，且补印时无需再次缴纳制版费，学校发现补印的单册造价便宜了，但两次缴纳费用恰好相同.

①用含x的代数式表示y.

②若该校没有统计错误，一次性打印全部纪念册，最少需要多少钱？

查看试题解析

四、第二十题

22. 圭表（如图1）是我国古代一种通过测量正午日影长度来推定节气的天文仪器，它包括一根直立的标竿（称为“表”）和一把呈南北方向水平固定摆放的与标竿垂直的长尺（称为“圭”），当正午太阳照射在表上时，日影便会投影在圭面上，圭面上日影长度最长的那一天定为冬至，日影长度最短的那一天定为夏至.图2是一个根据某市地理位置设计的圭表平面示意图，表 AC垂直圭BC，已知该市冬至正午太阳高度角（即∠ABC）为37° ，夏至正午太阳高度角（即∠ADC）为84°，圭面上冬至线与夏至线之间的距离（即DB的长）为4米．

(1)、求∠BAD的度数．

(2)、求表AC的长（最后结果精确到0.1米）．
（参考数据：sin37°≈ $\frac{3}{5}$ ，cos37°≈ $\frac{4}{5}$ ，tan37°≈ $\frac{3}{4}$ ，tan84°≈ $\frac{19}{2}$ ）

查看试题解析
23. 如图1是一张折叠型方桌子，图2是其侧面结构示意图，支架 $A D$ 与 $C B$ 交于点O，测得 $A O = B O = 50 c m$ ， $C O = D O = 30 c m$ ．

(1)、若 $C D = 40 c m$ ，求 $A B$ 的长；

(2)、将桌子放平后，要使 $A B$ 距离地面的高为 $40 c m$ ，求两条桌腿需叉开角度 $∠ A O B$ ．

查看试题解析
24. 随着科学技术的不断进步，无人机被广泛应用到实际生活中，小星利用无人机来测量翡翠湖某处东西岸边 $B$ ， $C$ 两点之间的距离．如图所示，小星站在湖边的 $B$ 处遥控无人机，无人机在 $A$ 处距离地面的飞行高度是 $161.6 m$ ，此时从无人机测得岸边 $C$ 处的俯角为 $63 °$ ，他抬头仰视无人机时，仰角为 $α$ ，若小星的身高 $B E = 1.6 m$ ， $E A = 200 m$ （点 $A$ ， $E$ ， $B$ ， $C$ 在同一平面内）．

(1)、求仰角 $α$ 的正弦值；

(2)、求 $B$ ， $C$ 两点之间的距离（结果精确到 $1 m$ ）．（ $s i n 63 ° \approx 0.89$ ， $c o s 63 ° \approx 0.45$ ， $t a n 63 ° \approx 1.96$ ， $s i n 27 ° \approx 0.45$ ， $c o s 27 ° \approx 0.89$ ， $t a n 27 ° \approx 0.51$ ）

查看试题解析
25. 如图，梯形 $A B C D$ 是某水坝的横截面示意图，其中 $A B = C D$ ，坝顶 $B C = 2 m$ ，坝高 $C H = 5 m$ ，迎水坡 $A B$ 的坡度为 $i = 1 ： 1$ .

(1)、求坝底 $A D$ 的长；

(2)、为了提高堤坝防洪抗洪能力，防汛指挥部决定在背水坡加固该堤坝，要求坝顶加宽 $0.5 m$ ，背水坡坡角改为 $α = 30 °$ .求加固总长5千米的堤坝共需多少土方？（参考数据： $π \approx 3.14 ， \sqrt{2} \approx 1.41 ， \sqrt{3} \approx 1.73$ ；结果精确到 $0.1 m^{3}$ ）

查看试题解析
26. 图1是某型号挖掘机，该挖掘机是由基座、主臂和伸展臂构成．图2是某种工作状态下的侧面结构示意图（ $M N$ 是基座的高， $M P$ 是主臂， $P Q$ 是伸展臂， $E M ∥ Q N$ ）．已知基座高度 $M N$ 为 $1 m$ ，主臂 $M P$ 长为 $5 m$ ，测得主臂伸展角 $∠ P M E = 37 °$ ．
（参考数据： $s i n 37 ° \approx \frac{3}{5} ， t a n 37 ° \approx \frac{3}{4} ， s i n 53 ° \approx \frac{4}{5} ， t a n 53 ° \approx \frac{4}{3}$ ）

(1)、求点P到地面的高度；

(2)、若挖掘机能挖的最远处点Q到点N的距离为 $7 m$ ，求 $∠ Q P M$ 的度数．

查看试题解析
27. 如图，是一个放置于水平桌面的平板支架的示意图，底座的高 $A B$ 为 $5 c m$ ，宽 $M N$ 为 $10 c m$ ，点A是 $M N$ 的中点，连杆 $B C 、 C D$ 的长度分别为 $18.5 c m$ 和 $15 c m$ ， $∠ C B A = 150 °$ ，且连杆 $B C 、 C D$ 与 $A B$ 始终在同一平面内．

(1)、求点C到水平桌面的距离；

(2)、产品说明书提示，若点D与A的水平距离超过 $A N$ 的长度，则该支架会倾倒．现将 $∠ D C B$ 调节为 $80 °$ ，此时支架会倾倒吗？（参考数据∶ $t a n 20 ° \approx 0.36 ， c o t 20 ° \approx 2.75 ， s i n 20 ° \approx 0.34 ， c o s 20 ° \approx 0.94$ ）

查看试题解析
28. 如图1，某学校开展“交通安全日”活动．在活动中，交警叔叔向同学们展示了大货车盲区的分布情况，并提醒大家：坐在驾驶室的司机根本看不到在盲区中的同学们，所以一定要远离大货车的盲区，保护自身安全．小刚所在的学习小组为了更好的分析大货车盲区的问题，将图1用平面图形进行表示，并标注了测量出的数据，如图2．在图2中大货车的形状为矩形，而盲区1为梯形，盲区2、盲区3为直角三角形，盲区4为正方形．

请你帮助小刚的学习小组解决下面的问题：

(1)、盲区1的面积约是m²；盲区2的面积约是m²；（ $\sqrt{2}$ ≈1.4， $\sqrt{3}$ ≈1.7，sin25°≈0.4，cos25°≈0.9，tan25°≈0.5，结果保留整数）

(2)、如果以大货车的中心A点为圆心，覆盖所有盲区的半径最小的圆为大货车的危险区域，请在图2中画出大货车的危险区域．

查看试题解析

组别	竞赛成绩分组	频数	平均分
1	$60 \leq x < 70$	8	65
2	$70 \leq x < 80$	a	75
3	$80 \leq x < 90$	b	88
4	$90 \leq x \leq 100$	10	95

分组	频数	频率
第一组（不及格）	3	0.15
第二组（中）	b	0.20
第三组（良）	7	0.35
第四组（优）	6	a

跳绳个数 $(n)$	$0 < n \leq 100$	$100 < n \leq 120$	$120 < n \leq 140$	$140 < n \leq 160$	$160 < n \leq 200$
频数	16	30	50	$a$	24
所占百分比	8%	15%	25%	40%	$b$

组别	时间 $x （$ 分钟 $）$	频数
$A$	$0 \leq x < 20$	6
$B$	$20 \leq x < 40$	14
$C$	$40 \leq x < 60$	$m$
$D$	$60 \leq x < 80$	$n$
$E$	$80 \leq x < 100$	4

x（分）	0	4	8	12	……
y（升）	20	60	100	140	……