备考2023年中考数学绍兴卷变式阶梯训练:11-16题
试卷更新日期:2023-04-05 类型:三轮冲刺
一、第十一题
-
1. 分解因式:x2+x= .2. 分解因式:.3. 把分解因式得4. 分解因式: .5. 因式分解:2x(a-b)-6y(b-a)=.6. (2x-10)(x-2)-(x-2)(x-13)可分解因式为(x+a)(x+b),则的值是.7. 若m2=n+2020,n2=m+2020(m≠n),那么代数式m3﹣2mn+n3的值 .
二、第十二题
-
8. 关于x的不等式3x-2>x 的解是 .9. 不等式的解集为.10. 解不等式:的解集是 .11. 关于的一元一次不等式的解集为 , 则的值为.12. 若关于x的方程x-m=4的解满足不等式2x+1 >3,则可取的负整数为= .13. 已知不等式的正整数解恰好是1、2、3,则的取值范围是 .14. 对于实数x,y,我们定义符号min{x,y}的意义为:当x<y时,min{x,y}=x;当x≥y时,min{x,y}=y,如:min{6,﹣4}=﹣4,min{4,4}=4,min{ , }时,则x的取值范围为 .
三、第十三题
-
15. 元朝朱世杰的《算学启蒙》一书记载:“良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何追及之.” 其题意为:“良马每天行240里,劣马每天行150里,劣马先行12天,良马要几天追上劣马?”答:良马追上劣马需要的天数是 .16. 我国古代《孙子算经》记载了这样一个数学问题:“今有三人共车,二车空;二人共车,九人步.问车有几何?意思是”每3人共乘一辆车,最终剩余2辆车;每2人共乘一辆车,最终有9人无车可乘,则车有辆.17. 《孙子算经》是中国传统数学的重要著作之一,其中记载的“荡杯问题”很有趣.《孙子算经》记载“今有妇人河上荡杯.津吏问曰:‘杯何以多?’妇人曰:‘家有客.’津吏曰:‘客几何?’妇人曰:‘二人共饭,三人共羹,四人共肉,凡用杯七十八.’不知客几何?”译文:“人同吃一碗饭,人同吃一碗羹,人同吃一碗肉,共用个碗,问有多少客人?”,则客人的个数为.18. 清人徐子云《算法大成》中有一首名为“寺内僧多少”的诗:
巍巍古寺在山林,不知寺中几多僧.
三百六十四只碗,众僧刚好都用尽.
三人共食一碗饭,四人共吃一碗羹.
请问先生明算者,算来寺内几多僧.
诗的大意是:在巍巍的大山和茂密的森林之中,有一座千年古寺,寺中有364只碗,要是3个和尚共吃一碗饭,4个和尚共喝一碗粥,这些碗刚好用完,问寺内有多少和尚?设有和尚人,由题意可列方程为 .
 19. 明代数学家吴敬所著的《九章自述比类大全》中有一首数学诗叫“宝塔装灯”,内容为“远望巍巍塔七层,红灯点点倍加增,共灯三百八十一,请问顶层几盏灯?”大致意思是有一座七层高塔,从底层开始,每层安装的灯的数目都是上一层的2倍,请你算出塔的顶层有盏灯.20. 中国古代重要的数学著作《孙子算经》中有这样一个问题:“今有妇人河上荡杯,津吏问曰:杯何以多?妇人曰:家有客.津吏曰:客几何?妇人曰:二人共饭,三人共羹,四人共肉,凡用杯六十五,不知客几何?”其大意为:一位妇人在河边洗碗.津吏问道:“为什么要洗这么多碗?”妇人回答:“家里来客人了”津吏问:“有多少客人?”妇人回答:“每二人合用一只饭碗,每三人合用一只汤碗,每四人合用一只肉碗,共用65只碗.”来了多少位客人.根据题意,妇人家中访客的人数是人.21. 《九章算术》是中国古代张苍、耿寿昌所撰写的一部数学专著 .是《算经十书》中最重要的一部,成于公元一世纪左右 .全书总结了战国、秦、汉时期的数学成就 .同时,《九章算术》在数学上还有其独到的成就,不仅最早提到分数问题,也首先记录了盈不足等问题,其中有一个数学问题“今有垣厚一丈,两鼠对穿 .大鼠日一尺,小鼠亦一尺 .大鼠日自倍,小鼠日自半 .问:何日相逢?”.译文:“有一堵一丈(旧制长度单位,1丈=10尺=100寸)厚的墙,两只老鼠从两边向中间打洞 .大老鼠第一天打一尺,小老鼠也是一尺 .大老鼠每天的打洞进度是前一天的一倍,小老鼠每天的进度是前一天的一半 .问它们几天可以相逢?”请你用所学数学知识方法给出答案: .
19. 明代数学家吴敬所著的《九章自述比类大全》中有一首数学诗叫“宝塔装灯”,内容为“远望巍巍塔七层,红灯点点倍加增,共灯三百八十一,请问顶层几盏灯?”大致意思是有一座七层高塔,从底层开始,每层安装的灯的数目都是上一层的2倍,请你算出塔的顶层有盏灯.20. 中国古代重要的数学著作《孙子算经》中有这样一个问题:“今有妇人河上荡杯,津吏问曰:杯何以多?妇人曰:家有客.津吏曰:客几何?妇人曰:二人共饭,三人共羹,四人共肉,凡用杯六十五,不知客几何?”其大意为:一位妇人在河边洗碗.津吏问道:“为什么要洗这么多碗?”妇人回答:“家里来客人了”津吏问:“有多少客人?”妇人回答:“每二人合用一只饭碗,每三人合用一只汤碗,每四人合用一只肉碗,共用65只碗.”来了多少位客人.根据题意,妇人家中访客的人数是人.21. 《九章算术》是中国古代张苍、耿寿昌所撰写的一部数学专著 .是《算经十书》中最重要的一部,成于公元一世纪左右 .全书总结了战国、秦、汉时期的数学成就 .同时,《九章算术》在数学上还有其独到的成就,不仅最早提到分数问题,也首先记录了盈不足等问题,其中有一个数学问题“今有垣厚一丈,两鼠对穿 .大鼠日一尺,小鼠亦一尺 .大鼠日自倍,小鼠日自半 .问:何日相逢?”.译文:“有一堵一丈(旧制长度单位,1丈=10尺=100寸)厚的墙,两只老鼠从两边向中间打洞 .大老鼠第一天打一尺,小老鼠也是一尺 .大老鼠每天的打洞进度是前一天的一倍,小老鼠每天的进度是前一天的一半 .问它们几天可以相逢?”请你用所学数学知识方法给出答案: .四、第十四题
-
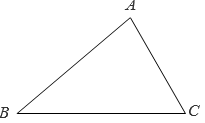
22. 如图,在△ABC 中, ∠ABC=40°, ∠BAC=80°,以点 A为圆心, AC 长为半径作弧,交射线 BA 于点 D,连结 CD ,则 ∠BCD 的度数是 .
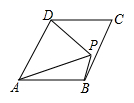
 23. 如图,D是内部的一点, , . 下列结论:①;②;③;④平分 . 其中结论正确的序号是( )
23. 如图,D是内部的一点, , . 下列结论:①;②;③;④平分 . 其中结论正确的序号是( ) A、①②③ B、①②④ C、①③④ D、②③④24. 如图,D为内一点,平分 , , , 若 , . 则的长为( )
A、①②③ B、①②④ C、①③④ D、②③④24. 如图,D为内一点,平分 , , , 若 , . 则的长为( )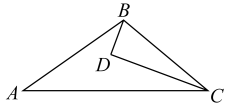 A、1 B、 C、2 D、25. 如图,在中, , , 平分 , , 为边的垂直平分线且分别交、于点、 , 若 , , 则的长是( )
A、1 B、 C、2 D、25. 如图,在中, , , 平分 , , 为边的垂直平分线且分别交、于点、 , 若 , , 则的长是( )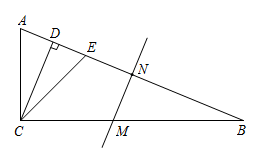 A、2 B、 C、 D、26. 如图,在中,根据规作图痕迹,下列说法不一定正确的是( ).
A、2 B、 C、 D、26. 如图,在中,根据规作图痕迹,下列说法不一定正确的是( ).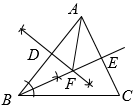 A、 B、 C、 D、27. 如图,等腰中, , , 于点 , 的平分线分别交、于、两点,为的中点,的延长线交于点 , 连接 , 下列结论:;为等腰三角形;;; , 其中正确结论有( )
A、 B、 C、 D、27. 如图,等腰中, , , 于点 , 的平分线分别交、于、两点,为的中点,的延长线交于点 , 连接 , 下列结论:;为等腰三角形;;; , 其中正确结论有( )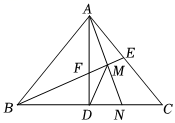 A、2个 B、3个 C、4个 D、5个28. 如图,在和中, , , , 点M、N、P分别为的中点,若绕点A在平面内自由旋转,则面积最大时的值为( )
A、2个 B、3个 C、4个 D、5个28. 如图,在和中, , , , 点M、N、P分别为的中点,若绕点A在平面内自由旋转,则面积最大时的值为( )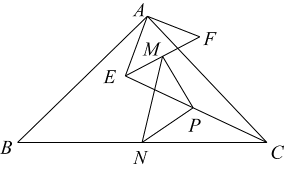 A、 B、 C、 D、16
A、 B、 C、 D、16五、第十五题
-
29. 如图,在平面直角坐标系xOy中,点 A (0,4), B(3,4),将△ABO向右平移到 △CDE 位置, A 的对应点是 C, O的对应点是 E,函数 的图象经过点 C 和DE的中点 F,则k的值是 .
 30. 如图,在平面直角坐标系中,点A在第一象限,轴于点B,反比例函数( , )的图象与线段AB交于点C,且.若的面积为12,则k的值为.
30. 如图,在平面直角坐标系中,点A在第一象限,轴于点B,反比例函数( , )的图象与线段AB交于点C,且.若的面积为12,则k的值为.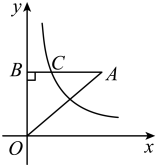 31. 如图是反比例函数和在第一象限的图像,直线轴,并分别交两条双曲线于、两点,若 , 则.
31. 如图是反比例函数和在第一象限的图像,直线轴,并分别交两条双曲线于、两点,若 , 则.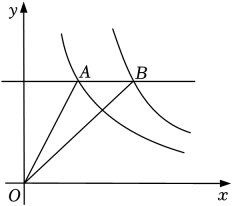 32. 如图,在平面直角坐标系中,的顶点、在轴上,、两点分别在反比例函数与的图像上,若的面积为4,则的值为 .
32. 如图,在平面直角坐标系中,的顶点、在轴上,、两点分别在反比例函数与的图像上,若的面积为4,则的值为 .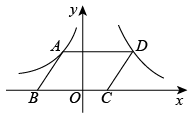 33. 如图,正方形OABC的顶点A、C分别在x轴和y轴上,E、F分别是边AB、OA上的点,且∠ECF=45°,将△ECF沿着CF翻折,点E落在x轴上的点D处.已知反比例函数y1=和y2=分别经过点B、点E,若S△COD=5,则k1﹣k2= .
33. 如图,正方形OABC的顶点A、C分别在x轴和y轴上,E、F分别是边AB、OA上的点,且∠ECF=45°,将△ECF沿着CF翻折,点E落在x轴上的点D处.已知反比例函数y1=和y2=分别经过点B、点E,若S△COD=5,则k1﹣k2= .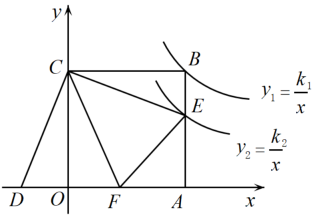 34. 如图,B、C分别是反比例函数与的图象上的点,且轴,过点C作BC的垂线交于y轴于点A,则的面积为.
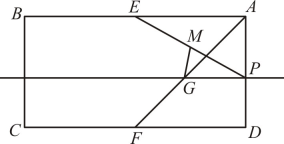
34. 如图,B、C分别是反比例函数与的图象上的点,且轴,过点C作BC的垂线交于y轴于点A,则的面积为.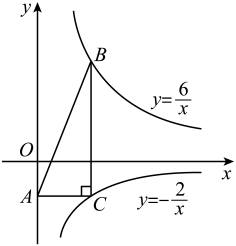 35. 如图,在平行四边形OABC中,点B在反比例函数y=(x>0)上,延长OC至点E,使得到OC=2CE,点D是直线BC与y轴的交点,过点D作DF∥AB交射线AE于点F,连结OF,则△OAF的面积为.
35. 如图,在平行四边形OABC中,点B在反比例函数y=(x>0)上,延长OC至点E,使得到OC=2CE,点D是直线BC与y轴的交点,过点D作DF∥AB交射线AE于点F,连结OF,则△OAF的面积为.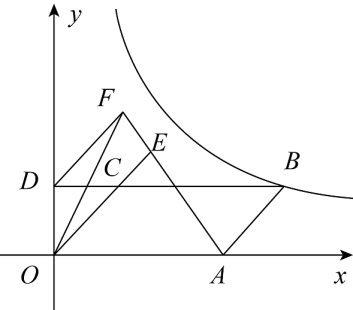
六、第十六题
-
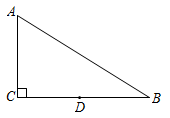
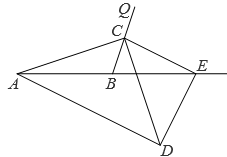
36. 如图, AB=10,点C在射线BQ上的动点,连结AC,作CD⊥AC, CD=AC ,动点E在AB 延长线上, tan∠QBE=3,连结 CE, DE ,当CE=DE, CE⊥DE时, BE 的长是 .
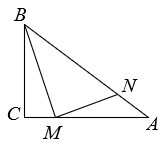
 37. 如图,在△ABC中,DC平分∠ACB,于点D, , 若 , , 则tan∠CBD的值为.
37. 如图,在△ABC中,DC平分∠ACB,于点D, , 若 , , 则tan∠CBD的值为.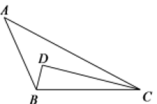 38. 如图,在中,弦 , 点为圆周上一动点,连接、 , 为上一点,且 , , 则周长的最大值为.
38. 如图,在中,弦 , 点为圆周上一动点,连接、 , 为上一点,且 , , 则周长的最大值为.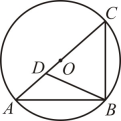 39. 如图,在中, , .D是边BC的中点,点E在AB边上,将沿直线DE翻折,使点B落在同一平面内点F处,线段FD交边AB于点G,若时,则.
39. 如图,在中, , .D是边BC的中点,点E在AB边上,将沿直线DE翻折,使点B落在同一平面内点F处,线段FD交边AB于点G,若时,则.