备考2023年中考数学绍兴卷变式阶梯训练:6-10题
试卷更新日期:2023-04-05 类型:三轮冲刺
一、第六题
-
1. 如图,把一块三角板 ABC 的直角顶点B放在直线 EF 上, ∠C=30° ,AC∥EF,则 ∠1= ( )
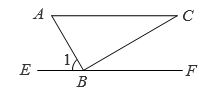 A、30° B、45° C、60° D、75°2. 如图所示,将三角尺的直角顶点放在直尺的一边上, , , 则的度数为( )
A、30° B、45° C、60° D、75°2. 如图所示,将三角尺的直角顶点放在直尺的一边上, , , 则的度数为( )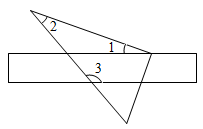 A、 B、 C、 D、3. 如图,直线ab,点A在直线a上.在ABC中,∠B=90°,∠C=25°,∠1=75°,则∠2的度数为( )
A、 B、 C、 D、3. 如图,直线ab,点A在直线a上.在ABC中,∠B=90°,∠C=25°,∠1=75°,则∠2的度数为( ) A、30° B、35° C、40° D、65°4. 直线BD∥EF,两个直角三角板如图摆放,若∠CBD=10°,则∠1=( )
A、30° B、35° C、40° D、65°4. 直线BD∥EF,两个直角三角板如图摆放,若∠CBD=10°,则∠1=( )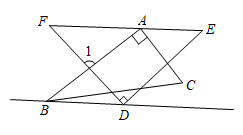 A、75° B、80° C、85° D、95°5. 如图,将一块含有45°角的直角三角板放置在两条平行线上,若∠1=25°,则∠2为( )
A、75° B、80° C、85° D、95°5. 如图,将一块含有45°角的直角三角板放置在两条平行线上,若∠1=25°,则∠2为( ) A、15° B、20° C、25° D、30°6. 将一副直角三角板按如图所示方式叠放,现将含30°角的三角板固定不动,把含45°角的三角板绕O点按每秒15°的速度沿逆时针方向匀速旋转一周,当两块三角板的斜边平行时,则三角板旋转的时间为( )秒.
A、15° B、20° C、25° D、30°6. 将一副直角三角板按如图所示方式叠放,现将含30°角的三角板固定不动,把含45°角的三角板绕O点按每秒15°的速度沿逆时针方向匀速旋转一周,当两块三角板的斜边平行时,则三角板旋转的时间为( )秒. A、5 B、7 C、5或17 D、7或197. 将一副三角板按如图放置,有下列结论:①若∠2=30°,则AC∥DE;
A、5 B、7 C、5或17 D、7或197. 将一副三角板按如图放置,有下列结论:①若∠2=30°,则AC∥DE;②∠BAE+∠CAD=180°;③若BC∥AD,则∠2=30°;④若∠CAD=150°,则
∠4=∠C.其中正确的是( )
 A、①②④ B、①③④ C、②③④ D、①②③④
A、①②④ B、①③④ C、②③④ D、①②③④二、第七题
-
8. 已知抛物线 y=x2+mx的对称轴为直线 x=2 ,则关于x的方程 x2+mx=5的根是( )A、0,4 B、1,5 C、1,-5 D、-1,59. 如图是二次函数的部分图象,则关于的一元二次方程的解是( )
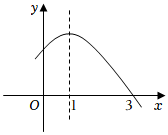 A、 , B、 , C、 , D、 ,10. 二次函数的图像经过点 , , 则关于x的方程的根是( )A、 , B、 , C、 , D、 ,11. 二次函数y=x2+bx的对称轴为x=1,若关于一元二次方程x2+bx-t=0(t为实数)在-1<x<4的范围内有解,则t的取值范围是( )A、t<8 B、t<3 C、-1≤t<3 D、-1≤t<812. 三个方程的正根分别记为 , 则下列判断正确的是( )A、 B、 C、 D、13. 若二次函数y=ax2+bx-1的最小值为-3,则方程|ax2+bx-1|=2的不相同实数根的个数是( )A、2 B、3 C、4 D、514. “如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m,n(m<n)是关于x的方程1﹣(x﹣p)(x﹣q)=0的两个根,且p<q,则p,q,m,n的大小关系是( )A、m<p<q<n B、p<m<n<q C、m<p<n<q D、p<m<q<n
A、 , B、 , C、 , D、 ,10. 二次函数的图像经过点 , , 则关于x的方程的根是( )A、 , B、 , C、 , D、 ,11. 二次函数y=x2+bx的对称轴为x=1,若关于一元二次方程x2+bx-t=0(t为实数)在-1<x<4的范围内有解,则t的取值范围是( )A、t<8 B、t<3 C、-1≤t<3 D、-1≤t<812. 三个方程的正根分别记为 , 则下列判断正确的是( )A、 B、 C、 D、13. 若二次函数y=ax2+bx-1的最小值为-3,则方程|ax2+bx-1|=2的不相同实数根的个数是( )A、2 B、3 C、4 D、514. “如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m,n(m<n)是关于x的方程1﹣(x﹣p)(x﹣q)=0的两个根,且p<q,则p,q,m,n的大小关系是( )A、m<p<q<n B、p<m<n<q C、m<p<n<q D、p<m<q<n三、第八题
-
15. 如图,在平行四边形 中, , , , 是对角线 上的动点,且 , , 分别是边 ,边 上的动点.下列四种说法:
①存在无数个平行四边形 ;
②存在无数个矩形 ;
③存在无数个菱形 ;
④存在无数个正方形 .其中正确的个数是( )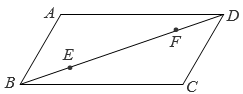 A、1 B、2 C、3 D、416. 如图,四边形是平行四边形,添加下列条件,能判定这个四边形是矩形的是( )
A、1 B、2 C、3 D、416. 如图,四边形是平行四边形,添加下列条件,能判定这个四边形是矩形的是( )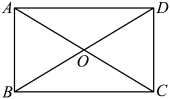 A、 B、 C、 D、17. 如图,已知四边形ABCD的对角线AC、BD相交于点O,则下列能判断它是正方形的条件是( )
A、 B、 C、 D、17. 如图,已知四边形ABCD的对角线AC、BD相交于点O,则下列能判断它是正方形的条件是( ) A、AC=BC=CD=DA B、AO=BO=CO=DO,AC⊥BD C、AO=CO,BO=DO,AC⊥BD D、AB=BC,CD⊥DA18. 如图,点E,F,G,H分别为四边形ABCD的边AB,BC,CD,DA的中点.下列三种说法:
A、AC=BC=CD=DA B、AO=BO=CO=DO,AC⊥BD C、AO=CO,BO=DO,AC⊥BD D、AB=BC,CD⊥DA18. 如图,点E,F,G,H分别为四边形ABCD的边AB,BC,CD,DA的中点.下列三种说法:
① .四边形EFGH一定是平行四边形;
②.若AC=BD,则四边形EFGH 是菱形;
③.若AC⊥BD,则四边形EFGH是矩形.
其中正确的是( )
A、① B、①② C、①③ D、①②③19. 如图,在中,点、、分别为边、、的中点,分别联结、、、 , 点是与的交点,下列结论中,正确的个数是( )
的周长是周长的一半;与互相平分;③如果 , 那么点到四边形四个顶点的距离相等;④如果 , 那么点到四边形四条边的距离相等.
A、1个 B、2个 C、3个 D、4个20. 如图,正方形 中,点P为 延长线上任一点,连结 ,过点P作 ,交 的延长线于点E,过点E作 于点F.下列结论:① ;② ;③ ;④若 ,则 .其中正确的个数为( ) A、1 B、2 C、3 D、421. 如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连接EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( )
A、1 B、2 C、3 D、421. 如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连接EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个四、第九题
-
22. 已知 (x1 , x2),(x2 , y2),(x3 , y3)为直线 y=-2x+3 上的三个点,且x1< x2< x3 , 则以下判断正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则23. 点 、 在直线 上,若 ,则 与 大小关系是( )
A、 B、 C、 D、无法确定24. 已知(-3,y1) (-1,y2),( , y3)是直线y=x+2上的三个点,则y1 , y2 , y3的大小关系是( )A、y1>y2>y3 B、y3>y2>y1 C、y1>y3>y2 D、y3>y1>y225. 若一次函数的图象经过点和点 , 当时, , 则m的取值范围是( )A、 B、 C、 D、26. 记实数x1 , x2 , …,xn中的最大数为max{x1 , x2 , …,xn},例如max{﹣2,0,2}=2,则函数y=max{﹣3x﹣3,2﹣x,x}的图象大致为( )A、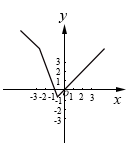 B、
B、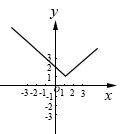 C、
C、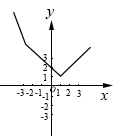 D、
D、 27. 在下列函数图象上任取不同的两点P(x1 , y1), Q(x2 , y2), 一定能使的是( )A、y=(x>0) B、y=-(x-2)2+5(x≥0) C、y=(x-3)2-4(x<0) D、y=3x+728. 若点 、 是一次函数 图象上不同的两点,记 ,当 时,a的取值范围是( )A、 B、 C、 D、
27. 在下列函数图象上任取不同的两点P(x1 , y1), Q(x2 , y2), 一定能使的是( )A、y=(x>0) B、y=-(x-2)2+5(x≥0) C、y=(x-3)2-4(x<0) D、y=3x+728. 若点 、 是一次函数 图象上不同的两点,记 ,当 时,a的取值范围是( )A、 B、 C、 D、五、第十题
-
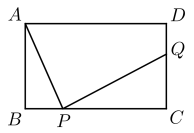
29. 将一张以AB为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角形相似),剩下的是如图所示的四边形纸片 ,其中 , , , , ,则剪掉的两个直角三角形的斜边长不可能是( )
 A、 B、 C、10 D、30. 九章算术记载“今有邑方不知大小,各中开门.出北门三十步有木,出西门七百五十步见木.问邑方有几何?”意思是:如图,点M、点N分别是正方形的边、的中点, , , 过点A,且步,步,则正方形的边长为( )
A、 B、 C、10 D、30. 九章算术记载“今有邑方不知大小,各中开门.出北门三十步有木,出西门七百五十步见木.问邑方有几何?”意思是:如图,点M、点N分别是正方形的边、的中点, , , 过点A,且步,步,则正方形的边长为( ) A、步 B、步 C、步 D、步31. 如图,在中,对角线 , 交于点 , 为三等分点且 , 连接交于点 , 若的面积为1,则的面积为( )
A、步 B、步 C、步 D、步31. 如图,在中,对角线 , 交于点 , 为三等分点且 , 连接交于点 , 若的面积为1,则的面积为( ) A、16 B、20 C、24 D、1832. 如图,在中,中线、相交于点F,连接 , 则下列结论:① , ② , ③ , ④ . 其中正确结论的个数是( )
A、16 B、20 C、24 D、1832. 如图,在中,中线、相交于点F,连接 , 则下列结论:① , ② , ③ , ④ . 其中正确结论的个数是( ) A、1个 B、2个 C、3个 D、4个33. 如图,已知 , 分别为正方形的边 , 的中点,与交于点.则下列结论:① , ② , ③ , ④.其中正确结论的有( )
A、1个 B、2个 C、3个 D、4个33. 如图,已知 , 分别为正方形的边 , 的中点,与交于点.则下列结论:① , ② , ③ , ④.其中正确结论的有( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个