2023年苏科版数学七年级下册全方位训练卷第十一章一元一次不等式（进阶版）

试卷更新日期：2023-04-05 类型：单元试卷

进入出卷网下载

一、单选题（每题2分，共16分）

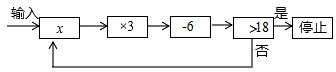
1. 已知a，b，c，d是实数，若 $a > b$ ， $c = d$ ，则（）

A、 $a + c > b + d$ B、 $a + b > c + d$ C、 $a + c > b - d$ D、 $a + b > c - d$

查看试题解析
2. 若a，b，c，d为整数，且a＜2b，b＜3c，c＜4d，d＜100，则a可能取的最大值是（）

A、2367 B、2375 C、2391 D、2399

查看试题解析
3. 关于 $x$ 的不等式 $(m + 1) x \geq m + 1$ ，下列说法正确的是（）

A、解集为 $x \geq 1$ B、解集为 $x \leq 1$ C、解集为 $x$ 取任何实数 D、无论 $m$ 取何值，不等式肯定有解

查看试题解析
4. 下列说法错误的是（）

A、由 $a > b$ ，得 $b < a$ B、由 $- \frac{1}{2} x < y$ 得 $x > - 2 y$ C、不等式 $x \leq 9$ 的解一定是不等式 $x < 10$ 的解 D、若 $a > b$ ，则 $a c^{2} > b c^{2}$ （c为有理数）

查看试题解析
5. 设 $x_{1}$ ， $x_{2}$ ， $x_{3}$ 都是小于－1的数，且 $a_{1} > a_{2} > a_{3} > 0$ ，若满足 $a_{1} (x_{1} + 1) (x_{1} - 2) = 1$ ， $a_{2} (x_{2} + 1) (x_{2} - 2) = 2$ ， $a_{3} (x_{3} + 1) (x_{3} - 2) = 3$ ，则必有（）

A、 $x_{1} > x_{2} > x_{3}$ B、 $x_{1} = x_{2} = x_{3}$ C、 $x_{1} < x_{2} < x_{3}$ D、不能确定 $x_{1}$ ， $x_{2}$ ， $x_{3}$ 的大小关系

查看试题解析
6. 如果关于 $x$ 的不等式组 ${\begin{array}{l} \frac{x - m}{3} \leq 1 \\ x - 4 > 3 (x - 2) \end{array}$ 的解集为 $x < 1$ ，且关于 $x$ 的分式方程 $\frac{2}{1 - x} + \frac{mx}{x - 1} = 3$ 有非负数解，则所有符合条件的整数 $m$ 的值之和是（）

A、-2 B、0 C、3 D、5

查看试题解析
7. 运行程序如图所示，从“输入实数 x”到“结果是否＜18”为一次程序操作，若输入 x 后程序操作仅进行了三次就停止，那么 x 的取值范围是（）

A、 $x \geq \frac{32}{9}$ B、 $\frac{32}{9} \leq x \leq \frac{14}{3}$ C、 $\frac{32}{9} < x \leq \frac{14}{3}$ D、 $x \leq \frac{14}{3}$

查看试题解析
8. 随着科技的进步，在很多城市都可以通过手机APP实时查看公交车到站情况.小聪同学想乘公交车，他走到A、B两站之间的C处，拿出手机查看了公交车到站情况，发现他与公交车的距离为700m（如图），此时他有两种选择：
①与公交车相向而行，到A公交站去乘车；
②与公交车同向而行，到B公交站去乘车.
假设公交车的速度是小聪速度的6倍，小聪无论选择哪站乘坐都不会错过这辆公交车，则A，B两公交站之间的距离最大为（）

A、240m B、260m C、280m D、300m

查看试题解析

二、填空题（每空3分，共18分）

9. 已知式子|x+1|+|x﹣2|+|y+3|+|y﹣4|＝10，则2x+y的最小值是．

查看试题解析
10. 已知关于 $x$ ， $y$ 的方程组 ${\begin{cases} a x + 3 y = 12 \\ x - 3 y = 0 \end{cases}$ 的解为整数，且关于 $x$ 的不等式组 ${\begin{cases} 2 (x + 1) < x + 5 \\ 3 x > a - 4 \end{cases}$ 有且仅有3个整数解，则所有满足条件的整数a的和为.

查看试题解析
11. 已知实数 $a$ ， $b$ ，满足 $1 \leq a + b \leq 4$ ， $0 \leq a - b \leq 1$ 且 $a - 2 b$ 有最大值，则 $8 a + 2021 b$ 的值是.

查看试题解析
12. 运行程序如图所示，规定：从“输入一个值 $x$ ”到“结果是否 $> 94$ ”为一次程序操作，如果程序操作进行了三次才停止，那么 $x$ 的取值范围是.

查看试题解析
13. 若x=3，y=b；x=a，y= $\frac{11}{2}$ 都是关于x，y的方程3x-2y=c的解，且3a-2b=2c²+2c-10，则关于x的不等式c²x-3a＞10x+2b的解集是．

查看试题解析
14. 若规定 $[m]$ 表示一个正实数的整数部分，例如： $[3.14] = 3$ ， $[\sqrt{2}] = 1$ ，则 $[5 - \sqrt{3}] =$ ．

查看试题解析
15. 已知关于x、y的方程组 ${\begin{matrix} x + 3 y = 2 a + 4 \\ 2 x - y = 1 - 3 a \end{matrix}$ 的解都为非负数，且满足 $2 a + b = 5$ ， $2 \leq b \leq 5$ ，若 $z = a - b$ ，则z的取值范围是

查看试题解析
16. 某工厂计划m天生产2160元个零件，若安排15名工人每人每天加工a个零件（a为整数）恰好完成.实际开工x天后，其中3人外出培训，剩下的工人每人每天多加工2个零件，不能按期完成这次任务，则a与m的数量关系是， a的值至少为

查看试题解析

三、解答题（共9题，共86分）

17. 解下列不等式组

(1)、 ${\begin{matrix} 2 x - 2 > \frac{1}{2} (x - 7) + 1 \\ \frac{2 x - 5}{3} + 3 < \frac{x}{5} + 2 \end{matrix}$

(2)、 ${\begin{matrix} 4 x + \frac{2}{3} < \frac{x - 8}{5} + 2 \\ 2 - \frac{x}{3} > 3 - \frac{x}{2} \end{matrix}$

(3)、 ${\begin{matrix} 1 < \frac{2 x - 5}{3} < 3 \\ (x - \frac{2}{3}) + 5 \geq 2 x - \frac{3}{2} \end{matrix}$

(4)、 ${\begin{matrix} \begin{matrix} x - 1 > - 3 \\ \frac{x}{2} - 1 < \frac{x}{3} \end{matrix} \\ 3 < 2 (x - 1) < 10 \end{matrix}$

(5)、 ${\begin{matrix} \begin{matrix} 2 x + 3 < 9 - x \\ 6 x - 1 < 5 \end{matrix} \\ 2 - x \leq 3 x + 7 \end{matrix}$

查看试题解析
18. 已知关于x ， y的方程满足方程组 ${\begin{array}{l} 3 x + 2 y = m + 1 ① \\ 2 x + y = m - 1 ② \end{array}$ ，
（Ⅰ）若 x-y=2 ，求m的值；

（Ⅱ）若x ， y ， m均为非负数，求m的取值范围，并化简式子 $| m - 3 | + | m - 5 |$ ；

（Ⅲ）在（Ⅱ）的条件下求 $s = 2 x - 3 y + m$ 的最小值及最大值．

查看试题解析
19. 一般的，数a的绝对值|a|表示数a对应的点与原点的距离．同理，绝对值|a﹣b|表示数轴上数a对应的点与数b对应的点的距离．例如：|3﹣0|指在数轴上表示数3的点与原点的距离，所以3的绝对值是3，即|3﹣0|＝|3|＝3．|6﹣2|指数轴上表示6的点和表示2的点的距离，所以数轴上表示6的点和表示2的点的距离是4，即|6﹣2|＝4．
结合数轴与绝对值的知识解答下列问题：

(1)、解含绝对值的方程|x+2|＝1得x的解为；

(2)、解含绝对值的不等式|x+5|＜3得x的取值范围是；

(3)、求含绝对值的方程 $| x - \frac{1}{6} | + | x + \frac{11}{6} | = 2$ 的整数解；

(4)、解含绝对值的不等式|x﹣1|+|x﹣2|＞4．

查看试题解析
20. 阅读理解：我们知道，比较两数（式）大小有很多方法，“作差法”是常用的方法之一，其原理是不等式（或等式）的性质：若 $a - b > 0$ ，则 $a > b$ ；若 $a - b = 0$ ，则 $a = b$ ；若 $a - b < 0$ ，则 $a < b$ .
例：已知 $A = x^{2} + 2 x y$ ， $B = 4 x y - y^{2}$ ，其中 $x \neq y$ ，求证： $A > B$ .

证明： $A - B = (x^{2} + 2 x y) - (4 x y - y^{2}) = x^{2} + 2 x y - 4 x y + y^{2}$ $= x^{2} - 2 x y + y^{2} = {(x - y)}^{2}$ .

∵ $x \neq y$ ，∴ ${(x - y)}^{2} > 0$ ，∴ $A > B$ .

(1)、操作感知：比较大小：
①若 $a < b < 0$ ，则 $a^{3}$ $a b^{2}$ ；

② $m^{2} + 16$ $8 m$ .

(2)、类比探究：已知 $M = 2016 \times 2019$ ， $N = 2017 \times 2018$ ，试运用上述方法比较 $M$ 、 $N$ 的大小，并说明理由.

(3)、应用拓展：已知 $P (m, m - 4)$ ， $Q (m, m^{2} + 3 m)$ 为平面直角坐标系中的两点，小明认为，无论 $m$ 取何值，点 $Q$ 始终在点 $P$ 的上方，小明的猜想对吗？为什么？

查看试题解析
21. 定义：给定两个不等式组 $P$ 和 $Q$ ，若不等式组 $P$ 的任意一个解，都是不等式组 $Q$ 的一个解，则称不等式组 $P$ 为不等式组 $Q$ 的“子集”．
例如：不等式组 $M$ ： ${\begin{array}{l} x > 2 \\ x > 1 \end{array}$ 是 $N$ ： ${\begin{array}{l} x > - 2 \\ x > - 1 \end{array}$ 的“子集”．

(1)、若不等式组： $A$ ： ${\begin{array}{l} x + 1 > 4 \\ x - 1 < 5 \end{array}$ ， $B$ ： ${\begin{array}{l} 2 x - 1 > 1 \\ x > - 3 \end{array}$ ，则其中不等式组是不等式组 $M$ ： ${\begin{array}{l} x > 2 \\ x > 1 \end{array}$ 的“子集” $($ 填A或B）；

(2)、若关于 $x$ 的不等式组 ${\begin{array}{l} x > a \\ x > - 1 \end{array}$ 是不等式组 ${\begin{array}{l} x > 2 \\ x > 1 \end{array}$ 的“子集”，则 $a$ 的取值范围是；

(3)、已知 $a$ ， $b$ ， $c$ ， $d$ 为不互相等的整数，其中 $a < b$ ， $c < d$ ，下列三个不等式组： $A$ ： $a \leq x \leq b$ ， $B$ ： $c \leq x \leq d$ ， $C$ ： $1 < x < 6$ 满足： $A$ 是 $B$ 的“子集”且 $B$ 是 $C$ 的“子集”，求 $a - b + c - d$ 的值．

查看试题解析
22. 定义：对任意一个两位数a，如果a满足个位数字与十位数字互不相同，且都不为零，那么称这个两位数为“湘一数”.将一个“湘一数”的个位数字与十位数字对调后得到一个新的两位数，把这个两位数与原两位数的和与11的商记为 $f (a)$ .例如：a=23，对调个位数字与十位数字得到新两位数32，新两位数与原两位数的和为23+32=55，和与11的商为55÷11=5，所以 $f (23) = 5$ .
根据以上定义，回答下列问题：

(1)、填空：①下列两位数：50、42，33中，“湘一数”为；②计算： $f (45) =$ .

(2)、如果一个“湘一数”b的十位数字是k，个位数字是 $2 (k + 1)$ ，且 $f (b) = 8$ ，请求出“湘一数”b；

(3)、如果一个“湘一数”c，满足 $c - 5 f (c) > 30$ ，求满足条件的c的值.

查看试题解析
23. 某超市销售甲、乙两种型号的电器，其进价分别为180元/台和160元/台，下表是近两周的销售情况（进价、售价均保持不变，利润=售价-进价）：
销售时段
销售数量（台）
销售收入
甲种型号
乙种型号
第一周
3
2
1120
第二周
4
3
1560

(1)、求甲乙两种型号电器的销售单价；

(2)、若超市准备用不多于6000元的金额再采购这两种型号的电器共35台，求甲种型号的电器最多能采购多少台？

(3)、在（2）的条件下，超市销售完这35台电器能否实现利润超过1750元的目标？如果能，请给出相应的采购方案，并说明在这些采购方案中，哪种采购方案利润最大？若不能，请说明理由．

查看试题解析
24. 某商店决定购进A、B两种纪念品．若购进A种纪念品8件，B种纪念品3件，需要95元；若购进A种纪念品5件，B种纪念品6件，需要80元．

(1)、求购进A、B两种纪念品每件各需多少元？

(2)、若该商店决定购进这两种纪念品共100件，考虑市场需求和资金周转，用于购买这100件纪念品的资金不少于750元，但不超过764元，那么该商店共有几种进货方案？

(3)、已知商家出售一件A种纪念品可获利a元，出售一件B种纪念品可获利（5﹣a）元，试问在（2）的条件下，商家采用哪种方案可获利最多？（商家出售的纪念品均不低于成本价）

查看试题解析
25. 材料1：我们把形如 $a x + b y = c$ （ $a$ 、 $b$ 、 $c$ 为常数）的方程叫二元一次方程.若 $a$ 、 $b$ 、 $c$ 为整数，则称二元一次方程 $a x + b y = c$ 为整系数方程.若 $| c |$ 是 $| a |$ ， $| b |$ 的最大公约数的整倍数，则方程有整数解.例如方程 $3 x + 4 y = 2 ， 7 x - 3 y = 5 ， 4 x + 2 y = 6$ 都有整数解；反过来也成立.方程 $6 x + 3 y = 10 和 4 x - 2 y = 1$ 都没有整数解，因为6，3的最大公约数是3，而10不是3的整倍数；4，2的最大公约数是2，而1不是2的整倍数.
材料2：求方程 $5 x + 6 y = 100$ 的正整数解.

解：由已知得： $x = \frac{100 - 6 y}{5} = \frac{100 - 5 y - y}{5} = 20 - y - \frac{y}{5}$ ……①

设 $\frac{y}{5} = k$ （ $k$ 为整数），则 $y = 5 k$ ……②

把②代入①得： $x = 20 - 6 k$ .

所以方程组的解为 ${\begin{array}{l} x = 20 - 6 k \\ y = 5 k \end{array}$ ，

根据题意得： ${\begin{array}{l} 20 - 6 k > 0 \\ 5 k > 0 \end{array}$ .

解不等式组得0＜ $k$ ＜ $\frac{10}{3}$ .所以 $k$ 的整数解是1，2，3.

所以方程 $5 x + 6 y = 100$ 的正整数解是： ${\begin{array}{l} x = 14 \\ y = 5 \end{array}$ ， ${\begin{array}{l} x = 8 \\ y = 10 \end{array}$ ， ${\begin{array}{l} x = 2 \\ y = 15 \end{array}$ .

根据以上材料回答下列问题：

(1)、下列方程中：① $3 x + 9 y = 11$ ，② $15 x - 5 y = 70$ ，③ $6 x + 3 y = 111$ ，④ $27 x - 9 y = 99$ ，⑤ $91 x - 26 = 169$ ，⑥ $22 x + 121 y = 324$ .没有整数解的方程是（填方程前面的编号）；

(2)、仿照上面的方法，求方程 $3 x + 4 y = 38$ 的正整数解；

(3)、若要把一根长30 $m$ 的钢丝截成2 $m$ 长和3 $m$ 长两种规格的钢丝（两种规格都要有），问怎样截才不浪费材料？你有几种不同的截法？（直接写出截法，不要求解题过程）

查看试题解析

销售时段	销售数量（台）		销售收入
销售时段	甲种型号	乙种型号	销售收入
第一周	3	2	1120
第二周	4	3	1560

2023年苏科版数学七年级下册全方位训练卷第十一章 一元一次不等式（进阶版）

一、单选题（每题2分，共16分）

二、填空题（每空3分，共18分）

三、解答题（共9题，共86分）

2023年苏科版数学七年级下册全方位训练卷第十一章一元一次不等式（进阶版）