2023年苏科版数学八年级下册全方位训练卷第十一章 反比例函数(进阶版)
试卷更新日期:2023-04-05 类型:单元试卷
一、单选题(每题3分,共24分)
-
1. 已知函数y=(m-2)是反比例函数,则m的值为( )A、2 B、-2 C、2或-2 D、任意实数2. 已知、、为双曲线上的三个点,且 , 则以下判断正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则3. 将反比例函数y=的图象绕坐标原点O逆时针旋转30°,得到如图的新曲线A(-3,3),B( , )的直线相交于点C、D,则△OCD的面积为( )
 A、3 B、8 C、2 D、4. 如图,一次函数与反比例函数的图象相交于、两点,与轴,轴分别相交于、两点,连接、 . 过点作轴于点 , 交于点 . 设点的横坐标为 . 若 , 则的值为( )
A、3 B、8 C、2 D、4. 如图,一次函数与反比例函数的图象相交于、两点,与轴,轴分别相交于、两点,连接、 . 过点作轴于点 , 交于点 . 设点的横坐标为 . 若 , 则的值为( ) A、1 B、 C、2 D、45. 设双曲线 (k > 0)与直线y=x交于A,B两点(点A在第三象限),将双曲线在第一象限的一支沿射线BA的方向平移,使其经过点A,将双曲线在第三象限的一支沿射线AB的方向平移,使其经过点B,平移后的两条曲线相交于点P,Q两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,PQ为双曲线的“眸径”.当双曲线 (k > 0)的眸径为4时,k的值为( )
A、1 B、 C、2 D、45. 设双曲线 (k > 0)与直线y=x交于A,B两点(点A在第三象限),将双曲线在第一象限的一支沿射线BA的方向平移,使其经过点A,将双曲线在第三象限的一支沿射线AB的方向平移,使其经过点B,平移后的两条曲线相交于点P,Q两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,PQ为双曲线的“眸径”.当双曲线 (k > 0)的眸径为4时,k的值为( )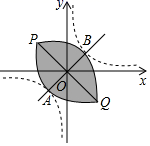 A、 B、 C、2 D、46. 公元前3世纪,古希腊科学家阿基米德发现了“杠杆原理”:杠杆平衡时,阻力×阻力臂=动力×动力臂,当用撬棍撬动一块石头时,发现阻力和阻力臂分别为和 , 关于动力F和动力臂l,下列说法错误的是( )A、F与l的积为定值 B、F随l的增大而减小 C、当l为时,撬动石头至少需要的力 D、F关于l的函数图象位于第一、第三象限7. 如图是4个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作Tm(m为1~4的整数),函数y=(x>0)的图象为曲线L.若曲线L使得T1~T4 , 这些点分布在它的两侧,每侧各2个点,则k的取值范围是( )
A、 B、 C、2 D、46. 公元前3世纪,古希腊科学家阿基米德发现了“杠杆原理”:杠杆平衡时,阻力×阻力臂=动力×动力臂,当用撬棍撬动一块石头时,发现阻力和阻力臂分别为和 , 关于动力F和动力臂l,下列说法错误的是( )A、F与l的积为定值 B、F随l的增大而减小 C、当l为时,撬动石头至少需要的力 D、F关于l的函数图象位于第一、第三象限7. 如图是4个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作Tm(m为1~4的整数),函数y=(x>0)的图象为曲线L.若曲线L使得T1~T4 , 这些点分布在它的两侧,每侧各2个点,则k的取值范围是( ) A、8≤k≤12 B、8≤k<12 C、8<k≤12 D、8<k<128. 呼气式酒精测试仪中装有酒精气体传感器,可用于检测驾驶员是否酒后驾车.酒精气体传感器是一种气敏电阻(图1中的 ), 的阻值随呼气酒精浓度K的变化而变化(如图2),血液酒精浓度M与呼气酒精浓度K的关系见图3.下列说法不正确的是( )
A、8≤k≤12 B、8≤k<12 C、8<k≤12 D、8<k<128. 呼气式酒精测试仪中装有酒精气体传感器,可用于检测驾驶员是否酒后驾车.酒精气体传感器是一种气敏电阻(图1中的 ), 的阻值随呼气酒精浓度K的变化而变化(如图2),血液酒精浓度M与呼气酒精浓度K的关系见图3.下列说法不正确的是( ) A、呼气酒精浓度K越大, 的阻值越小 B、当K=0时, 的阻值为100 C、当K=10时,该驾驶员为非酒驾状态 D、当 时,该驾驶员为醉驾状态
A、呼气酒精浓度K越大, 的阻值越小 B、当K=0时, 的阻值为100 C、当K=10时,该驾驶员为非酒驾状态 D、当 时,该驾驶员为醉驾状态二、填空题(每空3分,共27分)
-
9. 设矩形的一组邻边长分别为x,y,面积是 (S为定值),当 时,矩形的周长为6,则 关于 的函数表达式是 , 自变量 的取值范围是.10. 如图,四边形为矩形,点在第三象限,点关于的对称点为点 , 点 , 都在函数的图象上,轴于点.若的延长线交轴于点 , 当矩形的面积为6时,的值为.
 11. 如图,在平面直角坐标系中,矩形ABCD的对角线AC的中点与坐标原点重合,点E是x轴上一点,连接AE.若AD平分∠OAE,反比例函数y= (k>0,x>0)的图象经过AE上的两点A,F,且AF=EF,△ABE的面积为18,则k的值为 .
11. 如图,在平面直角坐标系中,矩形ABCD的对角线AC的中点与坐标原点重合,点E是x轴上一点,连接AE.若AD平分∠OAE,反比例函数y= (k>0,x>0)的图象经过AE上的两点A,F,且AF=EF,△ABE的面积为18,则k的值为 .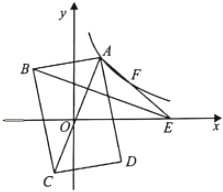 12. 如图,点 均在双曲线 上运动, 轴, ,则 的面积是.
12. 如图,点 均在双曲线 上运动, 轴, ,则 的面积是. 13. 小明要把一篇文章录入电脑,所需时间 与录入文字的速度 (字 )之间的反比例函数关系如图所示,如果小明要在 内完成录入任务,则小明录入文字的速度至少为字 .
13. 小明要把一篇文章录入电脑,所需时间 与录入文字的速度 (字 )之间的反比例函数关系如图所示,如果小明要在 内完成录入任务,则小明录入文字的速度至少为字 .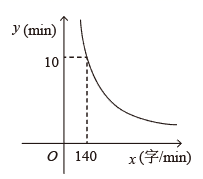 14. 如图,反比例函数 的图象与直线 交于 , 两点(点 在点 右侧),过点 作 轴的垂线,垂足为点 ,连接 , ,图中阴影部分的面积为12,则 的值为.
14. 如图,反比例函数 的图象与直线 交于 , 两点(点 在点 右侧),过点 作 轴的垂线,垂足为点 ,连接 , ,图中阴影部分的面积为12,则 的值为. 15. 在平面直角坐标系xOy中,双曲线y1= (x>0)经过平行四边形ABCD的对称中心Q,双曲线y2= (x>0,0<k<4)经过平行四边形ABCD的顶点B,C,且A(3,0),D(0,4),则k=.
15. 在平面直角坐标系xOy中,双曲线y1= (x>0)经过平行四边形ABCD的对称中心Q,双曲线y2= (x>0,0<k<4)经过平行四边形ABCD的顶点B,C,且A(3,0),D(0,4),则k=. 16. 如图,点为直线上的两点,过两点分别作轴的平行线交双曲线于点 , 若 , 则的值为.
16. 如图,点为直线上的两点,过两点分别作轴的平行线交双曲线于点 , 若 , 则的值为.
三、解答题(共9题,共99分)
-
17. 规定:在平面直角坐标系中,横坐标与纵坐标均为整数的点,叫做整点,点 , 在反比例函数的图象上;
 (1)、m=;(2)、已知 , 过点、D点作直线交双曲线于E点,连接OB,若阴影区域(不包括边界)内有4个整点,求b的取值范围.18. 如图1,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点B在反比例函数y=(k>0)的第一象限内的图象上,OA=4,OC=3,动点P在y轴的右侧,且满足S△PCO=S矩形OABC.
(1)、m=;(2)、已知 , 过点、D点作直线交双曲线于E点,连接OB,若阴影区域(不包括边界)内有4个整点,求b的取值范围.18. 如图1,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点B在反比例函数y=(k>0)的第一象限内的图象上,OA=4,OC=3,动点P在y轴的右侧,且满足S△PCO=S矩形OABC.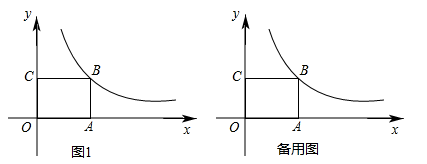 (1)、若点P在这个反比例函数的图象上,求点P的坐标;(2)、连接PO、PC,求PO+PC的最小值;(3)、若点Q是平面内一点,使得以B、C、P、Q为顶点的四边形是菱形,请你直接写出满足条件的所有点Q的坐标.19. 如图,一次函数()的图像与轴交于点 , 与反比例函数()的图像交于点 .
(1)、若点P在这个反比例函数的图象上,求点P的坐标;(2)、连接PO、PC,求PO+PC的最小值;(3)、若点Q是平面内一点,使得以B、C、P、Q为顶点的四边形是菱形,请你直接写出满足条件的所有点Q的坐标.19. 如图,一次函数()的图像与轴交于点 , 与反比例函数()的图像交于点 .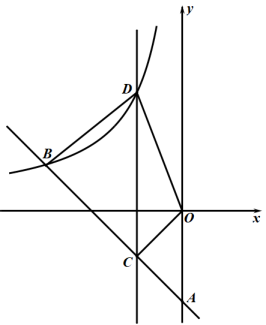
 (1)、b=;k=;(2)、点是线段上一点(不与重合),过点且平行于轴的直线交该反比例函数的图象于点 , 连接 , 若四边形的面积 , 求点的坐标;(3)、将第(2)小题中的沿射线方向平移一定的距离后,得到 , 若点 的对应点恰好落在该反比例函数图象上(如图),求此时点的对应点的坐标.20. 综合与探究
(1)、b=;k=;(2)、点是线段上一点(不与重合),过点且平行于轴的直线交该反比例函数的图象于点 , 连接 , 若四边形的面积 , 求点的坐标;(3)、将第(2)小题中的沿射线方向平移一定的距离后,得到 , 若点 的对应点恰好落在该反比例函数图象上(如图),求此时点的对应点的坐标.20. 综合与探究如图1,反比例函数的图象经过点A,点A的横坐标是-2,点A关于坐标原点O的对称点为点B,作直线 .
 (1)、判断点B是否在反比例函数的图象上,并说明理由;(2)、如图1,过坐标原点O作直线交反比例函数的图象于点C和点D,点C的横坐标是4,顺次连接 , , 和 . 求证:四边形是矩形;(3)、已知点P在x轴的正半轴上运动,点Q在平面内运动,当以点O,B,P和Q为顶点的四边形为菱形时,请直接写出此时点P的坐标.21. 已知一块矩形草坪的两边长分别是2米与3米,现在要把这个矩形按照如图1的方式扩大到面积为原来的2倍,设原矩形的一边加长a米,另一边长加长b米,可得a与b之间的函数关系式b=﹣2.某班“数学兴趣小组”对此函数进一步推广,得到更一般的函数y=﹣2,现对这个函数的图象和性质进行了探究,研究过程如下,请补充完整:
(1)、判断点B是否在反比例函数的图象上,并说明理由;(2)、如图1,过坐标原点O作直线交反比例函数的图象于点C和点D,点C的横坐标是4,顺次连接 , , 和 . 求证:四边形是矩形;(3)、已知点P在x轴的正半轴上运动,点Q在平面内运动,当以点O,B,P和Q为顶点的四边形为菱形时,请直接写出此时点P的坐标.21. 已知一块矩形草坪的两边长分别是2米与3米,现在要把这个矩形按照如图1的方式扩大到面积为原来的2倍,设原矩形的一边加长a米,另一边长加长b米,可得a与b之间的函数关系式b=﹣2.某班“数学兴趣小组”对此函数进一步推广,得到更一般的函数y=﹣2,现对这个函数的图象和性质进行了探究,研究过程如下,请补充完整: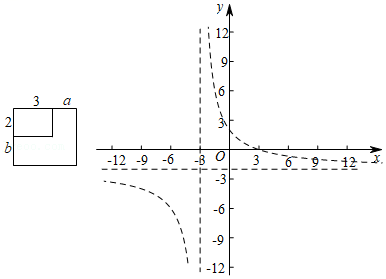 (1)、类比反比例函数可知,函数y=﹣2的自变量x的取值范围是 , 这个函数值y的取值范围是 .(2)、“数学兴趣小组”进一步思考函数y=|﹣2|的图象和性质,请根据函数y=﹣2的图象,画出函数y=|﹣2|的图象;(3)、结合函数y=|﹣2|的图象解答下列问题:
(1)、类比反比例函数可知,函数y=﹣2的自变量x的取值范围是 , 这个函数值y的取值范围是 .(2)、“数学兴趣小组”进一步思考函数y=|﹣2|的图象和性质,请根据函数y=﹣2的图象,画出函数y=|﹣2|的图象;(3)、结合函数y=|﹣2|的图象解答下列问题:①求出方程|﹣2|=0的根;
②如果方程|﹣2|=a有2个实数根,请直接写出a的取值范围.
22. 如图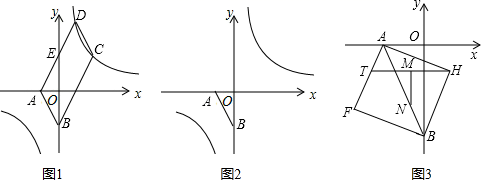
如图1,已知点 , ,且 、 满足 处于平行四边形 的边 与 轴交于点 ,且 为 中点,双曲线 经过 、 两点.
(1)、 , ;(2)、求 点的坐标;(3)、点 在双曲线 上,点 在 轴上(如图2),若以点 、 、 、 为顶点的四边形是平行四边形,请直接写出点 的坐标;(4)、以线段 为对角线作正方形 (如图3),点 是边 上一动点, 是 的中点, ,交 于 ,当 在 上运动时, 的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.23. 在平面直角坐标系内,已知任意两点的坐标 , 我们把称为A、B两点的“横向距离”,记作=.例如: , 则=. (1)、①若点 , 当A、B都在函数的函数图象上时,=.
(1)、①若点 , 当A、B都在函数的函数图象上时,=.②若点 , 当A、B都在函数的函数图象上时,=.
(2)、已知直线交x轴于B点,交y轴于A点,在第一象限内交双曲线于C,D两点,且满足.若恒成立,求m的最大值.(3)、若抛物线与直线在同一坐标平面内交于 , , 且满足下列两个条件:① , ②抛物线过 , 试求的取值范围.24. 图,在平面直角坐标系中,矩形的顶点B的坐标为 , , 分别落在x轴和y轴上,是矩形的对角线,将绕点O逆时针旋转,使点B落在y轴上,得到 , 与相交于点F,反比例函数的图象经过点F,交于点G. (1)、求的值及反比例函数表达式.(2)、在x轴上是否存在一点M,使的值最大?若存在,求出点M;若不存在,说明理由.(3)、在线段上存在这样的点P,使得是等腰三角形,请直接写出的长.25. 某一农家计划利用已有的一堵长为8m的墙,用篱笆圈成一个面积为12m2的矩形ABCD花园,现在可用的篱笆总长为11m.
(1)、求的值及反比例函数表达式.(2)、在x轴上是否存在一点M,使的值最大?若存在,求出点M;若不存在,说明理由.(3)、在线段上存在这样的点P,使得是等腰三角形,请直接写出的长.25. 某一农家计划利用已有的一堵长为8m的墙,用篱笆圈成一个面积为12m2的矩形ABCD花园,现在可用的篱笆总长为11m.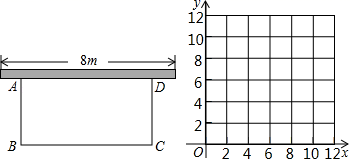 (1)、若设 , .请写出y关于x的函数表达式;(2)、若要使11m的篱笆全部用完,能否围成面积为15m2的花园?若能,请求出长和宽;若不能,请说明理由;(3)、若要使11m的篱笆全部用完,请写出y关于x的第二种函数解析式.请在坐标系中画出两个函数的图象,观察图象,满足条件的围法有几种?请说明理由.
(1)、若设 , .请写出y关于x的函数表达式;(2)、若要使11m的篱笆全部用完,能否围成面积为15m2的花园?若能,请求出长和宽;若不能,请说明理由;(3)、若要使11m的篱笆全部用完,请写出y关于x的第二种函数解析式.请在坐标系中画出两个函数的图象,观察图象,满足条件的围法有几种?请说明理由.