2023年苏科版数学八年级下册全方位训练卷11.3 用反比例函数解决问题

试卷更新日期：2023-04-05 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共24分）

1. 如图，直线 $y = a x + b$ 与x轴相交于点A $(2 ， 0)$ ，与函数 $y = \frac{k}{x}$ 的图象交于点B，C，点B的横坐标是8，点C的横坐标是 $- 6$ ，则不等式组 $0 < a x + b < \frac{k}{x}$ 的解集是（）

A、 $- 6 < x < 2$ B、 $- 6 < x < 0$ C、 $- 6 < x < 8$ D、 $0 < x < 2$

查看试题解析
2. 小明乘车从县城到怀化，行车的速度 $v (k m / h)$ 和行车时间 $t (h)$ 之间函数图是（）

A、 B、 C、 D、

查看试题解析
3. 如图，某加油站计划在地下修建一个容积为 $2 \times 1 0^{4} m^{3}$ 的圆柱形石油储存室，则储存室的底面积S（单位： $m^{2}$ ）与其深度h（单位：m）的函数图象大致是（）

A、 B、 C、 D、

查看试题解析
4. 如图，在平面直角坐标系中，直线 $y = - \frac{2}{3} x$ 与直线 $y = - \frac{2}{3} x + 2$ 分别与函数 $y = \frac{k}{x}$ $(x < 0)$ 的图象交点 $A$ 、 $B$ 两点，连结 $A B$ 、 $O B$ ，若 $△ O A B$ 的面积为 $3$ ，则 $k$ 的值为（）．

A、-2 B、-3 C、-4 D、-6

查看试题解析
5. 如图是4个台阶的示意图，每个台阶的高和宽分别是1和2，每个台阶凸出的角的顶点记作T_m（m为1～4的整数），函数y＝ $\frac{k}{x}$ （x＞0）的图象为曲线L．若曲线L使得T₁～T₄ ，这些点分布在它的两侧，每侧各2个点，则k的取值范围是（）

A、8≤k≤12 B、8≤k＜12 C、8＜k≤12 D、8＜k＜12

查看试题解析
6. 木板对地面的压强p（Pa）是木板面积S（m²）的反比例函数，其图象如图所示，当压强不超过400 Pa时，木板的面积应（）

A、不大于1.5 m² B、不小于1.5 m² C、不大于 $\frac{8}{3}$ m² D、不小于 $\frac{8}{3}$ m²

查看试题解析
7. 已知蓄电池的电压为定值，使用蓄电池时，电流I（单位：A）与电阻R（单位： $Ω$ ）是反比例函数关系，它的图象如图所示．下列说法正确的是（）

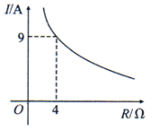A、函数解析式为 $I = \frac{13}{R}$ B、蓄电池的电压是18V C、当 $I \leq 10 A$ 时， $R \geq 3.6 Ω$ D、当 $R = 6 Ω$ 时， $I = 4 A$

查看试题解析
8. 某校科技小组进行野外考察，利用铺垫木板的方式通过了一片烂泥湿地．当人和木板对湿地的压力一定时，人和木板对地面的压强p（Pa）是木板面积S（m²）的反比例函数，其图象如图，点A在反比例函数图象上，坐标是（8，30），当压强p（Pa）是4800Pa时，木板面积为（）m²

A、0.5 B、2 C、0.05 D、20

查看试题解析

二、填空题（每题3分，共24分）

9. 已知一次函数y＝ $\frac{1}{2}$ x-2的图象与反比例函数y＝ $\frac{3}{x}$ 的图象相交于点P（a，b），则 $\frac{2}{a} - \frac{1}{b}$ 的值是．

查看试题解析
10. 若一次函数 $y = k x + 1$ 的图象与反比例函数 $y = \frac{1}{x}$ 的图象没有公共点，则实数k的取值范围是

查看试题解析
11. 一辆汽车前灯电路上的电压U（V）保持不变，通过灯泡的电流强度I（A）是电阻R（Ω）的反比例函数.若当电阻为30Ω时，通过灯泡的电流强度为0.40A，则当电阻为50Ω时，通过灯泡的电流强度为 A.

查看试题解析
12. 小刚欲用撬棍撬动一块大石头,已知阻力和阻力臂不变,分别为900牛顿和0.5米,则当动力臂为1.5米时,撬动石头需要的力大于牛顿.(提示根据杠杆原理:阻力x阻力臂=动力x动力臂)

查看试题解析
13. 某产品的进价为50元，该产品的日销量 $y$ （件）是日销价 $x$ （元）的反比例函数，且当售价为每件100元时，每日可售出40件，为获得日利润为1500元，售价应定为.

查看试题解析
14. 如图，一块砖的A，B，C三个面的面积之比是 $1 ： 5 ： 3$ ．如果A，B，C三个面分别向下放在地上，地面所受压强分别为 $P_{1}$ ， $P_{2}$ ， $P_{3}$ ，压强的计算公式为 $P = \frac{F}{S}$ ，其中P是压强，F是压力，S是受力面积，则 $P_{1}$ ， $P_{2}$ ， $P_{3}$ 的大小关系为（用小于号连接）．

查看试题解析
15. 青藏铁路是当今世界上海拔最高、线路最长的高原铁路，因路况、季节、天气等原因行车的平均速度在 $250 ~ 360$ （千米/小时）之间变化，铁路运行全程所需要的时间（小时）与运行的平均速度（千米/小时）满足如图所示的函数关系，列车运行的平均速度最大和列车运行的平均速度最小时全程所用时间相差小时．

查看试题解析
16. 如图，点A、B分别在x轴的正半轴和负半轴上，以AB为边在x轴的上方作正方形ABCD，正方形ABCD对角线的交点坐标为I（a，b），在正方形ABCD的内部作正方形OPMN，使得O、P、M、N分别落在AB、BC、CD、DA上，若双曲线 $y = \frac{k}{x}$ 经过点N和点I，则 $\frac{a}{b}$ 的值是．

查看试题解析

三、解答题（共10题，共72分）

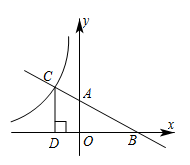
17. 直线 $y = x + 1$ 与反比例函数 $y = \frac{k}{x}$ （其中 $k \neq 0$ ）的图象交于 $A (- 2, - 1)$ 、 $B (m, n)$ ，求点 $B$ 的坐标.

查看试题解析
18. 已知近视眼镜的度数y（度）与镜片焦距x（米）成反比例关系，且400度近视眼镜镜片的焦距为0.25米．小慧原来戴400度的近视眼镜，经过一段时间的矫正治疗后，现在只需戴镜片焦距为0.4米的眼镜了，求小慧所戴眼镜的度数降低了多少度．

查看试题解析
19. 如图所示，直线 $y = - \frac{1}{2} x + 2$ 交坐标轴于A ， B两点，与反比例函数 $y = \frac{k}{x} (x < 0)$ 交于点C ，过点C作x轴的垂线，垂足为D ．若 $A O ： C D = 2 ： 3$ ，求k的值．

查看试题解析
20. 如图，已知反比例函数 $y = - \frac{4}{x} (k \neq 0)$ 与直线 $y = - 2 x + 2$ 交于 $A (- 1 ， 4)$ ， B两点.

(1)、求点B的坐标；

(2)、根据函数图象，直接写出关于x的不等式 $- 2 x + 2 < - \frac{4}{x}$ 的解集.

查看试题解析
21. 如图，点 $A (1 ， 6)$ 和 $B (n ， 2)$ 是一次函数 $y_{1} = k x + b$ 的图像与反比例函数 $y_{2} = \frac{m}{x} (x > 0)$ 的图像的两个交点.

(1)、求m、n的值；

(2)、求一次函数的表达式；

(3)、设点P是y轴上的一个动点，当 $△ P A B$ 的周长最小时，求点P的坐标；

(4)、在（3）的条件下，设点D是坐标平面内一个动点，当以点A、B、C、D为顶点的四边形是平行四边形时，请直接写出符合条件的所有点D的坐标.

查看试题解析
22. 如图是某游乐园“水上滑梯”的侧面示意图，其中BD段可看成双曲线 $y = \frac{k}{x} (x > 0)$ 的一部分，矩形OABC是向上攀爬的阶梯部分．以O为中心建立平面直角坐标系，使点A和点C分别落在x轴和y轴的正半轴上．已知OC=5米，入口平台BC=1.8米，滑梯的出口D点到水面的距离DE为0.75米（O、A、E在一条直线上）．求B、D之间的水平距离AE的长．

查看试题解析
23. 规定：在平面直角坐标系中，横坐标与纵坐标均为整数的点，叫做整点，点 $A (2 ， 2)$ ， $B (m ， 1)$ 在反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象上；

(1)、m=；

(2)、已知 $b > 0$ ，过点 $C (- 4 b ， 0)$ 、D点 $(0 ， b)$ 作直线交双曲线 $y = \frac{k}{x} (x > 0)$ 于E点，连接OB，若阴影区域（不包括边界）内有4个整点，求b的取值范围．

查看试题解析
24. 1896年，挪威生理学家古德贝发现，每个人有一条腿迈出的步子比另一条腿迈出的步子长的特点，这就导致每个人在蒙上眼睛行走时，虽然主观上沿某一方向直线前进，但实际上走出的是一个大圆圈!这就是有趣的“嗐转圈”现象.经研究，某人蒙上眼睛走出的大圆圈的半径y/米是其两腿迈出的步长之差x/厘米（ $x > 0$ ）的反比例函数，y与x之间有如表关系：
$x /$ 厘米
1
2
3
5
$y /$ 米
14
7
$\frac{14}{3}$
2.8
请根据表中的信息解决下列问题：

(1)、求出y与x之间的函数解析式；

(2)、若某人蒙上眼睛走出的大圆圈的半径为35米，则其两腿迈出的步长之差是多少厘米？

查看试题解析
25. 《城镇污水处理厂污染物排放标准》中硫化物的排放标准为 $1.0 m g / L$ .某污水处理厂在自查中发现，所排污水中硫化物浓度超标，因此立即整改，并开始实时监测.据监测，整改开始第60小时时，所排污水中硫化物的浓度为 $5 m g / L$ ；从第60小时开始，所排污水中硫化物的浓度 $y (m g / L)$ 是监测时间x（小时）的反比例函数，其图象如图所示.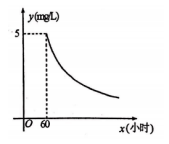

(1)、求y与x的函数关系式；

(2)、整改开始第100小时时，所排污水中硫化物浓度为 $m g / L$ ；

(3)、按规定所排污水中硫化物的浓度不超过 $0.8 m g / L$ 时，才能解除实时监测，此次整改实时监测的时间至少为多少小时？

查看试题解析
26. 1896年，挪威生理学家古德贝发现，每个人有一条腿迈出的步子比另一条腿迈出的步子长的特点，这就导致每个人在蒙上眼睛行走时，虽然主观上沿某一方向直线前进，但实际上走出的是一个大圆圈！这就是有趣的“瞎转圈”现象.经研究，某人蒙上眼睛走出的大圆圈的半径y/米是其两腿迈出的步长之差x/厘米( $x > 0$ )的反比例函数，其图象如下图所示所示.请根据图象中的信息解决下列问题：

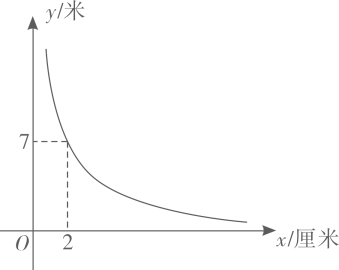(1)、求y与x之间的函数表达式；

(2)、当某人两腿迈出的步长之差为0.5厘米时，他蒙上眼睛走出的大圆圈的半径为多少米？

(3)、若某人蒙上眼睛走出的大圆圈的半径不小于35米，则其两腿迈出的步长之差最多是多少厘米？

查看试题解析

$x /$ 厘米	1	2	3	5
$y /$ 米	14	7	$\frac{14}{3}$	2.8