2023年苏科版数学八年级下册全方位训练卷10.3 分式的加减

试卷更新日期：2023-04-05 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共24分）

1. 计算 $\frac{1}{1 - x} + \frac{x^{2}}{x - 1}$ 时，第一步变形正确的是（）

A、1+x² B、1-x² C、 $\frac{1}{1 - x} + \frac{x^{2}}{1 - x}$ D、 $\frac{1}{1 - x} - \frac{x^{2}}{1 - x}$

查看试题解析
2. 计算 $\frac{18}{x^{2} - 3 x} - \frac{2 x}{x - 3}$ 的结果是（）

A、 $\frac{2 x + 6}{x}$ B、 $- \frac{2 x + 6}{x}$ C、 $\frac{2 x - 6}{x}$ D、 $- \frac{2 x - 6}{x}$

查看试题解析
3. 下列等式成立的是（）

A、 $\frac{1}{a} + \frac{2}{a} = \frac{3}{2 a}$ B、 $\frac{a}{a - 1} + \frac{1}{1 - a} = \frac{a + 1}{a - 1}$ C、 $\frac{x}{x + 1} + \frac{1}{x + 1} = 1$ D、 $\frac{1}{{(m - 2)}^{2}} - \frac{m - 1}{{(m - 2)}^{2}} = \frac{m - 2}{{(m - 2)}^{2}}$

查看试题解析
4. $\frac{x}{x - 1} = () - \frac{2 x - 1}{1 - x}$ ，括号里应填（）

A、-1 B、1 C、-2 D、任意实数

查看试题解析
5. 若 $x y = - 6$ ，其中 $x > y$ ，则下列分式的值一定比 $\frac{y}{x}$ 的值大的是（）

A、 $\frac{3 y}{3 x}$ B、 $\frac{3 y}{x}$ C、 $- \frac{3}{x}$ D、 $\frac{y + 3}{x}$

查看试题解析
6. 如果 $x > y > 1$ ，那么 $\frac{y - 1}{x - 1} - \frac{y}{x}$ 的值是（）

A、正数 B、负数 C、零 D、不确定

查看试题解析
7. 如图，若x为正整数，则表示1- $\frac{1}{x + 1}$ 的值的点落在（）

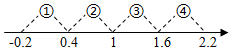A、段① B、段② C、段③ D、段④

查看试题解析
8. 照相机成像应用了一个重要原理，用公式 $\frac{1}{f} = \frac{1}{u} + \frac{1}{v} (v \neq f)$ 表示，其中f表示照相机镜头的焦距，u表示物体到镜头的距离，v表示胶片（像）到镜头的距离．已知f，v，则u＝（）

A、 $\frac{f v}{f - v}$ B、 $\frac{f - v}{f v}$ C、 $\frac{f v}{v - f}$ D、 $\frac{v - f}{f v}$

查看试题解析

二、填空题（每空3分，共27分）

9. 化简 $\frac{x}{x - 3} + \frac{x - 6}{x - 3}$ ，结果等于．

查看试题解析
10. 若 $\frac{2 x - 3}{x + 1} = A - \frac{5}{x + 1}$ ，则 $A$ 是.

查看试题解析
11. 若 $\frac{4 x - 1}{（ x + 2 ）（ x - 1 ）} = \frac{M}{x + 2} + \frac{1}{x - 1}$ ，则整式M= ．

查看试题解析
12. 已知 $x = \sqrt{3} + 2$ ， $y = \sqrt{3} - 2$ ，则代数式 $\frac{y}{x} + 2 + \frac{x}{y}$ 的值是．

查看试题解析
13. 某药品原来每盒p元，现在每盒提高3元，用200元买这种药品现在比原来少买盒．

查看试题解析
14. 设实a，b，c满足： $a + b + c = 3 ， a^{2} + b^{2} + c^{2} = 4$ ，则 $\frac{a^{2} + b^{2}}{2 - c} + \frac{b^{2} + c^{2}}{2 - a} + \frac{c^{2} + a^{2}}{2 - b}$ = ．

查看试题解析
15. 已知 $x$ 为整数，且 $\frac{2}{x + 3} + \frac{2}{3 - x} + \frac{2 x + 18}{x^{2} - 9}$ 为整数，则所有符合条件的 $x$ 值的和为．

查看试题解析
16. 学习了“分式的加减法”的相关知识后，小明同学画出了如图：
请问他画的图中①代表的计算步骤为， ②代表的计算步骤为．

查看试题解析

三、计算题（共3题，共26分）

17. 计算.

(1)、 $\frac{x + 2}{x + 1} - \frac{x - 1}{x + 1}$ ；

(2)、 $\frac{x^{2}}{x - 1} + \frac{x}{1 - x}$ ；

(3)、 $\frac{a + 2}{{(a - 2)}^{2}} - \frac{4}{{(2 - a)}^{2}}$ ；

(4)、 $\frac{2 x^{2} + 1}{x^{2} - 5 x + 6} - \frac{x^{2} - 1}{x^{2} - 5 x + 6} + \frac{4 - 5 x}{x^{2} - 5 x + 6}$ .

查看试题解析
18. 计算： $\frac{1}{x - 4} - \frac{1}{x - 5} - \frac{1}{x - 7} + \frac{1}{x - 8}$ .

查看试题解析
19. 化简： $\frac{1}{(x + 1) (x + 2)} + \frac{1}{(x + 2) (x + 3)} +$ $\frac{1}{(x + 3) (x + 4)}$

查看试题解析

四、综合题（共6题，共43分）

20. 已知x为整数，且 $\frac{2}{x + 3}$ + $\frac{2}{3 - x}$ + $\frac{2 x + 18}{x^{2} - 9}$ 化简结果为整数，求出所有符合条件的x值．

查看试题解析
21. 已知 $a, b$ 实数满足 $a b = 1$ ，若 $M = \frac{1}{1 + a} + \frac{1}{1 + b}$ ， $N = \frac{a}{1 + a} + \frac{b}{1 + b}$ ，请你猜想 $M$ 与 $N$ 的数量关系，并证明．

查看试题解析
22. 学习分式运算过程中，老师布置了这样一个任务：依据下面的流程图，计算 $\frac{a}{a - b} - \frac{2 a b}{a^{2} - b^{2}}$ ．

(1)、依据上面流程图计算 $\frac{a}{a - b} - \frac{2 a b}{a^{2} - b^{2}}$ 时，需要经历的路径是（只填写序号）；

(2)、依据（1）中路径写出正确解答过程．

查看试题解析
23. 化简： $\frac{1}{x - 1} + \frac{2}{x + 2}$ ．小明的解法如下框：

解：原式 $= x + 2 + 2 (x - 1)$

$= x + 2 + 2 x - 2$

$= 3 x$

小明的解答是否正确？若正确，请在框内打“√”；若错误，请写出你的解答过程．

查看试题解析
24. 阅读下列材料：通过小学的学习我们知道，分数可分为“真分数”和“假分数”，而假分数都可化为带分数，如： $\frac{8}{3} = \frac{6 + 2}{3} = 2 + \frac{2}{3} = 2 \frac{2}{3}$ .我们定义：在分式中，对于只含有一个字母的分式，当分子的次数大于或等于分母的次数时，我们称之为“假分式”；当分子的次数小于分母的次数时，我们称之为“真分式”.如 $\frac{x - 1}{x + 1}$ ， $\frac{x^{2}}{x - 1}$ 这样的分式就是假分式；再如： $\frac{3}{x + 1}$ ， $\frac{2 x}{x^{2} + 1}$ 这样的分式就是真分式.类似的，假分式也可以化为带分式（即：整式与真分式的和的形式）.如： $\frac{x - 1}{x + 1} = \frac{(x + 1) - 2}{x + 1} = 1 - \frac{2}{x + 1}$ ；
解决下列问题：

(1)、分式 $\frac{5}{x}$ 是分式（填“真”或“假”）；

(2)、 $\frac{x^{2}}{x - 1}$ 将假分式化为带分式；

(3)、如果 $x$ 为整数，分式 $\frac{3 x - 2}{x + 1}$ 的值为整数，求所有符合条件的 $x$ 的值.

查看试题解析
25. （阅读理解）
我们在分析解决某些数学问题时，经常要比较两个数或代数式的大小，而解决问题的策略一般要进行一定的转化，其中“作差法”就是常用的方法之一，所谓“作差法”：就是通过作差、变形，并利用差的符号确定它们的大小，即要比较代数式 $M$ 、 $N$ 的大小，只要作出它们的差 $M - N$ ，若 $M - N > 0$ ，则 $M > N$ ；若 $M - N = 0$ ，则 $M = N$ ；若 $M - N < 0$ ，则 $M < N$ .

（解决问题）

小丽和小颖分别两次购买同一种商品，小丽两次都买了 $m$ 千克商品，小颖两次购买商品均花费 $n$ 元，已知第一次购买该商品的价格为 $a$ 元 $/$ 千克，第二次购买该商品的价格为 $b$ 元 $/$ 千克（ $a$ ， $b$ 是整数，且 $a \neq b$ ）

(1)、小丽和小颖两次所购买商品的平均价格分别是多少元 $/$ 千克？

(2)、请用作差法比较小丽和小颖两次所购买商品的平均价格的高低.

查看试题解析