2023年浙教版数学七年级下学期高分速效复习5 整式的乘除（基础版）

试卷更新日期：2023-04-05 类型：复习试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列运算正确的是（）

A、 $a^{3} \cdot a^{5} = a^{8}$ B、 $a^{5} + a^{5} = a^{10}$ C、 ${(- a^{3})}^{2} = - a^{5}$ D、 ${(a b)}^{2} = a b^{2}$

查看试题解析
2. 计算 $- 3 x^{2} \cdot (- 3 x^{3})$ 的结果是（）

A、 $- 6 x^{5}$ B、 $9 x^{5}$ C、 $- 2 x^{6}$ D、 $2 x^{6}$

查看试题解析
3. 长方形一边长为 $2 a + b ，$ 另一边比它小 $a - b$ 则长方形面积为（）

A、 $2 a^{2} + a b - b^{2}$ B、 $2 a^{2} + a b$ C、 $4 a^{2} + 4 a b + b^{2}$ D、 $2 a^{2} + 5 a b + 2 b^{2}$

查看试题解析
4. 若 $(x + 3) (x - 5) = x^{2} + m x - 15$ ，则 $m$ 的值为（）

A、2 B、-2 C、5 D、-5

查看试题解析
5. 下列多项式乘法，能用平方差公式计算的是（）

A、 $(- 3 x - 2) (3 x + 2)$ B、 $(- a - b) (- b + a)$ C、 $(- 3 x + 2) (2 - 3 x)$ D、 $(3 x + 2) (2 x - 3)$

查看试题解析
6. 已知：a＋b＝m，ab＝－4，化简（a－2）（b－2）的结果是（）.

A、6 B、2m－8 C、2m D、－2m

查看试题解析
7. 已知空气的单位体积质量是 $0.001239 g / c m^{3}$ ，将数据0.001239用科学记数法表示为（）

A、 $1.239 \times 1 0^{- 3}$ B、 $1.239 \times 1 0^{- 2}$ C、 $0.1239 \times 1 0^{- 2}$ D、 $12.39 \times 1 0^{- 4}$

查看试题解析
8. 计算 ${(\frac{1}{3})}^{0} \times {(\frac{1}{5})}^{- 2}$ 的结果是（）

A、 $\frac{1}{10}$ B、 $- \frac{1}{10}$ C、25 D、 $- \frac{1}{25}$

查看试题解析
9. 墨迹污染了等式32x³4x＝8x²（x≠0）中的运算符号，则污染的是（）

A、+ B、- C、× D、÷

查看试题解析
10. 如图，有甲、乙、丙三种纸片各若干张，其中甲、乙分别是边长为a，b的正方形，丙是长为b，宽为a的长方形．若同时用甲、乙、丙纸片分别为4张、9张、12张拼成正方形，则拼成的正方形的边长为（）

A、a+2b B、a+3b C、2a+3b D、3a+2b

查看试题解析

二、填空题（每题3分，共18分）

11. 若 $3^{m} = 2$ ， $3^{n} = 5$ ，则 $3^{m + 2 n} =$ ．

查看试题解析
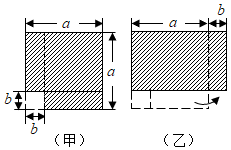
12. 当（a- $\frac{1}{3}$ ）⁰＝1时，a的取值范围是.

查看试题解析
13. 若 $(1 + m) (2 + m) = 3$ ，则 $(1 + m)^{2} + (2 + m)^{2} =$ .

查看试题解析
14. 已知a是－2的相反数，且|b＋1|＝0，则[－3a²(ab²＋2a)＋4a(－ab)²]÷(－4a)的值为．

查看试题解析
15. 某同学计算一个多项式乘 $- 3 x^{2}$ 时，因抄错符号，算成了加上 $- 3 x^{2}$ ，得到的答案是 $x^{2} - \frac{1}{2} x + 1$ ，那么正确的计算结果是．

查看试题解析
16. 将图（甲）中阴影部分的小长方形变换到图（乙）位置，根据两个图形的面积关系得到的恒等式是：.

查看试题解析

三、计算题（共2题，共20分）

17. 计算：

(1)、 $(- 1)^{2022} \times (π - 2)^{0} + | - 5 | + (\frac{1}{2})^{- 2}$ ；

(2)、 $(- \frac{1}{3} a^{2} b)^{2} \cdot 9 a b^{3} \div a^{4} b^{3}$ ；

(3)、 $(\frac{2}{3} m^{2} n - 6 m n) \cdot \frac{3}{2} m n^{2}$ ；

(4)、 $(x + y + 1) (x + y - 1)$ ．

查看试题解析
18. 利用公式（平方差公式或完全平方公式）计算下列各题：

(1)、 $97 \times 103$

(2)、 $99 8^{2}$

查看试题解析

四、解答题（共4题，共26分）

19. 先化简，再求值：

(1)、[(x＋2y²)²－(x＋y²)(x－y²)－5y⁴]÷2y，其中x＝－2，y＝ $\frac{1}{4}$ ；

(2)、(2a＋b)(2a－b)－(a－2b)²＋(6a⁴－4a³)÷(－2a²)，其中a＝ $\frac{1}{2}$ ， b＝1.

查看试题解析
20. 已知：a=2⁵⁵ ， b=3⁴⁴ ， c=5³³比比较abc的大小

查看试题解析
21. 已知多项式（2x+1）（x²+ax+2）的结果中不含有x²项（a是常数），求代数式a²+a+ $\frac{1}{4}$ 的值.

查看试题解析
22. 若 $a^{m} = a^{n} (a > 0$ 且 $a \neq 1$ ， m、n是正整数 $)$ ，则 $m = n$ .利用上面结论解决下面的问题：

(1)、如果 $2 \div 8^{x} \cdot 1 6^{x} = 2^{5}$ ，求x的值；

(2)、如果 $2^{x + 2} + 2^{x + 1} = 24$ ，求x的值；

查看试题解析

五、综合题（共3题，共26分）

23. 某同学在计算一个多项式M乘以-2a时，因抄错运算符号，算成了加上-2a，得到的结果是a+2a-1，

(1)、求这个多项式M；

(2)、求出正确的运算结果．

查看试题解析
24. 阅读下列材料：
我们知道对于二次三项式 $a^{2} + 2 a b + b^{2}$ 可以利用完全平方公式，将它变形为 ${(a + b)}^{2}$ 的形式．但是对于一般的二次三项式 $x^{2} + b x + c$ 就不能直接应用完全平方公式了，我们可以在二次三项式中先加上原式中一次项系数的一半的平方即 $(\frac{b}{2})^{2}$ ，使其凑成完全平方式，再减去 $(\frac{b}{2})^{2}$ ，使整个式子的值不变，这样就有 $x^{2} + b x + c = {(x + \frac{b}{2})}^{2} + m$ ．例如 $x^{2} - 6 x + 1$ ＝ $x^{2} - 6 x + 9 - 9 + 1$ ＝ ${(x - 3)}^{2} - 8$ ．
请根据上述材料解决下列问题：

(1)、将多项式 $x^{2} - 4 x + 3$ 变形为 $(x + m)^{2} + n$ 的形式；

(2)、当x，y分别取何值时 $x^{2} + y^{2} - 4 x + 6 y + 28$ 有最小值？求出这个最小值；

(3)、若 $m = a^{2} + b^{2} - 1$ ， $n = 2 a - 4 b - 7$ ，则m与n的大小关系是．

查看试题解析
25. 某植物园中有如图所示的A、B两个园区，已知A园区为长方形，其长为 $(x + y)$ 米，宽为 $(x - y)$ 米；B园区为正方形，边长为 $(x - y)$ 米．

(1)、请用代数式表示A、B两个园区的面积之和并化简；

(2)、现在根据实际需要对B园区进行改造，将其改造为长方形，宽保持原长度不变，长比原边长增加 $(3 x - 2 y)$ 米，用代数式表示改造后B园区的面积并化简．

查看试题解析