2023学年广西中考数学模拟冲刺卷（百色卷）

试卷更新日期：2023-04-04 类型：中考模拟

进入出卷网下载

一、单选题（每题3分，共36分）

1. $- \frac{1}{2023}$ 的倒数是（）

A、2023 B、 $\frac{1}{2023}$ C、 $- 2023$ D、 $- \frac{1}{2022}$

查看试题解析
2. 如下图，直线AD、BE被直线BF和AC所截，下列说法正确的是（）

A、∠3与∠4是同旁内角 B、∠2与∠5是同位角 C、∠6与∠1是内错角 D、∠2与∠6是同旁内角

查看试题解析
3. 一个布袋里装有5个球，其中3个红球，2个白球，每个球除颜色外其余都相同，则从布袋里任意摸出一个球是红球的概率是（　　）

A、 $\frac{3}{10}$ B、 $\frac{1}{3}$ C、 $\frac{3}{5}$ D、 $\frac{1}{5}$

查看试题解析
4. 已知 $x = 4$ 是关于x的方程 $3 x + 2 a = 0$ 的一个解，则a的值是（）

A、 $- 2$ B、 $- 4$ C、 $- 6$ D、 $- 8$

查看试题解析
5. 一个几何体如图1放置，如图2可能是它的（）

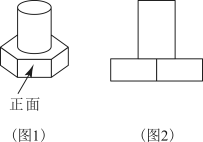A、主视图 B、左视图 C、俯视图 D、不能确定

查看试题解析
6. 如图，在平面直角坐标系中， $△ A B C$ 与 $△ D E F$ 关于原点 $O$ 位似，且 $O B = 2 O E$ ，若 $S_{△ A B C} = 4$ ，则 $S_{△ D E F}$ 为（）

A、 $1$ B、 $2$ C、 $\frac{1}{2}$ D、 $\frac{3}{2}$

查看试题解析
7. 某小组长统计组内5人一天在课堂上的发言次数分别为3，3，0，4，5.关于这组数据，下列说法错误的是（）

A、众数是3 B、中位数是0 C、平均数是3 D、极差是5

查看试题解析
8. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
9. 如图， $△ A B C$ 中， $A B = C B$ ， $∠ A B C < 90 °$ ，尺规作图痕迹如下．
结论Ⅰ：点 $O$ 一定为 $△ A B C$ 的内心；
结论Ⅱ：连接 $O C$ ， $M N$ ，则 $M N < O C$ ．
对于结论Ⅰ和Ⅱ，下列判断正确的是（）

A、Ⅰ和Ⅱ都对 B、Ⅰ和Ⅱ都不对 C、Ⅰ不对，Ⅱ对 D、Ⅰ对，Ⅱ不对

查看试题解析
10. 如图，将 $△ A B C$ 先向上平移1个单位，再绕点P按逆时针方向旋转 $90 °$ ，得到 $△ A^{'} B^{'} C'$ ，则点A的对应点 $A'$ 的坐标是（）

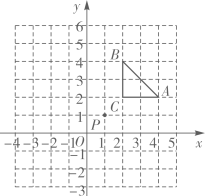A、（0，4） B、（2，-2） C、（3，-2） D、（-1，4）

查看试题解析
11. 如图所示分割正方形，各图形面积之间的关系验证了一个等式，这个等式是（）

A、 ${(y + x)}^{2} = y^{2} + 2 x y + x^{2}$ B、 ${(y - x)}^{2} = y^{2} - 2 x y + x^{2}$ C、 $(y - x) (y + x) = y^{2} - x^{2}$ D、 ${(y + x)}^{2} - {(y - x)}^{2} = 4 x y$

查看试题解析
12. 若点O是等腰△ABC的外心，且∠BOC＝60°，底边BC＝2，则△ABC的面积为（）

A、2＋ $\sqrt{3}$ B、 $\frac{2 \sqrt{3}}{3}$ C、2＋ $\sqrt{3}$ 或2－ $\sqrt{3}$ D、4＋2 $\sqrt{3}$ 或2－ $\sqrt{3}$

查看试题解析

二、填空题（每空3分，共18分）

13. 点A在数轴上距离原点3个单位长度，将A向右移动4个单位长度，再向左移动7个单位长度，此时点A表示的数是。

查看试题解析
14. 因式分解 $y^{2} - 4 x^{2}$ 的结果是．

查看试题解析
15. 如图，若 $△ A B D ≌ △ A C E$ ，且 $∠ 1 = 45 °$ ， $∠ A D B = 95 °$ ，则 $∠ B =$ °.

查看试题解析
16. 《九章算术》卷九勾股第五题原文“今有木长二丈，围之三尺.葛生其下，缠木七周，上与木齐.问葛几何？”题目大意为：现有一棵大树，长为2丈，周长为3尺.葛就生长在树下，缠绕了大树七周，顶端与树一样齐.问葛有多长？葛为尺（1丈 $= 10$ 尺）.

查看试题解析
17. 某人购进一批苹果到集贸市场零售，已知卖出的苹果数量y（千克）与售价x（元/千克）之间的关系如图所示，成本为5元/千克，现以8元/千克的价格卖出，挣得元.（用含k的式子表示）

查看试题解析

18. 某网络公司拟招收职员一名，从学历、经验和工作态度三个方面对甲、乙、丙三名应聘者进行了初步测试，测试成绩如下表：

应聘者项目	甲	乙	丙
学历	7	9	8
经验	8	7	7
工作态度	6	8	5

如果将学历、经验和工作态度三项得分按照 $1 : 2 : 2$ 的比例确定个人的最终得分，并以此为依据确定录用，那么将被录用的是．

查看试题解析

三、解答题（共8题，共66分）

19. 计算： ${(- 1)}^{2} + {(- \frac{1}{3})}^{- 1} - {(3 - π)}^{0}$ ．

查看试题解析
20. 解不等式（组）：

(1)、 $2 (x + 1) - 3 \leq 3 (x - 1)$ ；

(2)、 ${\begin{array}{l} 2 x + 1 \geq 1 \\ \frac{1 + 2 x}{3} > x - 1 \end{array}$ 并把不等式组的解集在数轴上表示出来．

查看试题解析
21. 如图，一次函数 $y_{1} = k_{1} x + b$ （k₁、b为常数，k₁≠0）的图象与反比例函数 $y_{2} = \frac{k_{2}}{x}$ $(k_{2} \neq 0 ， x > 0)$ 的图象交于点A（m，8）与点B（4，2）．

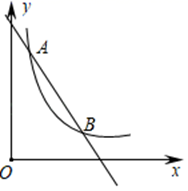
①

(1)、求一次函数与反比例函数的解析式．

(2)、根据图象说明，当x为何值时， $k_{1} x + b - \frac{k_{2}}{x} < 0$ ．

查看试题解析
22. 如图，平行四边形ABCD的对角线AC、BD相交于点O，AF＝CE.

(1)、求证：△BAE≌△DCF；

(2)、若BD⊥EF，连接DE、BF，判断四边形EBFD的形状，并说明理由.

查看试题解析

23. 某校组织全校学生进行了“航天知识竞赛”，教务处从中随机抽取了n名学生的竞赛成绩（满分100分，每名学生的成绩记为x分）分成如表中四组，并得到如下不完整的频数分布表、频数分布直方图和扇形统计图．根据图中信息，解答下列问题：

分组	频数
A： $60 \leq x < 70$	a
B： $70 \leq x < 80$	18
C： $80 \leq x < 90$	24
D： $90 \leq x \leq 100$	b

(1)、n的值为， a的值为， b的值为；

(2)、请补全频数分布直方图，并计算扇形统计图中表示“C”的圆心角的度数为°；

(3)、竞赛结束后，九年级一班从本班获得优秀

(x \geq 80)

的甲、乙、丙、丁四名同学中随机为抽取两名宣讲航天知识，请用列表或画树状图的方法求恰好抽到甲、乙两名同学的概率．

查看试题解析

24. 某文具店准备购甲、乙两种水笔进行销售，每支进价和利润如表：

甲水笔
乙水笔
每支进价（元）
a
$a + 5$
每支利润（元）
2
3
已知花费400元购进甲水笔的数量和花费800元购进乙水笔的数量相等.

(1)、求甲，乙两种水笔每支进价分别为多少元.

(2)、若该文具店准备拿出2000元全部用来购进这两种水笔，考虑顾客需求，要求购进甲种水笔的数量不超过乙种水笔数量的4倍，问该文具店如何进货能使利润最大，最大利润是多少元.

查看试题解析
25. 如图，在 $△ A B C$ 中， $A B = A C$ ，以 $A B$ 为直径作⊙O交 $B C$ 于点D，过点D作 $D E ⊥ A C$ 于点E．

(1)、求证： $D E$ 是⊙O的切线；

(2)、若 $A B = A C = 6$ ， $t a n ∠ B A C = \frac{3}{4}$ ，求 $D E$ 的长．

查看试题解析
26. 如图，抛物线 $y = - x^{2} + b x + c$ 与x轴相交于A，B两点（点A位于点B的左侧），与y轴相交于点C，M是抛物线的顶点，直线 $x = 1$ 是抛物线的对称轴，且点C的坐标为 $(0 ， 3)$ ．

(1)、求抛物线的解析式；

(2)、已知P为线段 $M B$ 上一个动点，过点P作 $P D ⊥ x$ 轴于点D．若 $P D = m ， △ P C D$ 的面积为S．
①求S与m之间的函数关系式，并写出自变量m的取值范围；
②当S取得最大值时，求点P的坐标．

(3)、在（2）的条件下，在线段 $M B$ 上是否存在点P，使 $△ P C D$ 为等腰三角形？如果存在，直接写出满足条件的点P的坐标；如果不存在，请说明理由．

查看试题解析

	甲水笔	乙水笔
每支进价（元）	a	$a + 5$
每支利润（元）	2	3