四川省达州市渠县2022-2023学年七年级下学期3月月考数学测试题

试卷更新日期：2023-04-04 类型：月考试卷

进入出卷网下载

一、选择题：（每小题3分，共30分，）

1. 若（a^mbⁿ）³=a⁹b¹⁵ ，则m、n的值分别为（）

A、9；5 B、3；5 C、5；3 D、6；12

查看试题解析
2.
如图，点P是直线a外的一点，点A、B、C在直线a上，且PB⊥a，垂足是B，PA⊥PC，则下列不正确的语句是（　　）

A、线段PB的长是点P到直线a的距离 B、PA、PB、PC三条线段中，PB最短 C、线段AC的长是点A到直线PC的距离 D、线段PC的长是点C到直线PA的距离

查看试题解析
3. 新冠病毒（2019-nCoV）是一种新的Sarbecovirus亚属的β冠状病毒，它是一类具有囊膜的正链单股RNA病毒，其遗传物质是所有RNA病毒中最大的，也是自然界广泛存在的一大类病毒.其粒子形状并不规则，直径约60-220nm，平均直径为100nm（纳米）.1米＝10⁹纳米，100nm可以表示为（）米.

A、1×10^-⁶ B、10×10^-⁸ C、1×10^-⁷ D、1×10⁷

查看试题解析
4. 如图，AB∥CD，射线AE交CD于点F，若∠1＝115°，则∠2的度数是（）

A、55° B、65° C、75° D、85°

查看试题解析
5. 运用完全平方公式（a+b）²=a²+2ab+b²计算（x+ $\frac{1}{2}$ ）² ，则公式中的2ab是（）

A、 $\frac{1}{2} x$ B、x C、2x D、4x

查看试题解析
6.
如图，∠AOB的一边OA为平面镜，∠AOB=37°36′，在OB上有一点E，从E点射出一束光线经OA上一点D反射，反射光线DC恰好与OB平行，则∠DEB的度数是（　　）

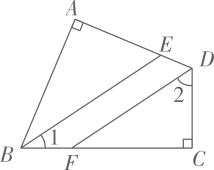
A、75°36′ B、75°12′ C、74°36′ D、74°12′

查看试题解析
7. 小明、小亮、小刚、小颖一起研究一道数学题.如图，已知EF⊥AB，CD⊥AB，
小明说：“如果还知道∠CDG=∠BFE，则能得到∠AGD=∠ACB.”

小亮说：“把小明的已知和结论倒过来，即由∠AGD=∠ACB，

可得到∠CDG=∠BFE.”

小刚说：“∠AGD一定大于∠BFE.”

小颖说：“如果连接GF，则GF一定平行于AB.”

他们四人中，有（）个人的说法是正确的.

A、1 B、2 C、3 D、4

查看试题解析
8. 以下四种沿AB折叠的方法中，不一定能判定纸带两条边线a，b互相平行的是（）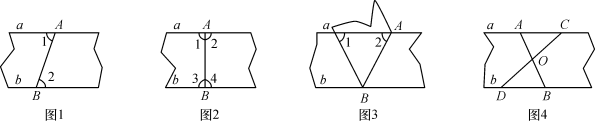

A、如图1，展开后，测得∠1＝∠2 B、如图2，展开后，测得∠1＝∠2，且∠3＝∠4 C、如图3，测得∠1＝∠2 D、如图4，展开后，再沿CD折叠，两条折痕的交点为O，测得OA＝OB，OC＝OD

查看试题解析
9. 如图，根据计算长方形 $ABCD$ 的面积，可以说明下列等式成立的是（）

A、 ${(a + b)}^{2} = a^{2} + 2 ab + b^{2}$ B、 ${(a - b)}^{2} = a^{2} - 2 ab + b^{2}$ C、 $(a + b) (a - b) = a^{2} - b^{2}$ D、 $a (a + b) = a^{2} + ab$

查看试题解析
10. 如图，直线l₁∥l₂ ， ∠CAB＝125°，∠ABD＝85°，则∠1＋∠2等于（）

A、30° B、35° C、36° D、40°

查看试题解析

二、填空题：（每空3分，共18分.）

11. 已知x²ⁿ＝3，则（ $\frac{1}{9}$ x³ⁿ）²•4（-x²）³ⁿ的值是.

查看试题解析
12. 如图，AB∥EF，BC∥DE，则∠E+∠B的度数为.

查看试题解析
13. 某班墙上的“学习园地”是一个长方形，它的面积为6a²－9ab＋3a，已知这个长方形“学习园地”的长为3a，则宽为

查看试题解析
14. 如图，直尺一边AB与量角器的零刻度线CD平行，若量角器的一条刻度线OF的读数为70°，OF与AB交于点E，则∠AEF＝度.

查看试题解析
15. 已知x²+x﹣5=0，则代数式（x﹣1）²﹣x（x﹣3）+（x+2）（x﹣2）的值为．

查看试题解析
16. 一平面内，三条直线两两相交，最多有3个交点；4条直线两两相交，最多有6个交点；5条直线两两相交，最多有10个交点；8条直线两两相交，最多有个交点.

查看试题解析

三、解答题（本大题共10小题，共72分）

17. 计算题：

(1)、 $2 a^{2} (3 a^{2} - 2 a + 1) + 4 a^{3}$

(2)、 $(- 2 x^{2} y + 6 x^{3} y^{4} - 8 x y) \div (- 2 x y)$

(3)、2x³·(－x)²－(－x²)²·(－3x)；

(4)、(2x－y)²·(2x＋y)².

查看试题解析
18. 化简求值：[( 2x－y)(2x＋y)＋y(y－6x)＋x(6y－2)]÷2x，其中x＝-2023

查看试题解析
19. 已知3×9^m×27^m=3²¹ ，求（﹣m²）³÷（m³•m²）的值．

查看试题解析
20. 如图，∠C＝∠1，∠2与∠D互余，BE⊥DF，垂足为G，求证：AB∥CD。

查看试题解析
21. 已知：如图，∠C=∠3，∠2=80°，∠1+∠3=140°，∠A=∠D，求∠B

查看试题解析
22. 如图，直线AB，CD，EF相交于点O.

(1)、写出∠COE的邻补角；

(2)、分别写出∠COE和∠BOE的对顶角；

(3)、若∠BOD＝60°，EF⊥AB，求∠AOF和∠FOC的度数.

查看试题解析
23. 甲、乙两人共同计算一-道整式乘法题：（2x+a）（3x+b）.甲由于把第一个多项式中的“+a”看成了“-a”，得到的结果为6x²-5x-6；乙由于漏抄了第二个多项式中x的系数，得到的结果为2x²+7x+6.

(1)、求正确的a、b的值.

(2)、计算这道乘法题的正确结果.

查看试题解析
24. 如图，已知A，B，C三点在同一条直线上，且AD∥BE，∠3=∠1，试判断BD与CE的位置关系，并说明理由.

查看试题解析
25. 如图，四边形ABCD中，∠A=∠C=90°，BE，DF分别是∠ABC，∠ADC的平分线.

(1)、∠1与∠2有什么关系，为什么？

(2)、BE与DF有什么关系？请说明理由.

查看试题解析
26. 乘法公式的探究及应用.

(1)、如图①，可以求出阴影部分的面积是；（写成两数平方差的形式）

(2)、如图②，若将阴影部分裁剪下来，重新拼成一个长方形，它的宽是，长是，面积是；（写成多项式乘法的形式）

(3)、比较左、右两图的阴影部分面积，可以得到乘法公式：（用式子表达）；

(4)、运用你所得到的公式，计算： $(2 m + n - p) \cdot (2 m - n + p)$ .

查看试题解析