浙江省金华市2023年九年级数学模拟试题

试卷更新日期：2023-04-04 类型：中考模拟

进入出卷网下载

一、选择题（30分）

1. 下列图形中既是轴对称图形又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 如图，二次函数y=ax²+bx+c的图象与x轴相交于（﹣2，0）和（4，0）两点，当函数值y＞0时，自变量x的取值范围是（）

A、x＜﹣2 B、﹣2＜x＜4 C、x＞0 D、x＞4

查看试题解析
3. 如图，四边形ABCD内接于⊙O，已知∠ADC=140°，则∠AOC的大小是（）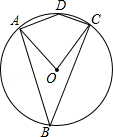

A、80° B、100° C、60° D、40°

查看试题解析
4. 在△ABC中，若∠A，∠B满足|cosA- $\frac{\sqrt{3}}{2}$ |+（1-tanB）²=0，则∠C的大小是（）

A、45° B、60° C、75° D、105°

查看试题解析
5. 如图，⊙O是△ABC的外接圆，⊙O的半径为3，∠A=45°，则 $\overset{⌢}{B C}$ 的长是（）

A、 $\frac{3}{4} π$ B、 $\frac{3}{2} π$ C、 $\frac{45}{2} π$ D、 $\frac{9}{4} π$

查看试题解析
6. 一个多边形的每个外角都等于60°，则这个多边形的边数为（　　）

A、8 B、7 C、6 D、5

查看试题解析
7. 如图，已知⊙O的周长为4π， $\overset{⌢}{A B}$ 的长为π，则图中阴影部分的面积为（）

A、π-2 B、π- $\sqrt{3}$ C、 π D、2

查看试题解析
8. 如图，已知“人字梯”的5个踩档把梯子等分成6份，从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF， $\tan α = \frac{5}{2}$ ，则“人字梯”的顶端离地面的高度AD是（）

A、144cm B、180cm C、240cm D、360cm

查看试题解析
9. 在△ABC中，AB=12 $\sqrt{2}$ ， AC=13，cos∠B= $\frac{\sqrt{2}}{2}$ ，则BC边长为（　　）

A、7 B、8 C、8或17 D、7或17

查看试题解析
10.
如图，已知二次函数y=ax²+bx+c（a≠0）的图象如图所示，给出以下四个结论：①abc=0，②a+b+c＞0，③a＞b，④4ac﹣b²＜0；其中正确的结论有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（24分）

11. 二次函数y=x²﹣4x﹣3的顶点坐标是（，）．

查看试题解析
12. 如图，点P在△ABC的边AC上，请添加一个条件，使△ABP∽△ACB，

查看试题解析
13.
如图，三个小正方形的边长都为1，则图中阴影部分面积的和是（结果保留π）．

查看试题解析
14.
如图，在△ABC中，E，F分别为AB，AC的中点，则△AEF与△ABC的面积之比为 .

查看试题解析
15.
如图，在⊙O中，∠OAB=45°，圆心O到弦AB的距离OE=2cm，则弦AB的长为 cm．

查看试题解析
16. 如图，n+1个边长为2的等边三角形有一条边在同一直线上，设△E₁B₂D₂的面积为S₁ ， △E₂B₃D₃的面积为S₂ ， …，△E_nB_n+1D_n+1的面积为S_n ，则S₁= ， S_n= ．

查看试题解析

三、解答题（66分）

17. 计算： ${(- \frac{1}{3})}^{- 1} + {(2015 - \sqrt{3})}^{0}$ -4sin60°+|- $\sqrt{12}$ |

查看试题解析
18. 如图，△ABC中，D为BC 上一点，∠BAD=∠C，AB=6， BD=4，求CD的长．

查看试题解析
19. 水果种植大户小方，为了吸引更多的顾客，组织了观光采摘游活动．每一位来采摘水果的顾客都有一次抽奖机会：在一只不透明的盒子里有 $A ， B ， C ， D$ 四张外形完全相同的卡片，抽奖时先随机抽出一张卡片，再从盒子中剩下的3张中随机抽取第二张．

(1)、请利用树状图（或列表）的方法，表示前后两次抽得的卡片所有可能的情况；

(2)、如果抽得的两张卡片是同一种水果图片就可获得奖励，那么得到奖励的概率是多少？(A与B同种水果，C与D同种水果。)

查看试题解析
20.
某超市对进货价为10元/千克的某种苹果的销售情况进行统计，发现每天销售量y（千克）与销售价x（元/千克）存在一次函数关系，如图所示．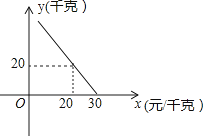

(1)、求y关于x的函数关系式（不要求写出x的取值范围）；

(2)、应怎样确定销售价，使该品种苹果的每天销售利润最大？最大利润是多少？

查看试题解析
21. 如图，已知AB是⊙O的直径，点C、D在⊙O上，点E在⊙O外，∠EAC=∠D=60°．

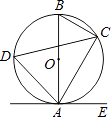(1)、求∠ABC的度数；

(2)、求证：AE是⊙O的切线；

(3)、当BC=4时，求劣弧AC的长．

查看试题解析
22. 如图，为测量某建筑物BC上旗杆AB的高度，小明在距离建筑物BC底部11.4米的点F处，测得视线与水平线夹角∠AED=60°，∠BED=45°．小明的观测点与地面的距离EF为1.6米．

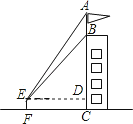(1)、求建筑物BC的高度；

(2)、求旗杆AB的高度（结果精确到0.1米）．
参考数据： $\sqrt{2}$ ≈1.41， $\sqrt{3}$ ≈1.73．

查看试题解析
23. 如图，矩形OABC中，点A，点C分别在x轴，y轴上， D为边BC上的一动点，现把△OCD沿OD对折，C点落在点P处．已知点B的坐标为（ $2 \sqrt{3}$ ， 2）．

(1)、当D点坐标为（2，2）时，求P点的坐标；

(2)、在点D沿BC从点C运动至点B的过程中，设点P经过的路径长度为l，求l的值；

(3)、在点D沿BC从点C运动至点B的过程中，若点P落在同一条直线y=kx＋4上的次数为2次，请直接写出k的取值范围．

查看试题解析
24. 如图，抛物线y=-x²+bx+c经过点B（3，0），点C（0，3），D为抛物线的顶点．

(1)、求抛物线的表达式；

(2)、在抛物线的对称轴上找一点Q，使∠AQC=90°，求点Q的坐标；

(3)、在坐标平面内找一点P，使△OCD与△CBP相似，且∠COD=∠BCP，求出所有点P的坐标．

查看试题解析