浙江省衢州市2023年九年级下学期数学第一次模拟考试题(3月独立作业)
试卷更新日期:2023-04-04 类型:中考模拟
一、选择题(共10小题,每题3分,共30分)
-
1. -2的相反数是( )A、 2 B、-2 C、 D、12. 下列运算正确的是( )A、a2•a4=a6 B、a2+a3=a5 C、(a2)3=a5 D、a2÷a2=a3. 在平面直角坐标系中,点M(m-1,2m)在x轴上,则点M的坐标是( )A、(1,0) B、(-1,0) C、(0,2) D、(0,-1)4. 5个大小相同的正方体搭成的几何体如图所示,其主视图是( )
 A、
A、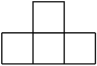 B、
B、 C、
C、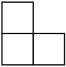 D、
D、 5. 据了解,某定点医院收治的6名“新型冠状肺炎”患者的新冠病毒潜伏期分别为2天,3天,3天,3天,4天,5天,则这6名患者新冠病毒潜伏期的众数为( )A、2天 B、3天 C、4天 D、5天6. 已知在△ABC中,AB=4,BC=7,则边AC的长可能是( )A、2 B、3 C、4 D、117. 不等式组 , 的解集是( )A、x≤-1 B、x>3 C、-3<x≤1 D、-1≤x<38. 一种饮料有两种包装,5大盒、3小盒共装150瓶,2大盒、6小盒共装100瓶,大盒与小盒每盒各装多少瓶?设大盒装x瓶,小盒装y瓶,则可列方程组( )A、 B、 C、 D、9. 如图,小聪用图1中的一副七巧板拼出如图2所示“鸟”,已知正方形ABCD的边长为4,则图2中E,F两点之间的距离为( )
5. 据了解,某定点医院收治的6名“新型冠状肺炎”患者的新冠病毒潜伏期分别为2天,3天,3天,3天,4天,5天,则这6名患者新冠病毒潜伏期的众数为( )A、2天 B、3天 C、4天 D、5天6. 已知在△ABC中,AB=4,BC=7,则边AC的长可能是( )A、2 B、3 C、4 D、117. 不等式组 , 的解集是( )A、x≤-1 B、x>3 C、-3<x≤1 D、-1≤x<38. 一种饮料有两种包装,5大盒、3小盒共装150瓶,2大盒、6小盒共装100瓶,大盒与小盒每盒各装多少瓶?设大盒装x瓶,小盒装y瓶,则可列方程组( )A、 B、 C、 D、9. 如图,小聪用图1中的一副七巧板拼出如图2所示“鸟”,已知正方形ABCD的边长为4,则图2中E,F两点之间的距离为( )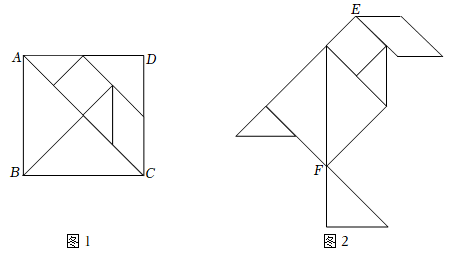 A、 B、2 C、 D、410. 已知二次函数y=ax2-2ax+a+2(a≠0),若-1≤x≤2时,函数的最大值与最小值的差为4,则a的值为( )A、1 B、-1 C、±1 D、无法确定
A、 B、2 C、 D、410. 已知二次函数y=ax2-2ax+a+2(a≠0),若-1≤x≤2时,函数的最大值与最小值的差为4,则a的值为( )A、1 B、-1 C、±1 D、无法确定二、填空题(每小题4分,共24分)
-
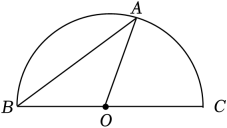
11. 计算:()2=.12. 有一枚质地均匀的骰子,骰子各个面上的点数分别为1~6.任意抛掷这枚骰子,朝上面的点数大于3的概率是 .13. 若分式 有意义,则x的取值范围为 .14. 如图,点A在半圆O上,BC为直径.若∠ABC=30°,BC=3,则的长是 .
 15. 如图,点A,B是反比例函数图象y=(k<0)第二象限上的两点,射线AB交x轴于点C,且B恰好为AC中点,过点B作y轴的平行线,交射线OA于点D,连结CD,若△DCB的面积为3,则k=.
15. 如图,点A,B是反比例函数图象y=(k<0)第二象限上的两点,射线AB交x轴于点C,且B恰好为AC中点,过点B作y轴的平行线,交射线OA于点D,连结CD,若△DCB的面积为3,则k=. 16. 图1是一张可以折叠的小床展开后支撑起来放在地面的示意图,此时点A、B、C在同一直线上,且∠ACD=90°,图2是小床支撑脚CD折叠的示意图,在折叠过程中,△ACD变形为四边形ABC'D',最后折叠形成一条线段BD“.某家装厂设计的折叠床是AB=8cm,BC=16cm,
16. 图1是一张可以折叠的小床展开后支撑起来放在地面的示意图,此时点A、B、C在同一直线上,且∠ACD=90°,图2是小床支撑脚CD折叠的示意图,在折叠过程中,△ACD变形为四边形ABC'D',最后折叠形成一条线段BD“.某家装厂设计的折叠床是AB=8cm,BC=16cm,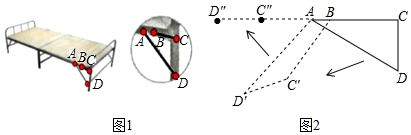
①此时BC''应该是多长;
②折叠时,当AB⊥BC′时,sinD'=.
三、解答题(共8题,共66分)
-
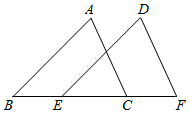
17. 计算:(1)、分解因式:a2-4a+4;(2)、解分式方程:.18. 如图,已知点E、C在线段BF上,BE=CF,AB=DE,AC=DF.求证:∠A=∠D.
 19. 如图,在11×7的长方形网格中,每个小正方形的边长均为1,小正方形的每一个顶点叫做格点,线段DE和三角形ABC的顶点都在格点上.根据下列条件,利用网格点和无刻度的直尺画图并解答相关的问题(保留画图痕迹):
19. 如图,在11×7的长方形网格中,每个小正方形的边长均为1,小正方形的每一个顶点叫做格点,线段DE和三角形ABC的顶点都在格点上.根据下列条件,利用网格点和无刻度的直尺画图并解答相关的问题(保留画图痕迹):
⑴△ABC的面积为 ▲;
⑵在DE的右侧找一点F,使得△DEF与△ABC全等;
⑶画△ABC中BC边上的高AH.
20. 微信圈有篇热传的文章《如果想毁掉一个孩子,就给他一部手机!》.国际上,法国教育部宣布,小学和初中于2018年9月新学期开始,禁止学生使用手机,为了解学生手机使用情况.高新区某学校开展了“手机伴我健康行”的主题活动,学校随机抽取部分学生进行“使用手机的目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,图②的统计图.已知“查资料”的人数是40人.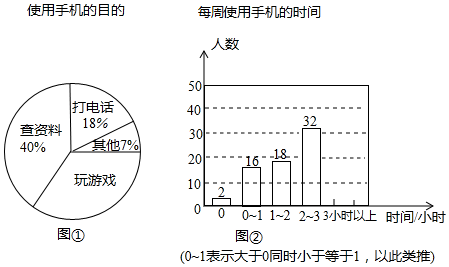 (1)、在这次调查中,一共抽取了 名学生;(2)、在扇形统计图中,“玩游戏”对应的圆心角的度数是 度;(3)、补全条形统计图;(4)、该校共有学生2000人,请估计每周使用手机时间在2小时以上(不含2小时)的人数.21. 如图,⊙O是△ABC的外接圆,AE是⊙O的直径,点B的中点,过点B的切线与AC的延长线交于点D.
(1)、在这次调查中,一共抽取了 名学生;(2)、在扇形统计图中,“玩游戏”对应的圆心角的度数是 度;(3)、补全条形统计图;(4)、该校共有学生2000人,请估计每周使用手机时间在2小时以上(不含2小时)的人数.21. 如图,⊙O是△ABC的外接圆,AE是⊙O的直径,点B的中点,过点B的切线与AC的延长线交于点D.
①求证:BD⊥AD;
②若AC=9,tan∠ABC= , 求⊙O的半径.
22. 如图,小赵和小李相约去农庄游玩.小李从小区甲骑电动车出发.同时,小赵从小区乙开车出发,途中,他去超市买了一些东西后,按原来的速度继续去农庄,小区甲、乙、超市和农庄之间的路程图所示,设他们离小区甲的路程为s(km),出发的时间为t(分).根据图回答问题: (1)、点A的坐标为 , 小赵的开车速度为 km/分;(2)、求线段CB的函数表达式,并写出自变量t的取值范围;(3)、求小赵离开超市后追上小李时,距离农庄多少km?23. 中国在2022年北京冬奥会上向全世界展示了“胸怀大局,自信开放,迎难而上,追求卓越,共创未来”的北京冬奥精神.跳台滑雪是北京冬奥会的比赛项目之一,下图是某跳台滑雪场地的截面示意图.平台AB长1米(即AB=1),平台AB距地面18米.以地面所在直线为x轴,过点B垂直于地面的直线为y轴,取1米为单位长度,建立平面直角坐标系.已知滑道对应的函数为y=x2-4x+c(x≥1).运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落过程中的某位置(忽略空气阻力).设运动员飞出时间为t秒,运动员与点A的竖直距离为h米,运动员与点A的水平距离为l米,经实验表明:h=6t2 , l=vt
(1)、点A的坐标为 , 小赵的开车速度为 km/分;(2)、求线段CB的函数表达式,并写出自变量t的取值范围;(3)、求小赵离开超市后追上小李时,距离农庄多少km?23. 中国在2022年北京冬奥会上向全世界展示了“胸怀大局,自信开放,迎难而上,追求卓越,共创未来”的北京冬奥精神.跳台滑雪是北京冬奥会的比赛项目之一,下图是某跳台滑雪场地的截面示意图.平台AB长1米(即AB=1),平台AB距地面18米.以地面所在直线为x轴,过点B垂直于地面的直线为y轴,取1米为单位长度,建立平面直角坐标系.已知滑道对应的函数为y=x2-4x+c(x≥1).运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落过程中的某位置(忽略空气阻力).设运动员飞出时间为t秒,运动员与点A的竖直距离为h米,运动员与点A的水平距离为l米,经实验表明:h=6t2 , l=vt (1)、求滑道对应的函数表达式;(2)、当v=5,t=1时,通过计算判断运动员此时是否已落在滑道上;(3)、在某一次的试跳中,运动员甲从A处飞出,飞出的路径近似看作函数y=-x2+x+图象的一部分,根据实践可知,若运动员在飞行的过程中,存在飞行的高度与跳台滑道的垂直距离在8~10米的范围内即可成功,请你通过计算说明该运动员此次试跳是否能成功.24. 如图,四边形ABCD是菱形,其中∠ABC=60°,点E在对角线AC上,点F在射线CB上运动,连接EF,作∠FEG=60°,交直线DC于点G.
(1)、求滑道对应的函数表达式;(2)、当v=5,t=1时,通过计算判断运动员此时是否已落在滑道上;(3)、在某一次的试跳中,运动员甲从A处飞出,飞出的路径近似看作函数y=-x2+x+图象的一部分,根据实践可知,若运动员在飞行的过程中,存在飞行的高度与跳台滑道的垂直距离在8~10米的范围内即可成功,请你通过计算说明该运动员此次试跳是否能成功.24. 如图,四边形ABCD是菱形,其中∠ABC=60°,点E在对角线AC上,点F在射线CB上运动,连接EF,作∠FEG=60°,交直线DC于点G.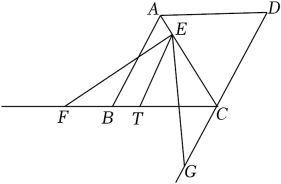 (1)、在线段BC上取一点T,使CE=CT,
(1)、在线段BC上取一点T,使CE=CT,①求证:∠FET=∠GEC
②求证:FT=CG;
(2)、图中AB=7,AE=1.①点F在线段BC上,求△EFG周长的最大值和最小值;
②记点F关于直线AB的轴对称点为点N.若点N落在∠EDC的内部(不含边界),求CF的取值范围.