上海市2023届高三数学模拟试卷

试卷更新日期：2023-04-03 类型：高考模拟

进入出卷网下载

一、填空题

1. 已知 $z = 1 + i$ ，则 $| z - 2 \bar{z} | =$ .

查看试题解析
2. $\vec{a} = (1 ， 2) ， \vec{b} = (- 1 ， t) ， \vec{a} \cdot \vec{b} = 5 ， t =$ .

查看试题解析
3. 双曲线 $x^{2} - {\frac{y}{4}}^{2} = 1$ 的焦点为.

查看试题解析
4. 不等式 $\frac{1}{x + 1} + \frac{1}{x + 3} \geq 0$ 的解集是.

查看试题解析
5. 若 $A = {y ∣ y = e^{x} ， x \in R} ， B = {x ∣ y = l n (2 - x)}$ ，则 $A ∩ B =$ .

查看试题解析
6. $f (x) = c o s (2 x + \frac{π}{2}) + c o s x$ 在 $[0 ， π]$ 的零点为.

查看试题解析
7. 设 $g (x) = f^{'} (x)$ ，则满足 $g^{'} (x)$ 在 $R$ 上恒正的 $f (x)$ 是.（填写序号）
① $f (x) = x^{4} + x^{2}$ ；② $f (x) = s i n x + 2$ ；③ $f (x) = e^{x}$ ；④ $f (x) = - l n (1 + x)$ .

查看试题解析
8. 随机变量 $X$ 的分布列如下列表格所示，其中 $E [X]$ 为 $X$ 的数学期望，则 $E [X - E [X]] =$ .
$X$
1
2
3
4
5
$p$
0.1
$a$
0.2
0.3
0.1

查看试题解析
9. 有五只笔编号1-5，现将其放入编号1-5的笔筒中，且恰有两只笔没有放入与其编号相同的笔筒中，这样的情况有种.

查看试题解析
10. 无穷数列 ${a_{n}}$ 的前 $n$ 项和 $S_{n} \in {a ， a + 3 ， a + 5}$ ，存在正整数 $T$ ，使 $a_{n + T} = a_{n}$ 恒成立，则 $a =$ .

查看试题解析
11. 正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的边长为1，点 $M ､ N$ 分别为 $D D_{1} ､ B C$ 边的中点， $P$ 是侧面 $A D D_{1} A_{1}$ 上动点，若直线 $B M$ 与面 $C_{1} P N$ 的交点位于 $△ C_{1} P N$ 内（包括边界），则所有满足要求的点 $P$ 构成的图形面积为.

查看试题解析
12. $f (x)$ 在 $R$ 上非严格递增，满足 $f (x + 1) = f (x) + 1 ， g (x) = {\begin{array}{l} f (x) ， | x | < 8 \\ f (x - a) ， | x | \geq 8 \end{array}$ ，若存在符合上述要求的函数 $f (x)$ 及实数 $x_{0}$ ，满足 $g (x_{0} + 4) = g (x_{0}) + 1$ ，则 $a$ 的取值范围是.

查看试题解析

二、单选题

13. 已知 $a \neq 0$ ，则“ $a^{3} < a$ ”是“ $\frac{1}{a} > a$ ”的（）条件.

A、充分不必要 B、充要 C、必要不充分 D、既不充分也不必要

查看试题解析
14. 已知两组数据 $x_{1} ， x_{2} ， x_{3} ， x_{4} ， x_{5}$ 和 $y_{1} ， y_{2} ， y_{3} ， y_{4} ， y_{5}$ 的中位数､方差均相同，则两组数据合并为一组数据后，（）

A、中位数一定不变，方差可能变大 B、中位数一定不变，方差可能变小 C、中位数可能改变，方差可能变大 D、中位数可能改变，方差可能变小

查看试题解析
15. 双曲线 $τ$ 的焦点 $(\pm c ， 0)$ ，圆 $C ： (x - c)^{2} + y^{2} = r^{2} (r > 0 ， c > 0)$ ，则（）

A、存在 $c$ ，使对于任意 $r$ ， $C$ 与 $τ$ 至少有一个公共点 B、存在 $c$ ，使对于任意 $r$ ， $C$ 与 $τ$ 至多有两个公共点 C、对于任意 $r$ ，存在 $c$ ，使 $C$ 与 $τ$ 至少有两个公共点 D、对于任意 $r$ ，存在 $c$ ，使 $C$ 与 $τ$ 至多有一个公共点

查看试题解析
16. 设 $x \nabla y = x + y + | x - y | ， x Δ y = x + y - | x - y |$ ，若正实数 $a ， b ， c ， d$ 满足： ${\begin{array}{l} a Δ b < c Δ d \\ a \nabla c < b \nabla d ， \\ b Δ c < a \nabla d \end{array}$ 则下列选项一定正确的是（）

A、 $d > b$ B、 $b > c$ C、 $b Δ c > a$ D、 $d \nabla c > a$

查看试题解析

三、解答题

17. 函数 $f (x) = a^{x} + x (a > 0)$ ，且 $f (1) = e + 1$ .

(1)、判断 $f (x)$ 在 $R$ 上的单调性，并利用单调性的定义证明；

(2)、 $g (x) = f (x) - λ x$ ，且 $g (x)$ 在 $(0 ， + ∞)$ 上有零点，求 $λ$ 的取值范围.

查看试题解析
18. 正四棱锥 $P - A B C D$ 中， $A B = 2$ ， $P O = 3$ ，其中 $O$ 为底面中心， $M$ 为 $P D$ 上靠近 $P$ 的三等分点.

(1)、求四面体 $M - A C P$ 的体积；

(2)、是否存在侧棱 $P B$ 上一点 $N$ ，使面 $C M N$ 与面 $A B C D$ 所成角的正切值为 $\sqrt{2}$ ？若存在，请描述点 $N$ 的位置；若不存在，请说明理由.

查看试题解析
19. 高铁的建设为一个地区的经济发展提供了强大的推进力，也给人们的生活带来极大便捷.以下是2022年开工的雄商高铁线路上某个路段的示意图，其中线段 $A B$ ､ $B C$ 代表山坡，线段 $C D$ 为一段平地.设图中 $A B ､ B C$ 坡的倾角满足 $t a n θ = \frac{7}{24}$ ， $t a n φ = \frac{5}{12} ， A B$ 长 $250 m ， B C$ 长 $182 m ， C D$ 长 $132 m$ .假设该路段的高铁轨道是水平的（与 $C D$ 平行），且端点 $E ､ F$ 分别与 $A ､ D$ 在同一铅垂线上，每隔 $30 m$ 需要建造一个桥墩（不考虑端点 $F$ 建造桥墩）

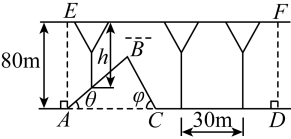(1)、求需要建造的桥墩的个数；

(2)、已知高铁轨道的高度为 $80 m$ ，设计过程中每 $30 m$ 放置一个桥墩，设桥墩高度为 $h$ （单位： $m$ ），单个桥墩的建造成本为 $W = 0.65 h + 5$ （单位：万元），求所有桥墩建造成本总和的最小值.

查看试题解析
20. 已知点 $F$ 是抛物线 $y^{2} = 4 x$ 的焦点，动点 $P$ 在抛物线上，设直线 $l$ 与抛物线交于D､E两点（P､D､E均不重合）.

(1)、若 $l$ 经过点 $F ， | D F | = 3$ ，求 $E$ 点坐标；

(2)、若 $\vec{D F} = \vec{P E}$ ，证明：直线 $D E$ 过定点；

(3)、若 $∠ D P F = ∠ D E F$ 且 $∠ E D P = ∠ E F P$ ，四边形 $D P F E$ 面积为 $\sqrt{2}$ ，求直线 $l$ 的方程.

查看试题解析
21. 数列 ${a_{n}}$ 项数为 $N$ ，我们称 $p$ 为 ${a_{n}}$ 的“映射焦点”，如果 $p$ 满足：① $2 p \in {2 ， 4 ， \dots ， N}$ ；
②对于任意 $n \in [1 ， p]$ ，存在 $k \in [p + 1 ， N]$ ，满足 $a_{n} = a_{k}$ ，并将最小的 $k$ 记作 $k_{n}$ ；

(1)、若 $N = 9$ ，判断 $a_{n} = | n - 5 |$ 时，4是否为映射焦点？5是否为映射焦点？

(2)、若 $N > 40 ， a_{n} = | l o g_{2} n - l o g_{2} 6 |$ 时， $p$ 是映射焦点，证明： $p$ 的最大值为4；

(3)、若 $a_{n} \in N^{*} ， a_{i + 1} - a_{i} \in {- 1 ， 1} (1 \leq i < N) ， n + k_{n} \geq 2 p (1 \leq n \leq p)$ ， $N = 2 p = 100 ， a_{p} = 5$ ，求 $a_{1} + a_{2} + ⋯ + a_{100}$ 的最小值.

查看试题解析

$X$	1	2	3	4	5
$p$	0.1	$a$	0.2	0.3	0.1