陕西省咸阳市2023届高三下学期理数二模试卷
试卷更新日期:2023-04-03 类型:高考模拟
一、单选题
-
1. 已知复数z满足 , 那么( )A、1 B、 C、 D、22. 已知集合 , , 那么( )A、 B、 C、 D、3. 某商场要将单价分别为36元 , 48元 , 72元的3种糖果按3:2:1的比例混合销售,其中混合糖果中每一颗糖果的质量都相等.那么该商场对混合糖果比较合理的定价应为( )A、52元 B、50元 C、48元 D、46元4. 已知m,n是两条不同的直线,α,β是两个不同的平面,有以下四个命题:
①若 , , 则②若 , , 则③若 , , 则④若 , , , 则
其中正确的命题是( )
A、②③ B、②④ C、①③ D、①②5. 函数的大致图象为( )A、 B、
B、 C、
C、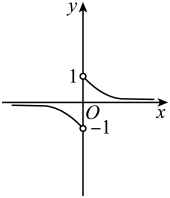 D、
D、 6. 已知函数 , 当时,取得最小值,则的最小值是( )A、 B、 C、 D、7. 数列的前n项和为 , 对一切正整数n,点在函数的图象上,(且),则数列的前n项和为( )A、 B、 C、 D、8. 已知直角三角形ABC, , , , 现将该三角形沿斜边AB旋转一周,则旋转形成的几何体的体积为( )A、12π B、16π C、 D、9. 巴塞尔问题是一个著名的级数问题,这个问题首先由皮耶特罗·门戈利在1644年提出,由莱昂哈德·欧拉在1735年解决.欧拉通过推导得出: . 某同学为了验证欧拉的结论,设计了如图的算法,计算的值来估算,则判断框填入的是( )
6. 已知函数 , 当时,取得最小值,则的最小值是( )A、 B、 C、 D、7. 数列的前n项和为 , 对一切正整数n,点在函数的图象上,(且),则数列的前n项和为( )A、 B、 C、 D、8. 已知直角三角形ABC, , , , 现将该三角形沿斜边AB旋转一周,则旋转形成的几何体的体积为( )A、12π B、16π C、 D、9. 巴塞尔问题是一个著名的级数问题,这个问题首先由皮耶特罗·门戈利在1644年提出,由莱昂哈德·欧拉在1735年解决.欧拉通过推导得出: . 某同学为了验证欧拉的结论,设计了如图的算法,计算的值来估算,则判断框填入的是( ) A、 B、 C、 D、10. 2022年卡塔尔世界杯足球赛落幕,这是历史上首次在卡塔尔和中东国家境内举行、也是第二次在亚洲举行的世界杯足球赛.有甲,乙,丙,丁四个人相互之间进行传球,从甲开始传球,甲等可能地把球传给乙,丙,丁中的任何一个人,以此类推,则经过三次传球后乙只接到一次球的概率为( )A、 B、 C、 D、11. 已知双曲线C: , c是双曲线的半焦距,则当取得最大值时,双曲线的离心率为( )A、 B、 C、 D、12. 已知实数 , …,对任意 , 不等式恒成立,则实数a的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、10. 2022年卡塔尔世界杯足球赛落幕,这是历史上首次在卡塔尔和中东国家境内举行、也是第二次在亚洲举行的世界杯足球赛.有甲,乙,丙,丁四个人相互之间进行传球,从甲开始传球,甲等可能地把球传给乙,丙,丁中的任何一个人,以此类推,则经过三次传球后乙只接到一次球的概率为( )A、 B、 C、 D、11. 已知双曲线C: , c是双曲线的半焦距,则当取得最大值时,双曲线的离心率为( )A、 B、 C、 D、12. 已知实数 , …,对任意 , 不等式恒成立,则实数a的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 的展开式中 的系数为.14. 过抛物线的焦点F的直线l与抛物线交于A,B两点,若l的倾斜角为 , 则线段AB的中点到x轴的距离是 .15. 已知非零向量 , , 满足 , , 的夹角为120°,且 , 则向量 , 的数量积为 .16. 如图,已知在扇形OAB中,半径 , , 圆内切于扇形OAB(圆和OA、OB、弧AB均相切),作圆与圆、OA、OB相切,再作圆与圆、OA、OB相切,以此类推.设圆、圆……的面积依次为 , ……,那么 .

三、解答题
-
17. △ABC的内角A,B,C的对边分别为a,b,c,已知 , .(1)、求;(2)、若 , 求△ABC的周长.18. 如图,直四棱柱的底面是菱形 , , , E,M,N分别是BC, , 的中点.
 (1)、证明:平面;(2)、求二面角的正弦值.19. 2023年1月26日,世界乒乓球职业大联盟(WTT)支线赛多哈站结束,中国队包揽了五个单项冠军,乒乓球单打规则是首先由发球员发球2次,再由接发球员发球2次,两者交替,胜者得1分.在一局比赛中,先得11分的一方为胜方(胜方至少比对方多2分),10平后,先多得2分的一方为胜方,甲、乙两位同学进行乒乓球单打比赛,甲在一次发球中,得1分的概率为 , 乙在一次发球中,得1分的概率为 , 如果在一局比赛中,由乙队员先发球.(1)、甲、乙的比分暂时为8:8,求最终甲以11:9赢得比赛的概率;(2)、求发球3次后,甲的累计得分的分布列及数学期望.20. 椭圆C:的左、右焦点分别为、 , 且椭圆C过点 , 离心率为 .(1)、求椭圆C的方程;(2)、若点是椭圆上任一点,那么椭圆在点M处的切线方程为 . 已知是(1)中椭圆C上除顶点之外的任一点,椭圆C在N点处的切线和过N点垂直于切线的直线分别与y轴交于点P、Q.求证:点P、N、Q、、在同一圆上.
(1)、证明:平面;(2)、求二面角的正弦值.19. 2023年1月26日,世界乒乓球职业大联盟(WTT)支线赛多哈站结束,中国队包揽了五个单项冠军,乒乓球单打规则是首先由发球员发球2次,再由接发球员发球2次,两者交替,胜者得1分.在一局比赛中,先得11分的一方为胜方(胜方至少比对方多2分),10平后,先多得2分的一方为胜方,甲、乙两位同学进行乒乓球单打比赛,甲在一次发球中,得1分的概率为 , 乙在一次发球中,得1分的概率为 , 如果在一局比赛中,由乙队员先发球.(1)、甲、乙的比分暂时为8:8,求最终甲以11:9赢得比赛的概率;(2)、求发球3次后,甲的累计得分的分布列及数学期望.20. 椭圆C:的左、右焦点分别为、 , 且椭圆C过点 , 离心率为 .(1)、求椭圆C的方程;(2)、若点是椭圆上任一点,那么椭圆在点M处的切线方程为 . 已知是(1)中椭圆C上除顶点之外的任一点,椭圆C在N点处的切线和过N点垂直于切线的直线分别与y轴交于点P、Q.求证:点P、N、Q、、在同一圆上.
